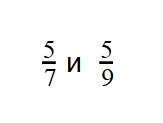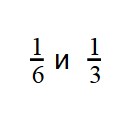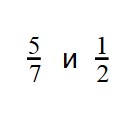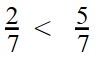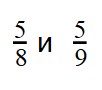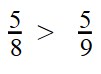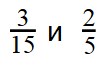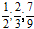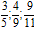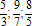Калькулятор дробей
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i n d = i · d + n d
5 3 4 = 5 · 4 + 3 4 = 23 4
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Например, переведем 0.36 в обыкновенную дробь:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
Умножение дробей
Алгоритм действий при умножении двух дробей:
Деление дробей
Алгоритм действий при делении двух дробей:
Сравнение дробей: как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: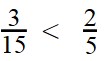
Калькулятор выражений с дробями
Чтобы решить дробное выражение с помощью нашего калькулятора, воспользуйтесь удобной клавиатурой.
Калькулятор на сложение, умножение, вычитание, деление дробей и в том числе с целыми числами. Для того чтобы рассчитать сумму, разность, произведение, частное двух дробей и получить решение, надо ввести числитель, знаменатель, целую часть дроби и выбрать нужную операцию из списка. Чтобы ввести отрицательную дробь, надо поставить знак минус в целой части дроби.
Добро пожаловать на сайт Pocket Teacher
Наш искусственный интеллект решает сложные математические задания за секунды
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
начать
Дроби
Что такое дроби и как их решать
Дробь в математике – это число, являющееся частью единицы или несколькими её частями. То есть если мы хотим указать на половину части целого, то мы пишем обыкновенную дробь ½.
Дробью необязательно мы можем указать часть целого. С помощью дроби мы можем обозначить вообще любое число. Например, дробь 4/2 будет равняться двум, то есть целому числу.
Обыкновенная дробь представляет собой два числа, разделенных горизонтальной чертой – знаком деления. Число, которое располагается над чертой, – числитель, а число под чертой – знаменатель. Знаменатель обозначает количество равных частей, на которое делится целое, а числитель дроби – количество взятых частей данного целого для дальнейшего деления на знаменатель.
Дробь может иметь десятичную форму. Например, обыкновенная дробь 1/10 может обозначаться как 0,1 в десятичной форме. Десятичная форма – это рациональное или иррациональное число, обозначающее дробь. Десятичная форма, может иметь бесконечный вид, например, дробь 1/3 имеет в десятично виде бесконечную форму 0,333333333…
Дроби могут быть правильными и неправильными. Правильной называют такую дробь, у которой числитель меньше знаменателя. В случае если числитель дроби больше знаменателя, она называется неправильной. Дробь, записанная в виде целого числа и правильной дроби называется смешанной. А дробь, которая не имеет целую часть, называется простой дробью. Любую смешанную дробь можно преобразовать в неправильную простую дробь.
Как пользоваться калькулятором дробей?
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Дроби. Вычитание дробей.
Вычитание дробей с одинаковыми знаменателями.
Для нахождения разницы 2х дробей с одинаковыми знаменателями, необходимо вычесть из числителя 1й дроби числитель 2й дроби, а знаменатель обоих дробей оставить не изменяя. Вычитание обыкновенных дробей:
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь, которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:


Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной, единицу переводят к виду неправильной дроби, у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7, т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей – правильной из целого числа (натурального числа) :
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей.
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ), и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители, то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Дроби
Что такое дробь? Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы.
По способу записи дроби делятся на два формата: обыкновенные вида 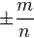
Примеры обыкновенных дробей:
Правильные дроби
Дробь называется правильной, если модуль числителя меньше модуля знаменателя.
Примеры правильных дробей:
Расчеты и формулы дробей онлайн
Неправильные дроби
Дробь называется неправильной, если модуль числителя больше модуля знаменателя.
Примеры неправильных дробей:
Смешанные числа
Запись числа, содержащую целую и дробную части, называют смешанным числом.
Смешанное число можно представить в виде неправильной дроби.
Примеры смешанных чисел:
Десятичные дроби
Бывают задания, когда перевод обыкновенной дроби в десятичную просто необходим.
Десятичная дробь, это дробь которая записывается без знаменателя.
Посмотреть перевод обыкновенной дроби в десятичную можно здесь
Примеры десятичных дробей: 0,1; 0,13; 0,121.