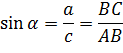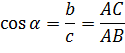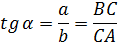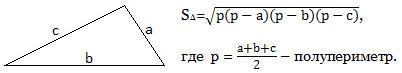Слово Как называется треугольник у которого все стороны равны напишите ответ - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Треугольник. Формулы и свойства треугольников.

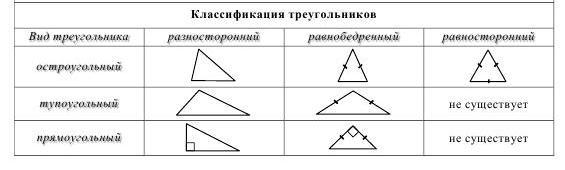
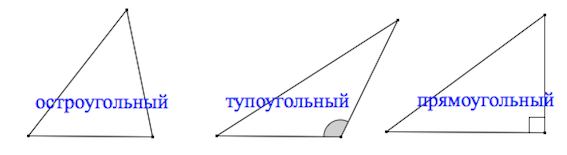
Типы треугольников

По величине углов

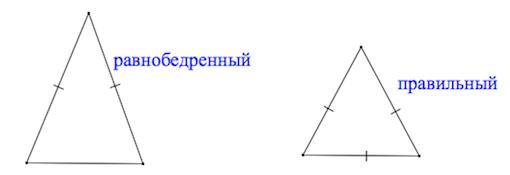
По числу равных сторон

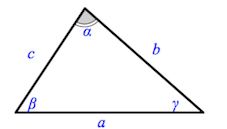
Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

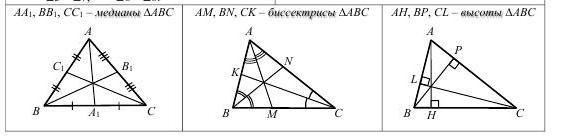
Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

Биссектрисы треугольника

Свойства биссектрис треугольника:

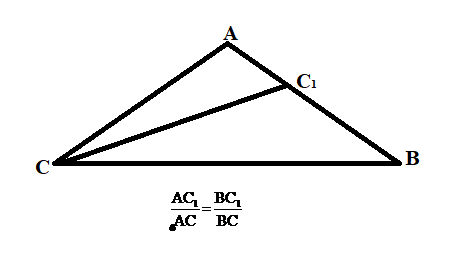
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

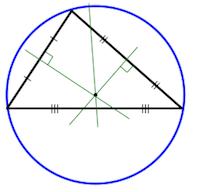
Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

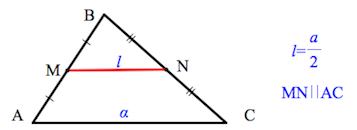
Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

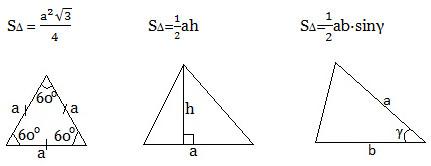
Формулы площади треугольника

Формула Герона

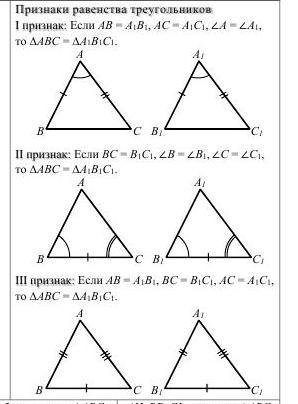
Равенство треугольников

Признаки равенства треугольников

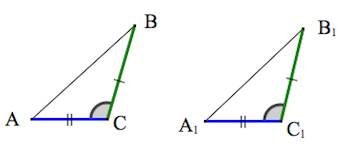
Первый признак равенства треугольников — по двум сторонам и углу между ними

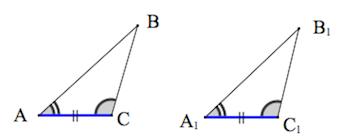
Второй признак равенства треугольников — по стороне и двум прилежащим углам

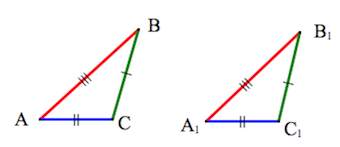
Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Виды треугольников

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

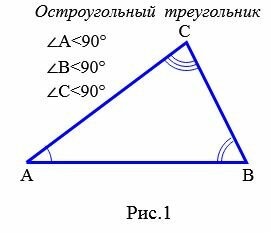Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

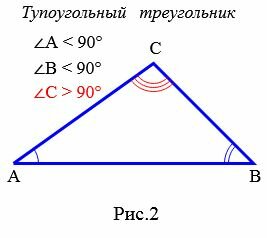Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

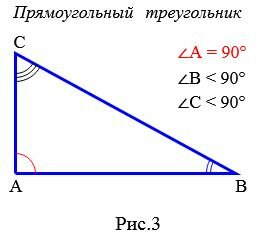Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

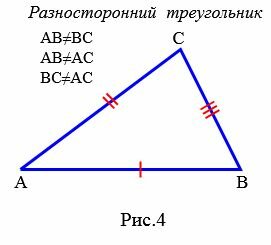Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

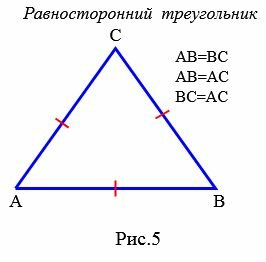Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

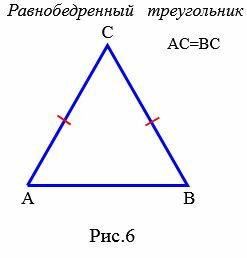В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

Источник

Справочный материал «Треугольники»

Содержимое разработки

а) Прямоугольные, тупоугольные, остроугольные.

Прямоугольный треугольник – треугольник, у которого один угол – прямой, т.е. равный 90°. Остроугольный треугольник – треугольник, у которого все углы острые.

Тупоугольный треугольник – треугольник, у которого два угла острые, а третий – тупой.

По двум сторонам и углу между ними

По стороне и двум прилежащим к ней углам

Медиана треугольника– отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Медианы пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершины.

Медиана делит треугольник на два равновеликих треугольника, площадь каждого из этих двух треугольников равна половине площади данного треугольника.

Биссектриса треугольника – отрезок соединяющий вершину треугольника с противолежащей стороной и делящий угол пополам.

Биссектрисы пересекаются в одной точке.

Точка, лежащая на биссектрисе угла, равноудалена от его сторон.

Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.

Высота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, на которой лежит противоположная сторона.

Высоты или их продолжения пересекаются в одной точке.

Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника..

Средняя линия треугольника параллельна третьей стороне и равна половине этой стороны.

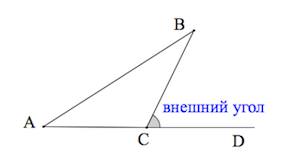
Внешним углом треугольника называется угол, смежный любому углу треугольника.

Его градусная мера равна сумме двух углов треугольника, не смежных с ним.

Соотношение между сторонами и углами треугольника.

против большей стороны лежит больший угол;

против большего угла лежит большая сторона.

каждая сторона треугольника меньше суммы двух других сторон.

Сторону, которая лежит напротив прямого угла, называют гипотенузой.

Катетами называются стороны, которые образуют прямой угол.

Свойства прямоугольного треугольника

Гипотенуза больше любого катета.

Сумма острых углов в прямоугольном треугольнике равна 90°

В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30°.

Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.

Высота h_c, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу.

Каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.

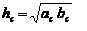
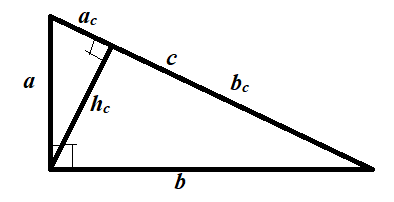
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Признаки прямоугольного треугольника

— Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.

Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.

по гипотенузе и катету,

по катету и острому углу,

по катету и гипотенузе.

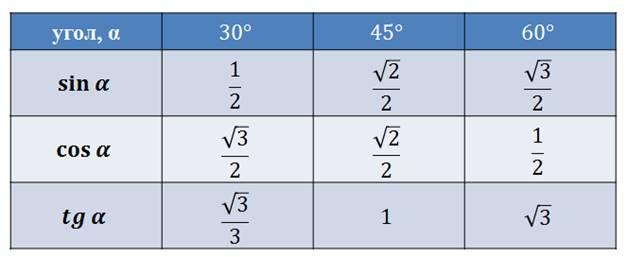
Тригонометрические функции острого угла прямоугольного треугольника

Отношения сторон прямоугольного треугольника не зависят от величин этих сторон, а зависят от величины острых углов прямоугольного треугольника. Для этих отношений были введены специальные названия и обозначения(тригонометрические функции).

синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

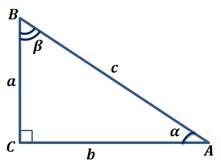
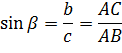
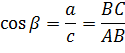
тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Тригонометрические равенства

Основное тригонометрическое тождество

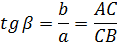
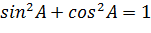
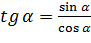
Связь между сторонами и углами в прямоугольном треугольнике

Катет, лежащий против острого угла, равен произведению гипотенузы на синус острого угла.

Катет, прилежащий к острому углу, равен произведению гипотенузы на косинус острого угла.

Катет, лежащий против острого угла, равен произведению второго катета на тангенс острого угла.

Гипотенуза прямоугольного треугольника равна отношению противолежащего катета к синусу острого угла.

Гипотенуза прямоугольного треугольника равна отношению прилежащего катета к косинусу острого угла.

Равнобедренный треугольник – треугольник, у которого две стороны равны.

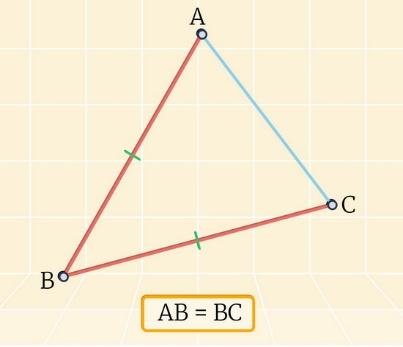
В равнобедренном треугольнике равные стороны называются боковыми, а третья сторона – основанием.

AB и BC – боковые стороны ∆ABC, AC – основание ∆ABC.

Свойства равнобедренного треугольника

В равнобедренном треугольнике углы при основании равны.

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой треугольника.

Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.

Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.

Площадь прямоугольного треугольника.

S_Δ=(½) a∙b, где a и b — катеты или S_Δ=(½) c∙h, где с — гипотенуза, h –высота, проведенная к гипотенузе.

Подобие – это преобразование, при котором расстояние между точками изменяется в одно и то же число раз. Преобразование подобия сохраняет градусные меры углов.

Треугольники называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Признаки подобия треугольников:

1 признак – по двум углам (если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны);

3 признак – по трем сторонам (если все стороны одного треугольника пропорциональны всем сторонам другого треугольника, то такие треугольники подобны).

Если треугольники подобны, то у них соответствующие углы равны, а стороны пропорциональны.

Источник

Треугольник и его виды. Элементы треугольника

Треугольник – это геометрическая фигура, состоящая из трех точек, попарно соединенных между собой отрезками. Точки называются вершинами треугольника, отрезки – сторонами треугольника. Треугольник имеет три вершины и три стороны. Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Внутренние углы треугольника – это углы, образованные его сторонами. Угол А – это угол, образованный сторонами АВ и АС.

Виды треугольников по углам:

Виды треугольников по сторонам:

Элементы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы, которые пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.

Биссектриса – это отрезок, делящий угол треугольника на две равные части. Любой треугольник имеет три биссектрисы, которые пересекаются в одной точке.

Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Любой треугольник имеет три высоты, которые пересекаются в одной точке, называемой ортоцентром треугольника.

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

Серединный перпендикуляр к отрезку – прямая, перпендикулярная к этому отрезку и проходящая через его середину. Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга.

Основные свойства треугольников

Внутренние углы треугольника относятся как 3:7:8. Найдите отношение внешних углов треугольника.

Чему равна градусная мера одного из углов прямоугольного треугольника?

Если в треугольнике один угол больше суммы двух других углов, то он

Если в треугольнике один внешний угол острый, то этот треугольник

Периметр равнобедренного треугольника равен 11 см, а основание равно 3 см. Найдите боковую сторону треугольника.

Источник

Треугольник

Треугольник произвольный

Треугольник – это многоугольник с тремя сторонами (тремя углами).

Виды треугольников :+ показать

Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).

Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).

Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).

Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.

Свойства

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:

(Внешний угол образуется в результате продолжения одной из сторон треугольника).

5. Любая сторона треугольника меньше суммы двух других сторон.

Признаки равенства треугольников

1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.

3. Треугольники равны, если у них соответственно равны три стороны.

Биссектриса, высота, медиана

Здесь подробно о биссектрисе, высоте, медиане треугольника.

Средняя линия треугольника

Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Вписанная окружность

Центр вписанной окружности – точка пересечения биссектрис треугольника.

Описанная окружность

Центр описанной окружности – точка пересечения серединных перпендикуляров.

Соотношение сторон в произвольном треугольнике

Теорема косинусов:

Теорема синусов:

Площадь треугольника

Через сторону и высоту

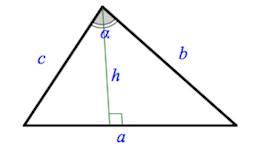
Через две стороны и угол между ними

Через радиус описанной окружности

Через радиус вписанной окружности

, где – полупериметр

, где – полупериметр

Смотрите также площадь треугольника здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉

Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!

В разделе свойства:

Да, не хватало значка «» у А. Спасибо! 😉

Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.

Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение Откуда Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда

спасибо я так и думал а то не могу решить и всё
СПАСИБО!

Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3

Очевидно,
Примите за .
Примените к треугольнику теорему косинусов:

Найдете , далее можно найти угол и из треугольника найти

Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно

Источник