Случайное число
Как и многие другие языки программирования, Python позволяет работать с генераторами случайных значений. С их помощью можно оперативно создавать последовательности из различных чисел или символов, предугадать которые невозможно. Для этой цели в Python применяется встроенная библиотека с множеством методов для управляемой генерации.
Что такое случайные числа?
Случайные числа представляют собой произвольные данные, которые были получены в результате автоматической генерации компьютерной программой. Подобная информация используется во многих видах программного обеспечения, где необходимо иметь дело с непредсказуемыми величинами. Ярким примером тому являются игровые автоматы либо казино, в которых каждый раз генерируется новая выигрышная комбинация чисел. Также данный подход применяется в криптографических целях для создания надежных паролей.
Стоит заметить, что стандартные средства Python не способны предоставлять в программе истинно случайные значения. Они предоставляют псевдо случайную последовательность. Инициализируется она от какого либо случайного числа. То есть если мы будем инициализировать последовательность одним и тем же числом, то она будет каждый раз выдавать одинаковые данные. Чтобы этого не было, для инициализации берется значение системных часов.
Так что обычно используется метод генерации псевдослучайных величин с иницилизацией от системных часов.
Реализации случайных чисел в Python
Язык программирования Python содержит в себе несколько разных модулей, применяемых для генерации псевдослучайных величин. Все они, как правило, используют в своих целях текущее системное время, которое установлено на компьютере. Это гарантирует получение разных последовательностей значений при каждом новом обращении к генератору. Среди инструментов, которые предназначены для работы с псевдослучайными числами, находится довольно обширная библиотека random, а также функции numpy.random и os.urandom.
Особенности их применения:
Наиболее широкое применение получила в Python библиотека random. Поэтому далее мы ее и рассмотрим подробно.
Модуль random
Ниже приведена таблица, где описаны самые главные методы из подключаемого модуля, входящего в состав стандартных библиотек Python. В таблице приведены названия функций, а также доступный перечень параметров с небольшой характеристикой.
| Метод | Характеристика |
| random() | возвращает число в диапазоне от 0 до 1 |
| seed(a) | настаивает генератор на новую последовательность a |
| randint(a, b) | возвращает целое число в диапазоне от a и b |
| randrange(a, b, c) | возвращает целое число в диапазоне от a до b с шагом c |
| uniform(a, b) | возвращает вещественное число в диапазоне от a и b |
| shuffle(a) | перемешивает значения в списке a |
| choice(a) | возвращает случайный элемент из списка a |
| sample(a, b) | возвращает последовательность длиной b из набора a |
| getstate() | возвращает внутреннее состояние генератора |
| setstate(a) | восстанавливает внутреннее состояние генератора a |
| getrandbits(a) | возвращает a случайно сгенерированных бит |
| triangular(a, b, c) | возвращает вещественное число от a до b с распределением c |
Здесь хотелось бы описать функцию seed. Она как раз и применяется для задания инициализирующего числа псевдо случайной последовательности. При вызове seed без параметра, берется значение системного таймера. Эта функция вызывается в конструкторе класса Random.
В примерах мы рассмотрим, как применяются основные функции. А так же в конце рассмотрим как используется SystemRandom.
Примеры
Чтобы воспользоваться возможностями генерации случайных чисел в Python 3, следует произвести импорт библиотеки random, вынеся ее в начало исполняемого файла при помощи ключевого слова import.
Вещественные числа
В модуле есть одноименная функция random. В Python она используется чаще, чем другие функции этого модуля. Функция возвращает вещественное число в промежутке от 0 до 1. В следующем примере демонстрируется создание трех разных переменных a, b и c.
Целые числа
Для получения случайных целых чисел в определенном диапазоне используется функция randint, принимающая два аргумента: минимальное и максимальное значение. Программа, показанная ниже отображает генерацию трех разных значений в промежутке от 0 до 9.
Диапазоны целых
Метод randrange позволяет генерировать целочисленные значения, благодаря работе с тремя параметрами: минимальная и максимальная величина, а также длина шага. Вызвав функцию с одним аргументом, начальная граница получит значение 0, а интервал станет равен 1. Для двух аргументов автоматически инициализируется только длина шага. Работа данного метода с трема разными наборами параметров показана в следующем примере.
Диапазоны вещественных
Сгенерировать вещественное число поможет метод под названием uniform. Он принимает всего два аргумента, обозначающих минимальное и максимальное значения. Демонстрация его работы располагается в следующем примере кода, где создаются переменные a, b и c.
Использование в генераторах
Возможности генерации псевдослучайных чисел можно использовать и для создания последовательностей. В следующем фрагменте кода создается набор чисел при помощи генератора списка со случайным наполнением и длиной. Как можно заметить, в данном примере функция randint вызывается дважды: для каждого элемента и размера списка.
Перемешивание
Метод shuffle дает возможность перемешать содержимое уже созданного списка. Таким образом, все его элементы будут находиться в абсолютно случайном порядке. Пример, где отображается работа этой функции со списком a из 10 значений, располагается дальше.
Случайный элемент списка
При помощи функции choice можно извлечь случайный элемент из существующего набора данных. В следующем примере переменная b получает некое целое число из списка a.
Несколько элементов списка
Извлечь из последовательности данных можно не только один элемент, но и целый набор значений. Функция sample позволит получить абсолютно новый список чисел из случайных компонентов уже существующего списка. В качестве первого аргумента необходимо ввести исходную последовательность, а на месте второго указать желаемую длину нового массива.
Генерация букв
Возможности стандартной библиотеки позволяют генерировать не только числа, но и буквы. В следующем примере показывается инициализация трех разных переменных случайными символами латиницы. Для этого необходимо произвести импортирование модуля string, а затем воспользоваться списком letters, который включает все буквы английского алфавита.
Как можно заметить, отображаются буквы в разном регистре. Для того чтобы преобразовать их к общему виду, рекомендуется вызвать стандартные строковые методы upper или lower.
SystemRandom
Как уже говорилось ранее, SystemRandom основана на os.urandom. Она выдает так же псевдослучайные данные, но они зависят дополнительно и от операционной системы. Результаты используются в криптографии. Есть недостаток — то что функции SystemRandom отрабатывают в несколько раз дольше. Рассмотрим пример использования:
Заключение
Таким образом, язык программирования Python содержит массу встроенных методов для генерации и обработки случайных значений. Пользоваться ими можно при помощи разных библиотек, входящих в стандартный набор инструментов платформы. Благодаря данным функциям можно задавать различные условия, а также ограничения для своих генераторов.
Python 3: Генерация случайных чисел (модуль random)¶
«Генерация случайных чисел слишком важна, чтобы оставлять её на волю случая»
Python порождает случайные числа на основе формулы, так что они не на самом деле случайные, а, как говорят, псевдослучайные [1]. Этот способ удобен для большинства приложений (кроме онлайновых казино) [2].
| [1] | Википедия: Генератор псевдослучайных чисел |
| [2] | Доусон М. Программируем на Python. — СПб.: Питер, 2014. — 416 с.: ил. — 3-е изд |
Модуль random позволяет генерировать случайные числа. Прежде чем использовать модуль, необходимо подключить его с помощью инструкции:
random.random¶
random.random() — возвращает псевдослучайное число от 0.0 до 1.0
random.seed¶
random.seed( ) — настраивает генератор случайных чисел на новую последовательность. По умолчанию используется системное время. Если значение параметра будет одиноким, то генерируется одинокое число:
random.uniform¶
random.randint¶
random.choince¶
random.choince( ) — возвращает случайный элемент из любой последовательности (строки, списка, кортежа):
random.randrange¶
random.shuffle¶
random.shuffle( ) — перемешивает последовательность (изменяется сама последовательность). Поэтому функция не работает для неизменяемых объектов.
Вероятностные распределения¶
random.expovariate(lambd) — экспоненциальное распределение. lambd равен 1/среднее желаемое. Lambd должен быть отличным от нуля. Возвращаемые значения от 0 до плюс бесконечности, если lambd положительно, и от минус бесконечности до 0, если lambd отрицательный.
random.gauss(значение, стандартное отклонение) — распределение Гаусса.
random.normalvariate(mu, sigma) — нормальное распределение. mu — среднее значение, sigma — стандартное отклонение.
random.vonmisesvariate(mu, kappa) — mu — средний угол, выраженный в радианах от 0 до 2π, и kappa — параметр концентрации, который должен быть больше или равен нулю. Если каппа равна нулю, это распределение сводится к случайному углу в диапазоне от 0 до 2π.
random.paretovariate(alpha) — распределение Парето.
random.weibullvariate(alpha, beta) — распределение Вейбулла.
Примеры¶
Генерация произвольного пароля¶
Хороший пароль должен быть произвольным и состоять минимум из 6 символов, в нём должны быть цифры, строчные и прописные буквы. Приготовить такой пароль можно по следующему рецепту:
Этот же скрипт можно записать всего в две строки:
Данная команда является краткой записью цикла for, вместо неё можно было написать так:
Данный цикл повторяется 12 раз и на каждом круге добавляет к строке psw произвольно выбранный элемент из списка.
Random Python
Каждый человек ежедневно сталкивается со случайностью. Википедия нам говорит: случайность — это результат маловероятного или непредсказуемого события. Непредсказуемого. Стоит отметить, что, чем сложнее система, тем ниже возможность прогнозировать (предсказывать) её будущие состояния. Мир сложен и именно по-этому случайность встречается столь часто. Можно сказать, что случайностью мы называем все события, которые не можем предугадать. Таким образом, разговор о случайном – это разговор о нехватке информации. Но эту нехватку человек научился использовать себе на пользу. К примеру, случайные величина широко применяются в криптографии.
В языке Python есть удобные инструменты для работы со случайными значениями. Речь о модуле стандартной библиотеки под названием random (и не только о нём). Давайте знакомиться!
Как использовать модуль random в Python
Для начала модуль надо импортировать.
Python функции модуля random
Случайное целое число — randint() функция random
Самое частое применение данного модуля — генерация случайных чисел. Самая популярная функция для этого — randint().
Она возвращает случайное целое число, лежащее в диапазоне, указанном в параметрах функции. Оба аргумента обязательны и должны быть целыми числами.
Генерация случайного целого числа — randrange()
Функция randrange() используется для генерации случайного целого числа в пределах заданного диапазона. Отличие от randint() заключается в том, что здесь есть третий параметр – шаг, по умолчанию равный единице.
Выбор случайного элемента из списка choice()
Вы играли в детстве в «считалочки»? Эники-беники… Вот этим и занимается random.choice(): функция возвращает один случайный элемент последовательности.
Функция sample()
random.sample() применяется, когда надо выбрать несколько элементов из заданной коллекции. Она возвращает список уникальных элементов, выбранных из исходной последовательности. Количество элементов, которое вернёт функция, задаётся аргументом k.
Случайные элементы из списка — choices()
random.choices делает то же, что и random.sample(), но элементы, которые она возвращает, могут быть не уникальными.
Генератор псевдослучайных чисел — seed()
Метод seed() используется для инициализации генератора псевдослучайных чисел в Python. Вот что это означает: для генерации псевдослучайных чисел необходимо какое-то исходное число и именно это число можно установить данным методом. Если значение seed не установлено, тогда система будет отталкиваться от текущего времени.
Перемешивание данных — shuffle()
Метод random.shuffle() применяется для расстановки элементов последовательности в случайном порядке. Представьте коробку в которой лежат какие-то предметы. Встряхните её ?
Генерации числа с плавающей запятой — uniform()
random.uniform() похожа на randint(), но применяется для генерации числа с плавающей запятой в указанном диапазоне.
Функция triangular()
Функция random.triangular() позволяет управлять вероятностью – она возвращает случайное число с плавающей запятой, которое соответствует заданному диапазону, а также уточняющему значению mode. Этот параметр дает возможность взвешивать возможный результат ближе к одному из двух других значений параметров. По умолчанию он находится посередине диапазона.
Криптографическая зашита генератора случайных данных
Случайные числа, полученные при помощи модуля random в Питоне, не являются криптографически устойчивыми. Это означает, что криптоанализ позволяет предсказать какое число будет сгенерировано следующим. Попробуем исправить ситуацию.
Его зачастую следует использовать вместо генератора псевдослучайных чисел по умолчанию в модуле random, который предназначен для моделирования и симуляции, а не безопасности или криптографии.
Numpy.random — Генератор псевдослучайных чисел
Самый простой способ задать массив со случайными элементами — использовать функцию sample (или random, или random_sample, или ranf — это всё одна и та же функция).
Без аргументов возвращает просто число в промежутке [0, 1), с одним целым числом — одномерный массив, с кортежем — массив с размерами, указанными в кортеже (все числа — из промежутка [0, 1)).
Генерация случайного n-мерного массива вещественных чисел
numpy.random.rand()применяется для генерации массива случайных вещественных чисел в пределах заданного диапазона.
Также можно генерировать числа согласно различным распределениям (Гаусса, Парето и другие). Чаще всего нужно равномерное распределение, которое можно получить с помощь функции uniform.
Для начала необходимо установить Numpy.
Генерация случайного n-мерного массива целых чисел
С помощью функции randint или random_integers можно создать массив из целых чисел. Аргументы: low, high, size: от какого, до какого числа (randint не включает в себя это число, а random_integers включает), и size — размеры массива.
Выбор случайного элемента из массива чисел или последовательности
Функция NumPy random.choice() используется для получения случайных выборок одномерного массива, который возвращается как случайные выборки массива NumPy. Эта функция генерирует случайные выборки, которые обычно используются в статистике данных, анализе данных, полях, связанных с данными, а также может использоваться в машинном обучении, байесовской статистике и т. д.
Генерация случайных универсальных уникальных ID
Универсальные уникальные идентификаторы, также известные как UUID, — это 128-битные числа, используемые для однозначной идентификации информации в компьютерных системах. UUID могут использоваться для обозначения широкого спектра элементов, включая документы, объекты, сеансы, токены, сущности и т. Д. Их также можно использовать в качестве ключей базы данных.
Эта библиотека генерирует уникальные идентификаторы на основе системного времени и сетевого адреса компьютера. Объект UUID неизменяем и содержит некоторые функции для создания различных уникальных идентификаторов.
UUID состоит из пяти компонентов, каждый из которых имеет фиксированную длину. Символ дефиса разделяет каждый компонент. Мы можем представить UUID в формате «8-4-4-4-12», где каждая из цифр представляет длину в шестнадцатеричном формате.
UUID Python, сгенерированный с помощью функции uuid4(), создается с использованием истинно случайного или псевдослучайного генератора. Поэтому вероятность повторения двух гуидов невелика. Когда UUID необходимо сгенерировать на отдельных машинах или мы хотим сгенерировать безопасные UUID, используйте UUID4 (). Он также используется для генерации криптографически безопасных случайных чисел.
Готовимся к собеседованию: случайные числа в Python
Случайность управляет миром, а вы будете управлять случайностью. С помощью Python, конечно.
Чтобы имитировать бросок кубика в игре или предсказать загруженность интернет-ресурса, нужны случайные числа.
Мы разобрали самые популярные вопросы о случайных числах в Python с собеседований. Чаще всего для ответа достаточно написать код и кратко его прокомментировать. Да пребудет с вами Великий Рандом!
Главное, что нужно помнить
С некоторых пор утверждает, что он data scientist. В предыдущих сезонах выдавал себя за математика, звукорежиссёра, радиоведущего, переводчика, писателя. Кандидат наук, но не точных. Бесстрашно пишет о Data Science и программировании на Python.
Вопрос 1. Что такое случайные числа?
Что нужно помнить: случайные числа — это математическое понятие, и их не следует путать с обыденными, произвольными числами. Случайное число в математике и программировании — это:
Другими словами, существует закон или правило, которое называется «функцией распределения» или просто «распределением». И это самое распределение «раздаёт» каждому числу из диапазона определённую вероятность выпадения.
В качестве диапазона значений математикам и программистам привычнее всего использовать диапазон действительных чисел от 0 до 1, но это могут быть и целые числа от 1 до 6, как в игральном кубике, или от 100 до 1 000 000 — и так далее. Главное, что и распределение, и диапазон известны заранее, а само число нет.
Итого: случайные числа — это искусственно полученная последовательность чисел из определённого диапазона, которая подчиняется одному из законов распределения случайной величины.
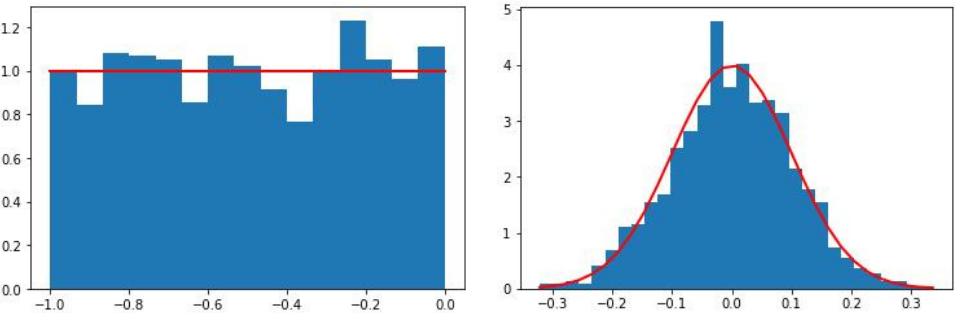
Распределения бывают разные. Так, равномерное распределение — это когда любое значение из диапазона имеет одну и ту же вероятность выпадения (как у игрального кубика или монетки). Если же распределение, например, нормальное (гауссиана), то чаще выпадают числа из середины диапазона. Есть даже таблица — она поможет выбрать подходящее распределение.
Вопрос 2. Как получить случайные числа в Python?
Основных способов два: с помощью «родной» библиотеки random и с помощью модуля numpy.random из библиотеки numpy.
Прежде чем интервьюер придерётся, не забудьте сказать, что и random, и numpy.random — генераторы псевдослучайных чисел (о них ниже). Истинно случайные числа можно получить, например, c сайта Random.Org: там они генерируются с помощью атмосферного шума.
Библиотека random имеет меньший объём, чем numpy.random, и проще в использовании. Зато numpy.random содержит дополнительные распределения для научных вычислений, а также функции для генерирования целых массивов случайных данных.
В первой строчке мы импортировали default_rng — это «генератор генераторов» случайных массивов из модуля numpy.random. Во второй — создали экземпляр такого генератора и присвоили ему имя rng. В третьей использовали его метод standard_normal, чтобы получить numpy-массив из 10 случайных чисел, и записали массив в переменную vals.
Вопрос 3. Псевдослучайные числа
Псевдослучайные числа — это, если очень упрощать, последовательность чисел, которая только выглядит случайной, а на самом деле каждое число в ней определяется алгоритмом, то есть вычисляется. Псевдослучайные последовательности цикличны: через какой-то период все числа повторяются в точности в том же порядке.
Библиотека random и модуль numpy.random содержат в себе генератор не истинно случайных, а именно псевдослучайных чисел.
Генерировать истинно случайные числа дорого и сложно. Основная трудность состоит в том, чтобы гарантировать отсутствие какого-либо цикла, правила или алгоритма. Чаще всего истинно случайные числа берут из физического мира: шумов атмосферы, детекторов частиц, колебаний электрического тока или из космического излучения.
То, что псевдослучайная последовательность, в отличие от истинно случайной, воспроизводима, очень удобно для практических задач: часто нужно подать на вход ту же самую последовательность второй раз, чтобы посмотреть, как работает программа после добавления новых фич.
Наиболее популярный современный алгоритм генерирования псевдослучайных чисел разработан в 1997 году и носит красивое название «Вихрь Мерсенна». Он используется и в Python. Последовательность чисел, порождённая им, статистически неотличима от истинно случайной и имеет период, равный числу с шестью тысячами знаков. Этого хватает для задач симуляции и моделирования, но с точки зрения криптографии такая последовательность всё равно небезопасна: для успешной атаки достаточно иметь сравнительно небольшую сгенерированную этим генератором последовательность.
Вопрос 4. Как повторить случайную последовательность?
Истинно случайную последовательность повторить невозможно. Но для повторения псевдослучайных чисел в обеих основных библиотеках — random и numpy.random есть функция seed (), которая отвечает за инициализацию («посев») последовательности.
Передавая аргумент 42 в функцию seed(), мы указываем конкретное место в псевдослучайной последовательности, поэтому команда random.random() в третьей и последней строках выдаёт одинаковое число — оно идёт первым после точки, помеченной как seed (42).
В seed() можно передать целые и дробные числа, а также строки и кортежи. Если оставить скобки пустыми, то в качестве аргумента seed() возьмёт текущее системное время.
Аналогичная функция есть в модуле numpy.random:
Вопрос 5. Красные и зелёные шары
Часто на собеседованиях просят написать программу, связанную с вероятностями. Например, код для численной проверки ответа к задачке «Какова вероятность вытащить зелёный шар из мешка, в котором 1 зелёный и 4 красных шара».
(Ответ ⅕ = 0,2).
Иными словами, если 100 раз вынимать шар из мешка, возвращая его обратно, количество выпадения зелёных шаров должно приближаться к 20. Вариант кода для проверки:
Функция random.choice() случайным образом выбирает значение из заданного диапазона — списка из одного « green» и четырёх « red». Код выведет количество зелёных шаров после 100 попыток.
Вопрос 6. Нечестная монетка
Другой вариант: предположим, у нас есть так называемая «нечестная» монетка, где орёл ( H, «heads») и решка ( T, «tails») выпадают не с вероятностью ½, как положено, а по-другому: орёл с вероятностью p(H) = 0,2, а решка, соответственно, p(T) = 0,8.
Тогда код для проверки будет выглядеть примерно так:
Здесь используется другая функция, choices, в которую вместе со списком значений можно в параметре weights передавать вероятности их выпадения.
Код выведет количество выпавших орлов после 10 000 бросков.
К слову: задачи на нечестные монетки, наряду с поиском n-ного числа Фибоначчи и нахождением угла между часовой и минутной стрелками, кочуют из одного собеседования в другое уже не первый десяток лет. Есть вероятность, что одна из них попадётся и вам.
Вопрос 7. Проиллюстрируйте закон больших чисел
Закон больших чисел (ЗБЧ) говорит, что при увеличении количества попыток случайная величина стремится к своему математическому ожиданию — всё усредняется. Подробнее об этом можно прочитать в нашей статье об основах математики для Data Science.
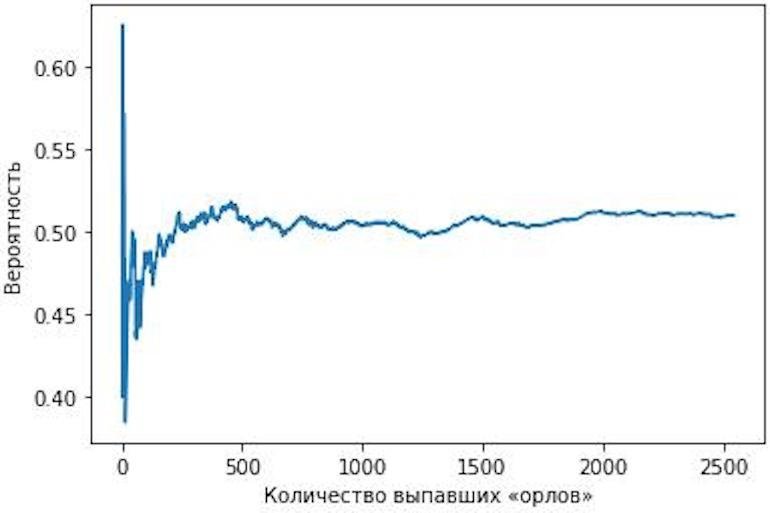
Код для иллюстрации ЗБЧ на примере честной монетки выглядит так:
Вначале мы импортировали уже знакомый нам модуль random и модуль matplotlib.plt — он нужен для рисования простых графиков. После этого определили переменные: общее количество бросков ( total_flips), список из значений вероятностей ( numerical_probability), количество выпавших орлов ( H_count).
Теперь в цикле мы 5 000 раз «подбрасываем» монетку. Если выпадает орёл (« H»), то делим текущее количество выпавших орлов на текущее количество бросков и добавляем итоговое значение в конец списка numerical_probability. В конце рисуем график.
Чем больше бросков, тем ближе к 0,5 вероятность выпадения орла. Всё, как и предсказывает закон больших чисел.
Вопрос 8. Где применяются случайные числа?
В логистике: при расчётах страховых запасов товара — чтобы склад внезапно не опустел или, наоборот, не пришлось держать избыток товара слишком долго. Принято считать, что поведение покупателей случайно и подчиняется одной из разновидностей нормального распределения. В особо запущенных случаях считается случайным даже поведение поставщиков.
В науке: с помощью метода Монте-Карло учёные моделируют поведение частиц во фрактальном окружении в трёхмерном пространстве. Метод Монте-Карло основан на использовании большого количества генерируемых случайных чисел.
В микроэлектронике: броуновское движение частиц играет важную роль в формировании пористости плёночного покрытия полупроводников при напылении его на поверхность. Просчитать это на компьютере гораздо дешевле, чем экспериментировать с реальным покрытием, поэтому сначала его рассчитывают, а потом запускают в производство.
В криптографии: для генерации шифровальных ключей. Здесь становится особенно важным различие между псевдослучайными и истинно случайными числами.
Случайности не случайны
А чтобы никакая псевдослучайность не помешала вам успешно пройти собеседование, приходите в наш Шаолинь на курс «Профессия Python-разработчик». Вы изучите random, numpy и ещё много приёмов пайтонического кунг-фу, а мы поможем с наставниками, единомышленниками и, конечно, с трудоустройством.
Персонаж мультфильма «Кунг-фу Панда», старая мудрая черепаха, учитель и основоположник кунг-фу.