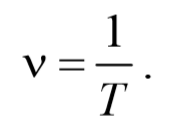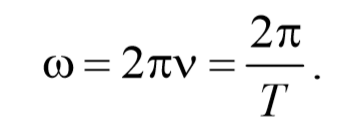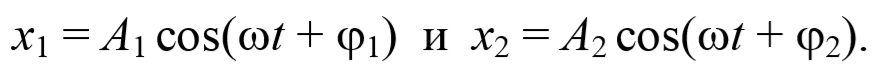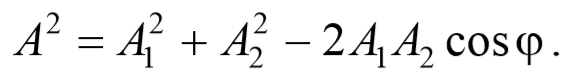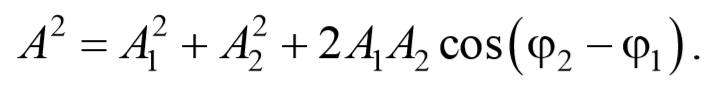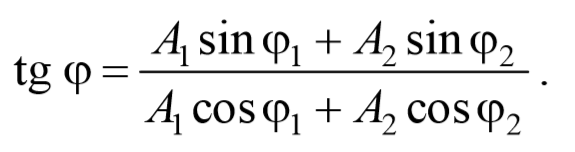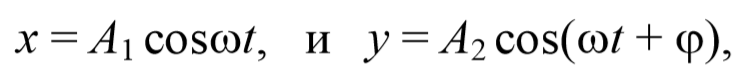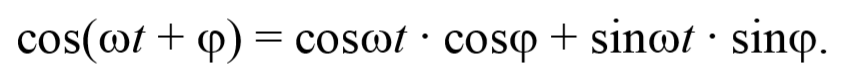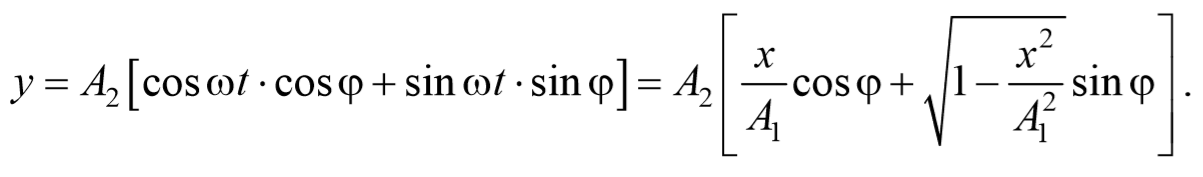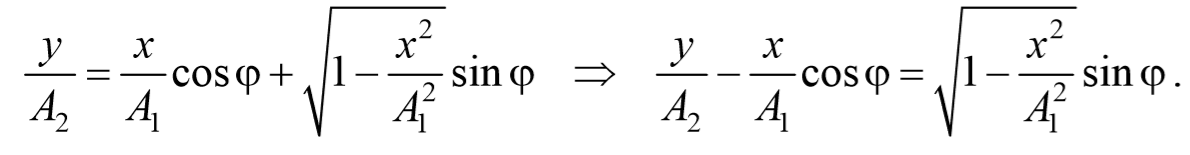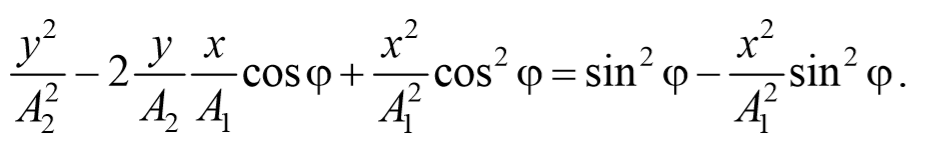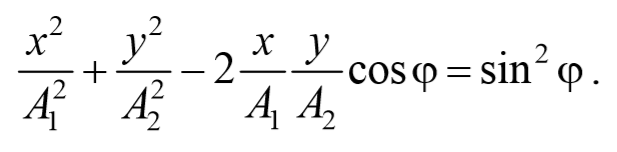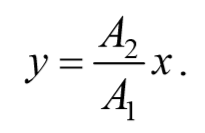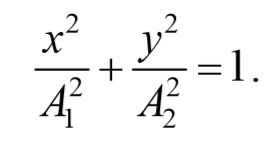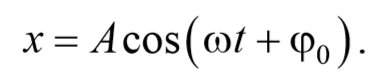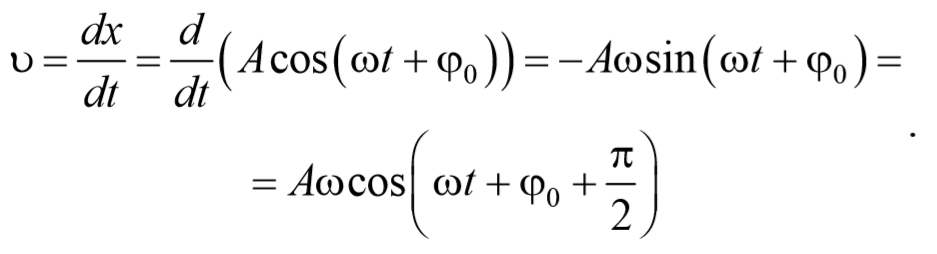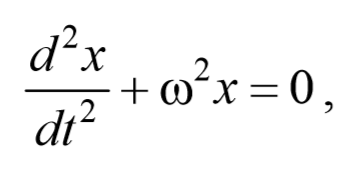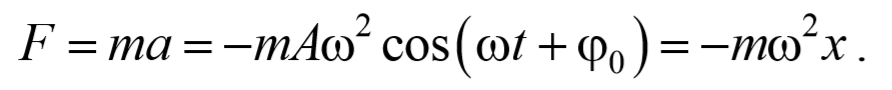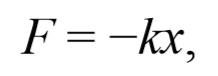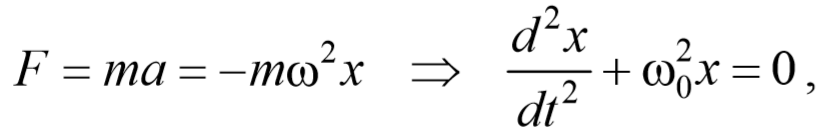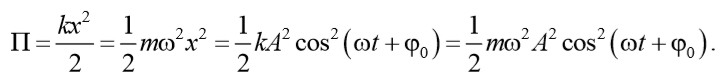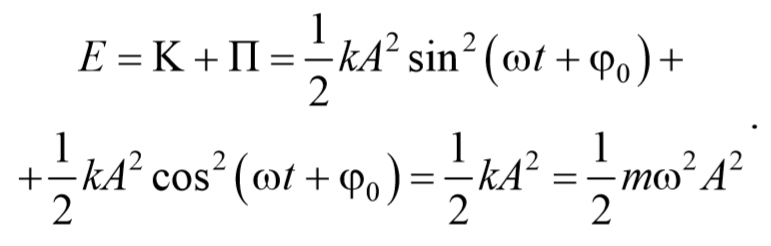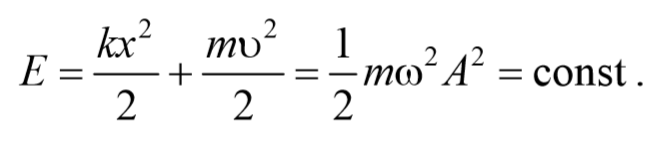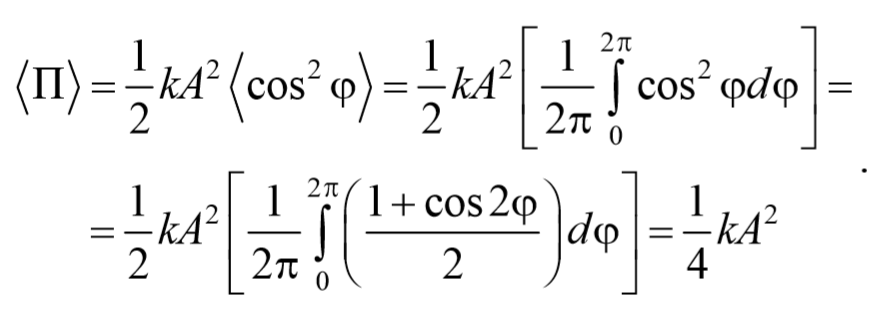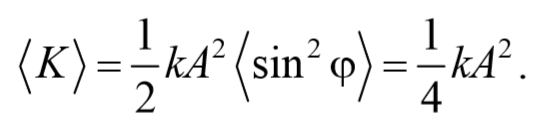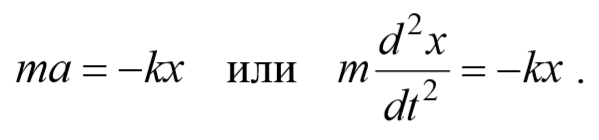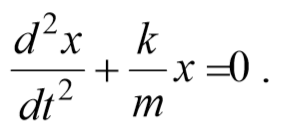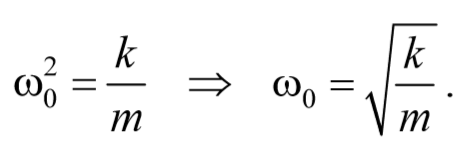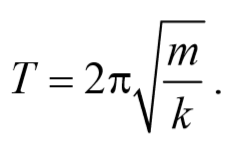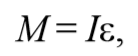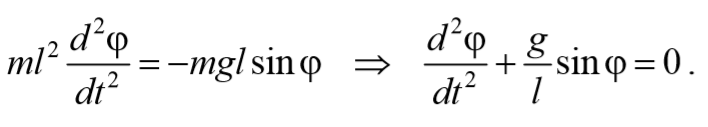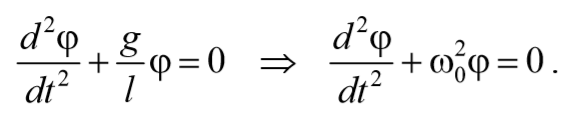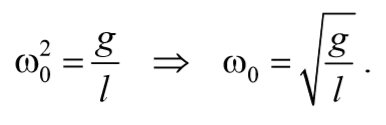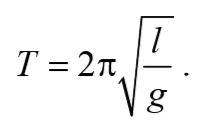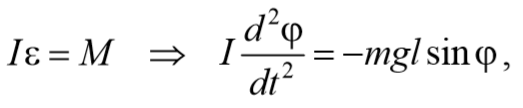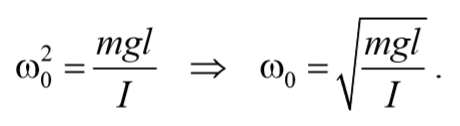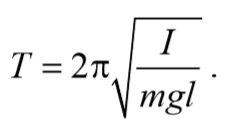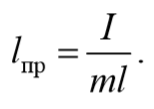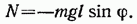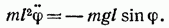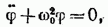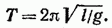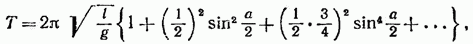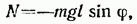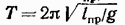Слово Как написать дифференциальное уравнение колебания - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Дифференциальное уравнение гармонических колебаний и его решение

Гармонические колебания

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

Колебаниями называют движения или изменения состояния, повторяющиеся через определенные промежутки времени.

Простейшим видом колебательного движения являются гармонические колебания, когда колеблющаяся величина изменяется со временем по закону синуса или косинуса.

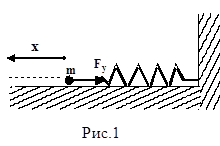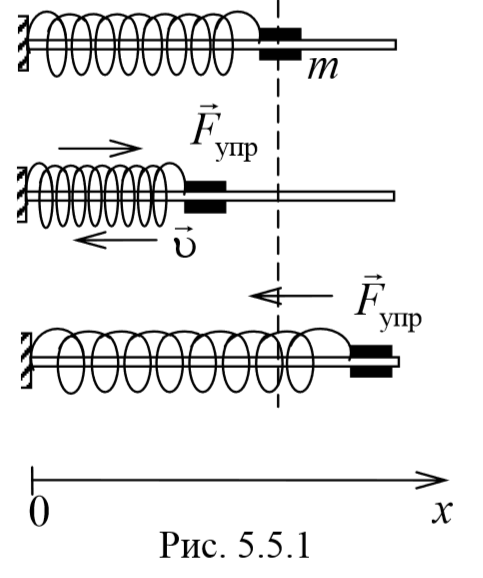
Знак “минус” указывает на противоположность направлений смещения и действия силы упругости.

Чтобы установить характер движения, т.е. зависимость х = f(t), запишем для этого случая дифференциальное уравнение, считая что в рассматриваемой системе движение определяется только наличием силы упругости:

. (1)

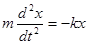
Разделим левую и правую части уравнения (1) на mи обозначим отношение положительных величин k и m через w₀ 2 :

или. (2)

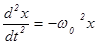
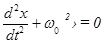
Решение дифференциального уравнения (2) имеет вид:

Зависимость скорости (v) движения материальной точки от времени при гармоническом колебаниинайдем, взяв производную по времени от формулы (3):

(4)

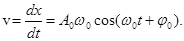
Из сравнения выражений (3) и (4) видно, что смещение и скорость гармонического колебания различаются по фазе на p /2: скорость максимальна при прохождении точкой положения равновесия (смещение равно нулю), наоборот, при максимальном смещении (равном амплитуде) скорость равна нулю.

Выражение для ускорения получается дифференцированием формулы (4):

(5)

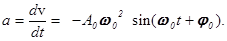
Из формул (3) и (5) следует, что смещение и ускорение изменяются в противофазе.

Источник

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.1. Свободные гармонические колебания и их характеристики.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

За период система совершает одно полное колебание.

6) Фаза колебаний ωt + φ₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

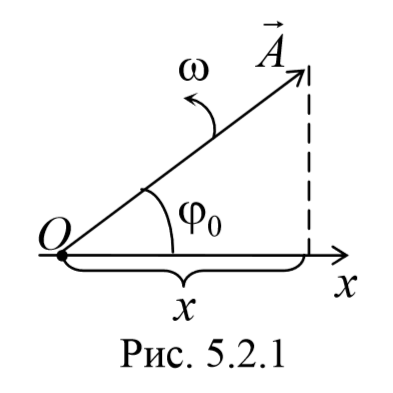
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

1. Сложение одинаково направленных гармонических колебаний.

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

где φ − разность фаз обоих колебаний.

Перепишем это уравнение в следующем виде

После преобразования, получим

Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

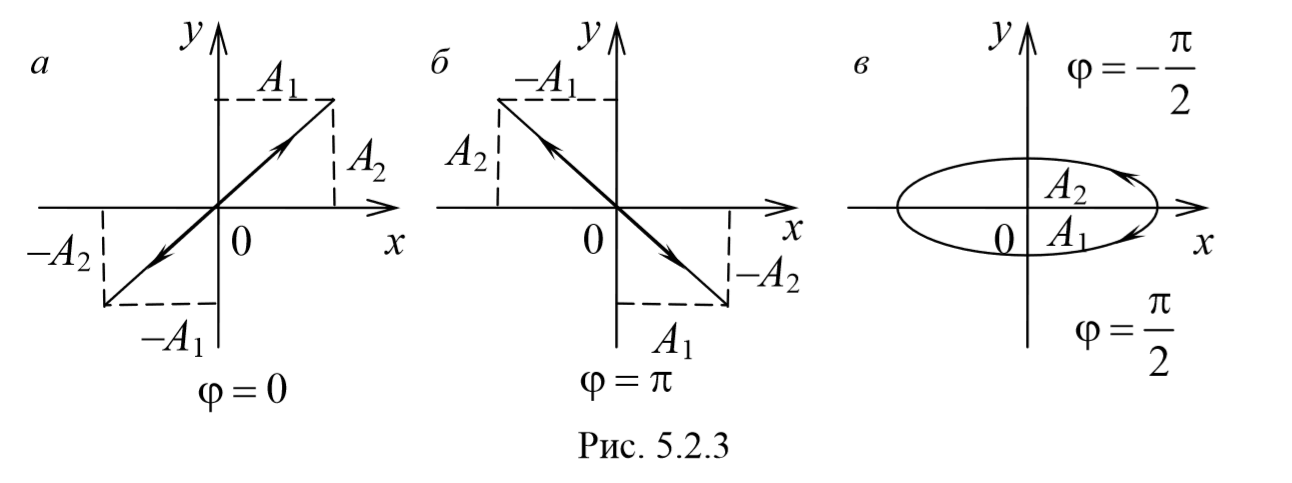
Рассмотрим несколько частных случаев и определим форму траектории для них:

a) разность фаз равна нулю [φ=0]

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

Продифференцируем по времени уравнение гармонических колебаний

и получим выражение для скорости

Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

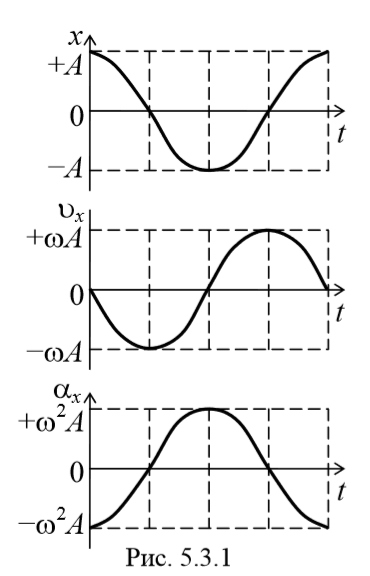
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

ω₀ − собственная частота осциллятора.

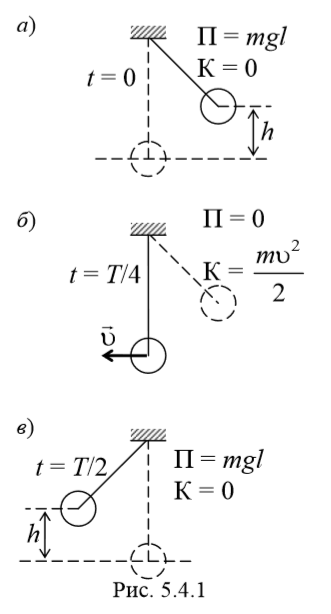
5.4. Энергия гармонических колебаний.

В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.

Потенциальная энергия тела, совершающего гармонические колебания равна

Кинетическая энергия тела, совершающего гармонические колебания равна

Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом

Следовательно, полная энергия гармонического колебания

оказывается постоянной в случае гармонических колебаний.

Найдем среднее значение потенциальной энергии за период колебания

Аналогично получается для среднего значение кинетической энергии

Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2

5.5. Пружинный, математический и физический маятники.

Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.

Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса.

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

будет иметь такой же период колебаний, что и данный физический маятник.

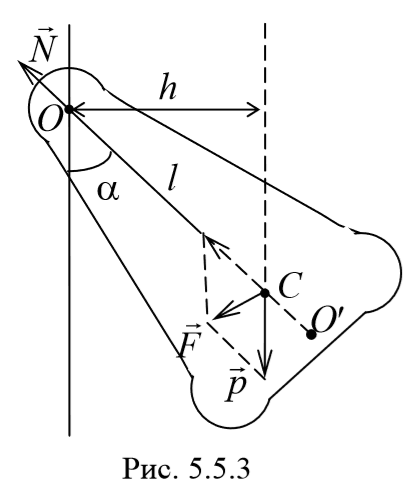
Величина l_пр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Источник

Дифференциальные уравнения колебаний

— гармонические,

— затухающие,

— вынужденные.

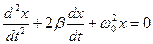
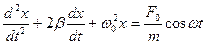
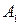
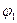
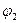
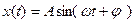
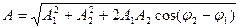
· Уравнение колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления, амплитуды колебаний которых и , а начальные фазы и ,

, где

—

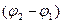
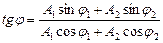
амплитуда результирующего колебания, — разность фаз слагаемых колебаний; начальная фаза результирующего колебания определяется формулой

.

· Уравнение траектории точки, участвующей в двух взаимно­ перпенди­кулярных колебаниях с одинаковыми частотами

:

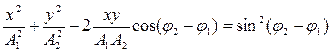
а) если 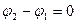, то — уравнение прямой,

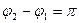
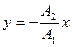
б) если , то — уравнение прямой,

в) если 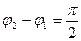, то — уравнение эллипса, приведённого к осям,

г) если и , то — уравнение окружности, где — радиус окружности.

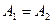
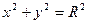
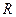
МЕХАНИЧЕСКИЕ ВОЛНЫ

· Длина волны, т.е расстояние между ближайшими частицами, колеблющимися в одинаковой фазе

,

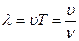
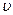
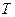
где — скорость волны, — период, — частота.

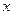
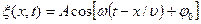
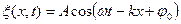
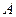
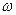
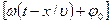
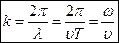
· Уравнение бегущей волны, распространяющейся вдоль положительного направления оси в среде, не поглощающей энергию,

или

, где

— амплитуда волны, — циклическая частота, -фаза волны, — начальная фаза, — волновое число.

Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны. Волна называется поперечной, если частицы колеблются в плоскостях, перпендикулярных направлению распространения волны.

Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т.е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела. Продольные волны могут распространяться как в твердых телах, так и в жидких и газообразных средах.

Маятник

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.

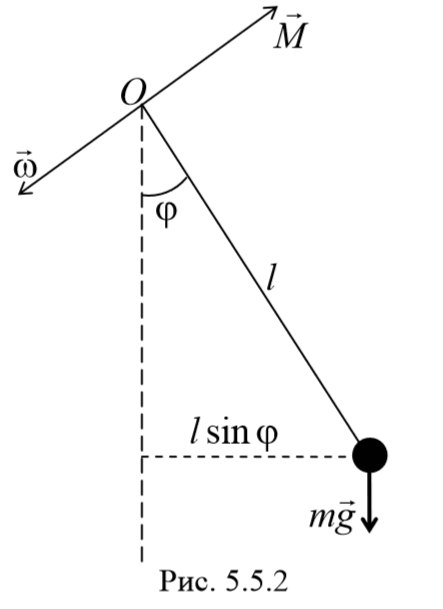
Отклонение маятника от положения равновесия будем характеризовать углом образованным нитью с вертикалью (рис. 54.1). При отклонении маятника от положения равновесия возникает вращательный момент N, равный по величине — масса, a l — длина маятника). Он имеет такое направление, что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению нужно приписывать противоположные знаки 1). Следовательно, выражение для вращательного момента имеет вид

Напишем для маятника уравнение динамики вращательного движения. Обозначив угловое ускорение через и учитывая, что момент инерции маятника равен получаем:

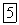
Последнее уравнение можно привести к виду

(54.2)

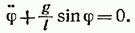
Ограничимся рассмотрением малых колебаний. В этом случае можно положить Введя, кроме того, обозначение

придем к уравнению

к зторое идентично с уравнением (53.1). Его решение имеет вид

Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону.

Как следует из (54.3), частота колебаний математического маятника зависит только от длины маятника и от ускорения силы тяжести и не зависит от массы маятника. По формуле (53.8) с учетом (54.3) получается известное из школьного курса выражение для периода колебаний математического маятника:

Отметим, что, решив уравнение (54.2), можно найти для периода колебаний следующую формулу:

где а — амплитуда колебаний, т. е. наибольший угол, на который отклоняется маятник из положения равновесия.

Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m — масса маятника, а l — расстояние между точкой подвеса О и центром масс С маятника (рис. 54.2). Знак «—» имеет то же значение, что и в случае формулы (54.1).

Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать:

В случае малых колебаний (54.8) переходит в уже известное нам уравнение:

Через обозначена в данном случае следующая величина:

(54.10)

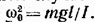
Из уравнений (54.9) и (54.10) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром масс маятника. В соответствии с (54.10) период колебаний физического маятника определяется выражением

(54.11)

Из сопоставления формул (54.6) и (54.11) получается, что математический маятник с длиной

(54.12)

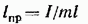
будет иметь такой период колебаний, как и данный физический маятник. Величину (54.12) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника — это длина такого математического маятника, период колебании которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см.точку О на рис. 54.2).

Можно показать (рекомендуем это сделать в порядке упражнения), что при подвешивании маятника в центре качания О приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится нозым центром качания.

На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно Измерив период колебаний маятника и зная можно по формуле

найти ускорение свободного падения .

Источник