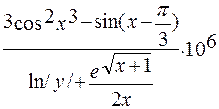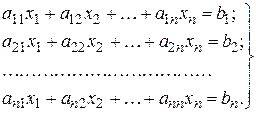Основные математические функции MatLab



MatLab содержит в себе все распространенные математические функции, которые доступны по их имени при реализации алгоритмов. Например, функция sqrt() позволяет вычислять квадрат числа и может быть использована в программе следующим образом:
Аналогичным образом вызываются и все другие математические функции, представленные в табл. 1.2.
Таблица 1.2. Основные математические функции MatLab
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
Почти все элементарные функции допускают вычисления и с комплексными аргументами. Например:
Ниже показан пример задания вектора с именем a, и содержащий значения 1, 2, 3, 4:
a = [1 2 3 4]; % вектор-строка
Для доступа к тому или иному элементу вектора используется следующая конструкция языка:
disp( a(1) ); % отображение значения 1-го элемента вектора
disp( a(2) ); % отображение значения 2-го элемента вектора
disp( a(3) ); % отображение значения 3-го элемента вектора
disp( a(4) ); % отображение значения 4-го элемента вектора
т.е. нужно указать имя вектора и в круглых скобках написать номер индекса элемента, с которым предполагается работать. Например, для изменения значения 2-го элемента массива на 10 достаточно записать
a(2) = 10; % изменение значения 2-го элемента на 10
Часто возникает необходимость определения общего числа элементов в векторе, т.е. определения его размера. Это можно сделать, воспользовавшись функцией length() следующим образом:
N = length(a); % (N=4) число элементов массива а
Если требуется задать вектор-столбец, то это можно сделать так
a = [1; 2; 3; 4]; % вектор-столбец
b = [1 2 3 4]’; % вектор-столбец
при этом доступ к элементам векторов осуществляется также как и для векторов-строк.
Следует отметить, что векторы можно составлять не только из отдельных чисел или переменных, но и из векторов. Например, следующий фрагмент программы показывает, как можно создавать один вектор на основе другого:
a = [1 2 3 4]; % начальный вектор a = [1 2 3 4]
b = [a 5 6]; % второй вектор b = [1 2 3 4 5 6]
Здесь вектор b состоит из шести элементов и создан на основе вектора а. Используя этот прием, можно осуществлять увеличение размера векторов в процессе работы программы:
a = [a 5]; % увеличение вектора а на один элемент
Недостатком описанного способа задания (инициализации) векторов является сложность определения векторов больших размеров, состоящих, например, из 100 или 1000 элементов. Чтобы решить данную задачу, в MatLab существуют функции инициализации векторов нулями, единицами или случайными значениями:
a1 = zeros(1, 100); % вектор-строка, 100 элементов с
% нулевыми значениями
a2 = zeros(100, 1); % вектор-столбец, 100 элементов с
% нулевыми значениями
a3 = ones(1, 1000); % вектор-строка, 1000 элементов с
% единичными значениями
a4 = ones(1000, 1); % вектор-столбец, 1000 элементов с
% единичными значениями
a5 = rand(1000, 1); % вектор-столбец, 1000 элементов со
% случайными значениями
Матрицы в MatLab задаются аналогично векторам с той лишь разницей, что указываются обе размерности. Приведем пример инициализации единичной матрицы размером 3х3:
E = [1 0 0; 0 1 0; 0 01]; % единичная матрица 3х3
E = [1 0 0
0 1 0
0 0 1]; % единичная матрица 3х3
Аналогичным образом можно задавать любые другие матрицы, а также использовать приведенные выше функции zeros(), ones() и rand(), например:
A1 = zeros(10,10); % нулевая матрица 10х10 элементов

A2 = zeros(10); % нулевая матрица 10х10 элементов
A3 = ones(5); % матрица 5х5, состоящая из единиц
A4 = rand(100); % матрица 100х100, из случайных чисел
Для доступа к элементам матрицы применяется такой же синтаксис как и для векторов, но с указанием строки и столбца где находится требуемый элемент:
A = [1 2 3;4 5 6;7 8 9]; % матрица 3х3
disp( A(2,1) ); % вывод на экран элемента, стоящего во
% второй строке первого столбца, т.е. 4
disp( A(1,2) ); % вывод на экран элемента, стоящего в
% первой строке второго столбца, т.е. 2
Также возможны операции выделения указанной части матрицы, например:
B1 = A(:,1); % B1 = [1; 4; 7] – выделение первого столбца
B2 = A(2,:); % B2 = [1 2 3] – выделение первой строки
B3 = A(1:2,2:3); % B3 = [2 3; 5 6] – выделение первых двух
% строк и 2-го и 3-го столбцов матрицы А.
Размерность любой матрицы или вектора в MatLab можно определить с помощью функции size(), которая возвращает число строк и столбцов переменной, указанной в качестве аргумента:
a = 5; % переменная а
A = [1 2 3]; % вектор-строка
B = [1 2 3; 4 5 6]; % матрица 2х3
size(a) % 1х1
size(A) % 1х3
size(B) % 2х3
Основные математические функции MatLab
В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.
Некоторые часто используемые математические функции:
· exp(x)–экспонента числа x;
· log(x)– натуральный логарифм;
· log10(x)– десятичный логарифм;
· sqrt(x)– квадратный корень;
· abs(x)– абсолютное значение x;
· mod(x, y)– остаток от целочисленного деления с учетом знака;
· rem(x, y)– остаток от целочисленного деления без учета знака;
· real(z)– вещественная часть комплексного числа;
· imag(z)– мнимая часть комплексного числа;
· round(x)– округление до ближайшего целого.
Более полный список основных математических функций MatLab:
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x,y) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:
Вычислить: res=
Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.
Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные. Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.
res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – m.
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить нужный каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Дата добавления: 2016-04-02 ; просмотров: 5522 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Matlab модуль числа
Основные математические функции MatLab
В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.
Некоторые часто используемые математические функции:
· exp(x)–экспонента числа x;
· log(x)– натуральный логарифм;
· log10(x)– десятичный логарифм;
· sqrt(x)– квадратный корень;
· abs(x)– абсолютное значение x;
· mod(x, y)– остаток от целочисленного деления с учетом знака;
· rem(x, y)– остаток от целочисленного деления без учета знака;
· real(z)– вещественная часть комплексного числа;
· imag(z)– мнимая часть комплексного числа;
· round(x)– округление до ближайшего целого.
Более полный список основных математических функций MatLab:
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x,y) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:
Вычислить: res=
Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.
Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные. Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.
res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – m.
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить нужный каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Дата добавления: 2016-04-02 ; просмотров: 1590 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Основные математические функции MatLab
MatLab содержит в себе все распространенные математические функции, которые доступны по их имени при реализации алгоритмов. Например, функция sqrt() позволяет вычислять квадрат числа и может быть использована в программе следующим образом:
x = 2;
y = 4;
d = sqrt(x^2+y^2); %вычисление евклидового расстояния
Аналогичным образом вызываются и все другие математические функции, представленные в табл. 1.2.
Таблица 1.2. Основные математические функции MatLab
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
Почти все элементарные функции допускают вычисления и с комплексными аргументами. Например:
Ниже показан пример задания вектора с именем a, и содержащий значения 1, 2, 3, 4:
a = [1 2 3 4]; % вектор-строка
Для доступа к тому или иному элементу вектора используется следующая конструкция языка:
disp( a(1) ); % отображение значения 1-го элемента вектора
disp( a(2) ); % отображение значения 2-го элемента вектора
disp( a(3) ); % отображение значения 3-го элемента вектора
disp( a(4) ); % отображение значения 4-го элемента вектора
т.е. нужно указать имя вектора и в круглых скобках написать номер индекса элемента, с которым предполагается работать. Например, для изменения значения 2-го элемента массива на 10 достаточно записать
a(2) = 10; % изменение значения 2-го элемента на 10
Часто возникает необходимость определения общего числа элементов в векторе, т.е. определения его размера. Это можно сделать, воспользовавшись функцией length() следующим образом:
N = length(a); % (N=4) число элементов массива а
Если требуется задать вектор-столбец, то это можно сделать так
a = [1; 2; 3; 4]; % вектор-столбец
b = [1 2 3 4]’; % вектор-столбец
при этом доступ к элементам векторов осуществляется также как и для векторов-строк.
Следует отметить, что векторы можно составлять не только из отдельных чисел или переменных, но и из векторов. Например, следующий фрагмент программы показывает, как можно создавать один вектор на основе другого:
a = [1 2 3 4]; % начальный вектор a = [1 2 3 4]
b = [a 5 6]; % второй вектор b = [1 2 3 4 5 6]
Здесь вектор b состоит из шести элементов и создан на основе вектора а. Используя этот прием, можно осуществлять увеличение размера векторов в процессе работы программы:
a = [a 5]; % увеличение вектора а на один элемент
Недостатком описанного способа задания (инициализации) векторов является сложность определения векторов больших размеров, состоящих, например, из 100 или 1000 элементов. Чтобы решить данную задачу, в MatLab существуют функции инициализации векторов нулями, единицами или случайными значениями:
a1 = zeros(1, 100); % вектор-строка, 100 элементов с
% нулевыми значениями
a2 = zeros(100, 1); % вектор-столбец, 100 элементов с
% нулевыми значениями
a3 = ones(1, 1000); % вектор-строка, 1000 элементов с
% единичными значениями
a4 = ones(1000, 1); % вектор-столбец, 1000 элементов с
% единичными значениями
a5 = rand(1000, 1); % вектор-столбец, 1000 элементов со
% случайными значениями
Матрицы в MatLab задаются аналогично векторам с той лишь разницей, что указываются обе размерности. Приведем пример инициализации единичной матрицы размером 3х3:
E = [1 0 0; 0 1 0; 0 01]; % единичная матрица 3х3
E = [1 0 0
0 1 0
0 0 1]; % единичная матрица 3х3
Аналогичным образом можно задавать любые другие матрицы, а также использовать приведенные выше функции zeros(), ones() и rand(), например:
A1 = zeros(10,10); % нулевая матрица 10х10 элементов
A2 = zeros(10); % нулевая матрица 10х10 элементов
A3 = ones(5); % матрица 5х5, состоящая из единиц
A4 = rand(100); % матрица 100х100, из случайных чисел
Для доступа к элементам матрицы применяется такой же синтаксис как и для векторов, но с указанием строки и столбца где находится требуемый элемент:
A = [1 2 3;4 5 6;7 8 9]; % матрица 3х3
disp( A(2,1) ); % вывод на экран элемента, стоящего во
% второй строке первого столбца, т.е. 4
disp( A(1,2) ); % вывод на экран элемента, стоящего в
% первой строке второго столбца, т.е. 2
Также возможны операции выделения указанной части матрицы, например:
B1 = A(:,1); % B1 = [1; 4; 7] – выделение первого столбца
B2 = A(2,:); % B2 = [1 2 3] – выделение первой строки
B3 = A(1:2,2:3); % B3 = [2 3; 5 6] – выделение первых двух
% строк и 2-го и 3-го столбцов матрицы А.
Размерность любой матрицы или вектора в MatLab можно определить с помощью функции size(), которая возвращает число строк и столбцов переменной, указанной в качестве аргумента:
a = 5; % переменная а
A = [1 2 3]; % вектор-строка
B = [1 2 3; 4 5 6]; % матрица 2х3
size(a) % 1х1
size(A) % 1х3
size(B) % 2х3
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8826 — 

Стандартные функции Matlab
Все операции в Matlab ориентированы прежде всего на работу с матрицами, но могут выть использованы при работе с векторами и скалярными переменными.
Элементарные функции Matlab. К ним относятся следующие функции:
sin(x) sinh(x) asin(x) asinh(x)
cos(x) cosh(x) acos(x) acosh(x)
tan(x) tanh(x) atan(x) atan2(x,y) atanh(x)
cot(x) coth(x) acot(x) acoth(x)
exp(x) log(x) log10(x) log2(x) pow2(x) sqrt(x)
Функции комплексного аргумента:
abs(z) – модуль комплексного числа; angle(z) – аргумент;
complex(x, y) – формирование комплексного числа x+y*i;
conj(z) – возвращает комплексно-сопряженное (по отношению к z) число;
real(z) – возвращает действительную часть; imag(z) – мнимую часть.
Функции округления и нецелочисленного деления:
fix(x) – округление в сторону к нулю, floor(x) – к –¥, ceil(x) – к +¥,
round(x) – до ближайшего целого;
mod(x, y) – остаток от деления x/y с учетом знака,
rem(x, y) – то же, без учета знака;
sign(x) – знак числа (+1/–1).
Элементарные функции, как и всякие другие, имеют один результат (массив). Элементарные функции могут быть использованы с одинаковым синтаксисом как для чисел, так и для массивов.
Пример 1. Разный тип параметров
Различают матричные и поэлементные арифметические операции.
+ – уточнение знака (унарная), сложение;
– – изменение знака (унарная), вычитание;
Поскольку математический смысл операций матричного и поэлементного сложения и вычитания идентичен:
C = A ± B означает
синтаксис матричных и поэлементных операций сложения и вычитания одинаков, в них используются одни и те же символы операций.
* – скалярное матричное умножение;
^ – матричное возведение в степень;
.^ – поэлементное возведение в степень;
– матричное деление слева;
/ – матричное деление справа;
.’ – несопряженное транспонирование (унарная).
Все арифметические операции, за исключением указанных, являются бинарными.
» A=[1 2 3; 4 5 6]; B=[7 8 9; 3 2 1];
Для операции * (матричное произведение) матрица-сомножитель2 должна иметь столько строк, сколько столбцов имеет матрица-сомножитель1:
 |
Inner matrix dimensions must agree.
» Ac=[1+2i 1+3i 1+4i; 2+3i 2+4i 2+5i];
1.0000 — 2.0000i 2.0000 — 3.0000i
1.0000 — 3.0000i 2.0000 — 4.0000i
1.0000 — 4.0000i 2.0000 — 5.0000i
1.0000 + 2.0000i 2.0000 + 3.0000i
1.0000 + 3.0000i 2.0000 + 4.0000i
1.0000 + 4.0000i 2.0000 + 5.0000i
Операция ^ (матричное возведение в степень) выполняется только для квадратных матриц, и означает умножение матрицы саму на себя заданное число раз (второй операнд обязательно скаляр):
-0.9100 — 3.5442i 0.4163 + 1.6212i
Последняя операция широко используется при решении систем линейных уравнений вида
Действительно, представив систему уравнений в матричной форме:
откуда решение системы уравнений:
Пример. Решить систему уравнений
Решение сводится к набору в интерактивном режиме следующих команд:
Проверку вычисления корней можно выполнить следующим образом:
| – логическое «или» (0|0 – 0, 1|0 – 1, 0|1 – 1, 1|1 – 1);
xor – логическое исключающее «или» (0xor0 – 0, 0xor1 – 1, 1xor0 – 1, 1xor1 – 0);
Если логические операции (а также логические функции) выполняются над действительными числами, то ложью считают число нуль, а истиной – все числа, не равные нулю.
Операции отношения (сравнения)
> – больше; >= – больше или равно; 1
» A=[1 8 3; 6 2 5]; B=[4 3 1; 2 6 8];
1.0000 2.0000 3.0000 4.0000
zeros – матрица, состоящая из нулей; ones – матрица, состоящая из единиц;
rand – матрица, состоящая из случ. чисел с равномерным распределением;
randn – матрица, состоящая из случ. Чисел с нормальным распределением.
zeros(n) – формирует квадратную матрицу n´n, состоящую из нулей;
zeros(m, n) – формирует матрицу m´n, состоящую из нулей;
(zeros(1, n) – вектор-строка; zeros(m, 1) – вектор-столбец)
zeros(size(A)) – формирует матрицу, состоящую из нулей, той же размерности, что и матрица A.
Формат обращения к функциям ones, rand и randn аналогичный.
Разницу между функциями rand и randn можно показать графически:
» xr=rand(1,100); xrs=sort(xr); bar(xrs)
» yr=randn(1,100); yrs=sort(yr); bar(yrs)
eye(n) – формирует единичную диагональную матрицу n´n.
diag(B) (B – двухмерная матрица) – выделяет главную диагональ матрицы B и помещает ее в вектор-столбец;
diag(x) (x – вектор) – формирует диагональную матрицу, используя вектор x в качестве главной диагонали.
» A=[1 2 3; 4 5 6; 7 8 9];
Манипуляции с матрицами
tril (A) – формирует треугольную матрицу как нижнюю часть от матрицы A;
triu(A) – формирует треугольную матрицу как верхнюю часть от матрицы А.
» A=[1 2 3; 4 5 6; 7 8 9];
lu(A) – разложение Холецкого – заменяет квадратную матрицу A скалярным произведением двух треугольных матриц L и U методом Гаусса:
» A=[1 2 3; 4 5 6; 7 8 9];
det(A) – возвращает определитель квадратной матрицы A.
fliplr(A) – поворот матрицы A на 180° в горизонтальном направлении;
flipud(A) – поворот матрицы A на 180° в вертикальном направлении;
rot90(A) – поворот матрицы A на 90° против часовой стрелки;
rot90(A, k) – поворот матрицы A на k*90° против часовой стрелки (k – целое число).
Манипуляции с векторами
cross(x, y) – векторное произведение векторов x и y в трехмерном пространстве;
cross(A, B, dim) – векторное произведение многомерных массивов A и B по размерности dim;
dot(x, y) – скалярное произведение векторов x и y;
dot(A, B, dim) – скал. произведение многомерных массивов A и B по размерности dim.
Длины векторов x и y, а также длина матриц A и B по размерности dim должны быть равны 3.
Базовые операции анализа
Пусть a,b,c – числа, х,у,z – векторы, А,В,C – матрицы.
c=max(a, b) – возвращает максимальное из двух чисел a и b (при комплексных аргументах по умолчанию сравниваются модули):
z=max(x, y) – вектор той же размерности, что x и y, составленный из максимальных элементов векторов;
xmax=max(x) – максимальный элемент вектора x;
[xmax, imax]=max(x) – дополнительно записывает адрес максимального элемента в числовую переменную imax (если максимальных элементов несколько, возвращается адрес первого из них);
amax=max(A) – возвращает вектор-строку amax из максимальных элементов столбцов матрицы А;
[amax, imax]=max(A) – дополнительно формируется вектор-строка imax, составленный из номеров строк, в которых расположены максимальные элементы столбцов.
» a=1; b=2; x=[1 3 2]; y=[2 1 3]; A=[1 2 3; 4 5 6]; B=[3 2 1; 6 5 4];
Символьные вычисления в Matlab
Здравствуйте, уважаемые читатели. В этой небольшой статье речь пойдет о работе с символьными переменными в Matlab. На простых примерах мы разберем преобразование символьных выражений, а также символьное дифференцирование и интегрирование.
Создание символьного выражения в Matlab
Иногда символьные выражения крайне необходимы, именно поэтому важно уметь их объявлять в Matlab. Обычно используют два способа. Первый — использование оператора syms.
Таким простым способом мы создали две символьные переменные. Пока они ничего не делают и не представляют какой либо ценности, но чуть позже мы увидим, что они могут быть полезны.
Второй способ — использование команды sym.
При ее использовании, можно сразу задать функцию, полином или выражение:
Символьные выражения полезны тем, что вычисления с ними производятся без погрешностей.
Преобразования символьных выражений в Matlab
Возможны несколько типов преобразований:
Для примера зададим символьное выражение и попробуем раскрыть скобки:
Данная функция помогает упростить символьное выражение в Matlab. Возьмем для примера такое выражение.
Данная функция помогает преобразовать символьное выражение, например, в полином в Matlab. Иногда, это бывает очень важно и необходимо.
Вычисление значения символьных выражений в Matlab
Конечно, символьные выражения это интересный инструмент в Matlab, но хотелось бы находить значение этого выражения при каких-то заданных значениях переменной.
Для этого можно воспользоваться несколькими функциями. Сначала нужно заменить все переменные на число с помощью оператора subs. Затем перевести полученное выражение в числовое с помощью оператора double. Разберем пример:
Стоит отметить, что после выполнения оператора subs, выражение все еще остается символьным. Поэтому далее выполняется оператор double.
Если же у функции несколько переменных, то придется использовать subs несколько раз.
Символьное дифференцирование в Matlab
На нашем сайте уже были статьи по численному дифференцированию в среде Matlab, но любой численный метод может давать погрешности. А вычисление в символьном виде может быть очень полезным и точным.
Итак, символьное дифференцирование осуществляется оператором diff. При вызове функции следует указать переменную, по которой будет производиться дифференцирование.
В этом примере функция зависит от одной переменной, поэтому производная считается по ней автоматически. Если нужно вычислить вторую производную:
Теперь посмотрим на функцию от нескольких переменных:
Очевидно, что после получения производных, с ними можно выполнить все действия, описанные выше.
Символьное интегрирование в Matlab
Наряду с дифференцированием, в Matlab можно выполнять символьное интегрирование. Иногда это бывает удобнее, чем численное интегрирование. Символьное интегрирование в Matlab выполняется оператором int.
Оператор выполняется практически также, как и оператор дифференцирования.
Также, возможен расчет определенного интеграла:
Другие функции
В Matlab реализовано множество функций для работы с символьными вычислениями. Помимо тех, что были рассмотрены, следует выделить следующие функции:
Эти и многие другие функции в Matlab имеют свои опции и параметры. Очевидно, что среда Matlab дает широкие возможности разработчику при работе с символьными вычислениями.
Заключение
На этом статья подходит к концу. Символьные вычисления в Matlab являются дополнительным инструментом разработчика, и с помощью этой статьи можно ознакомиться с этим инструментом.
Все примеры очень просты и в исходниках не нуждаются. На этом все, встретимся в следующей статье.