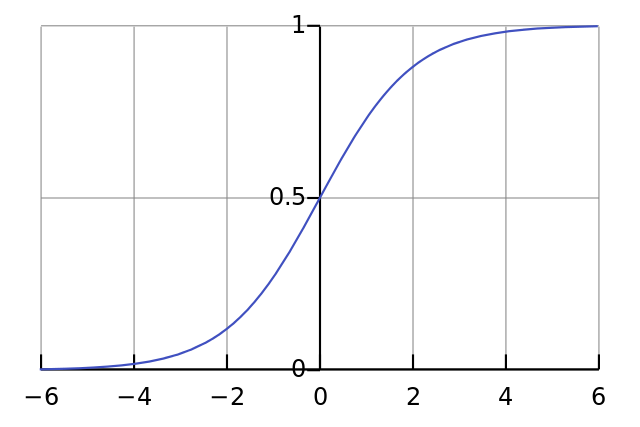
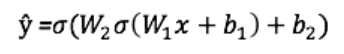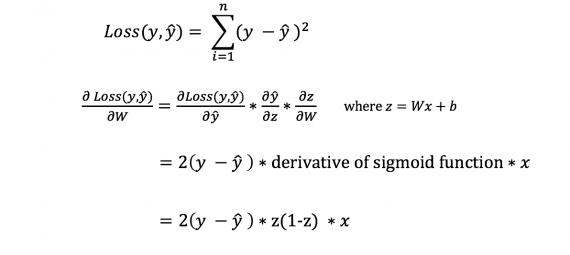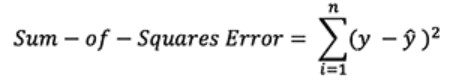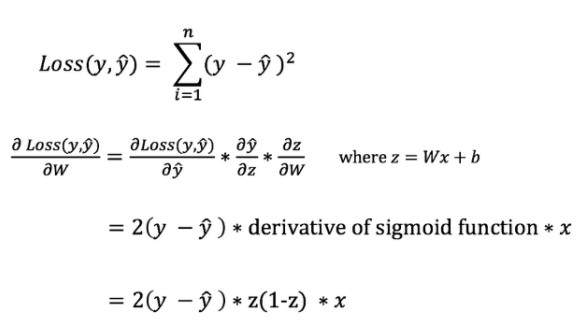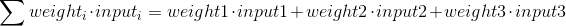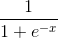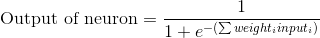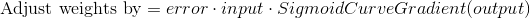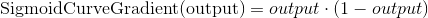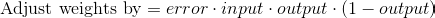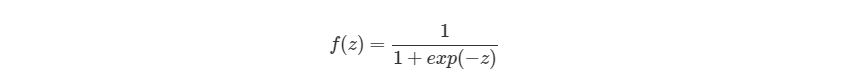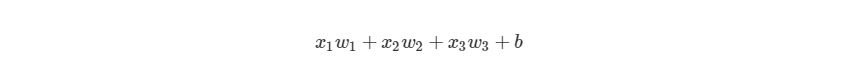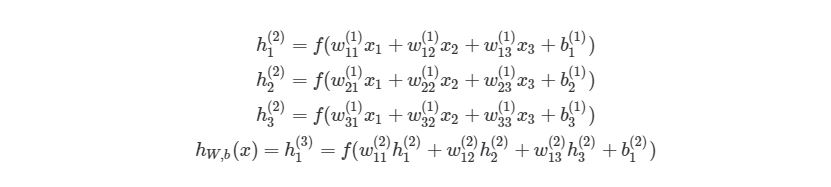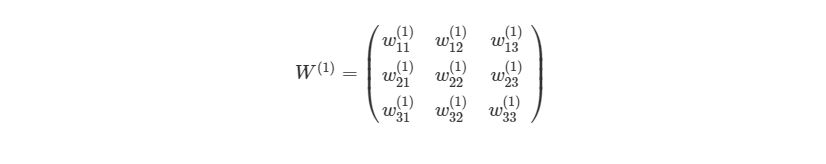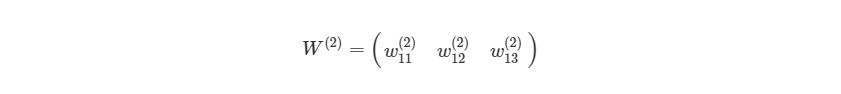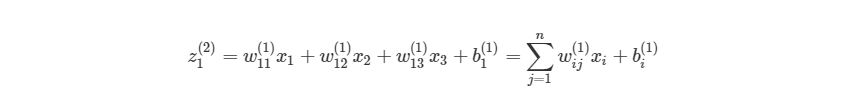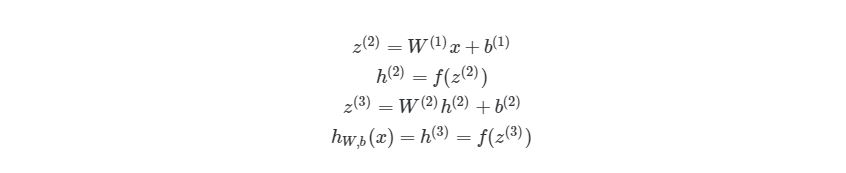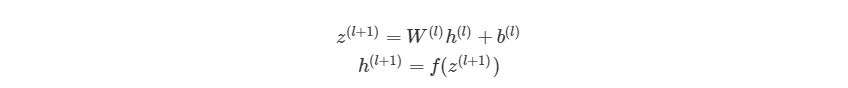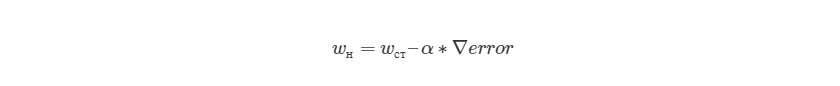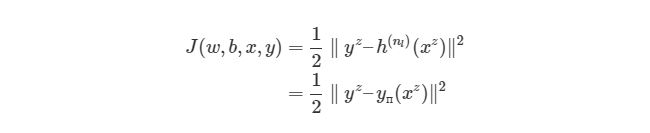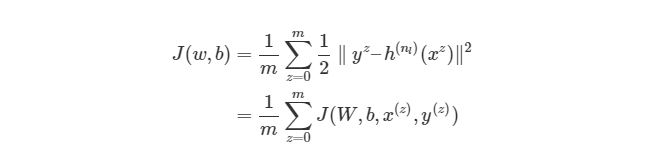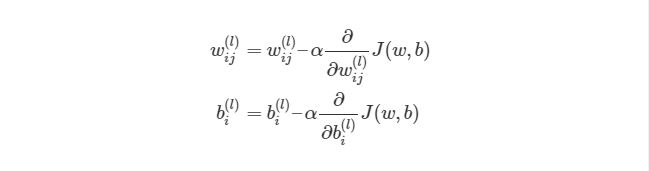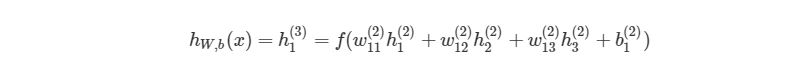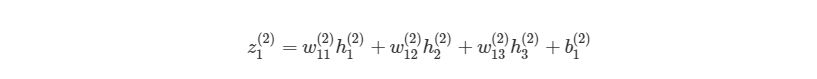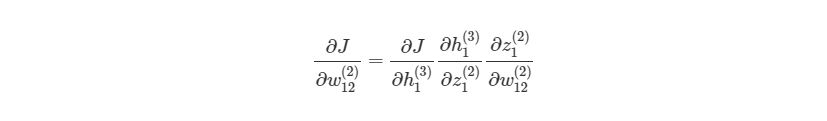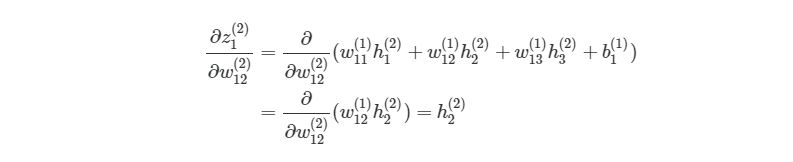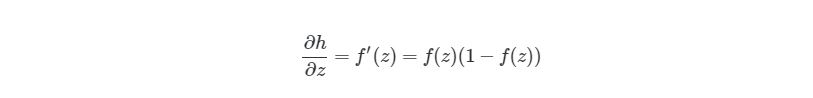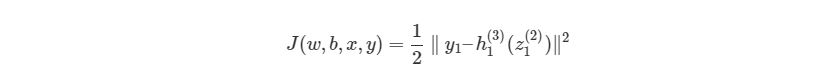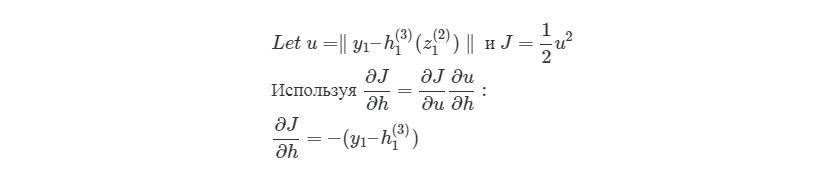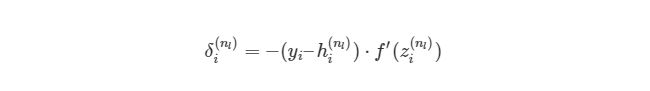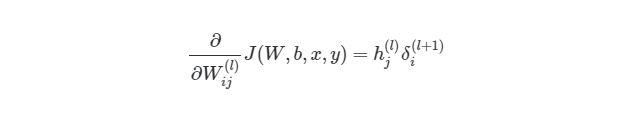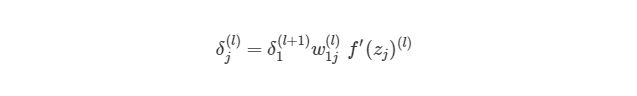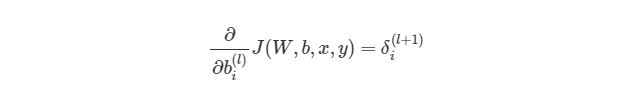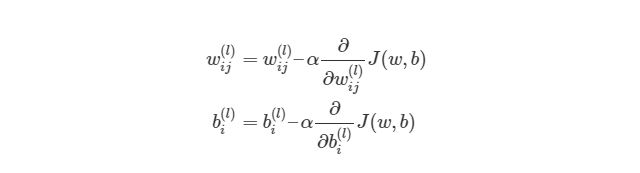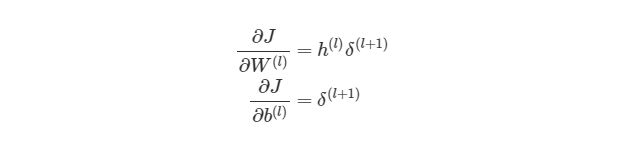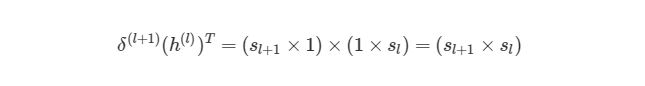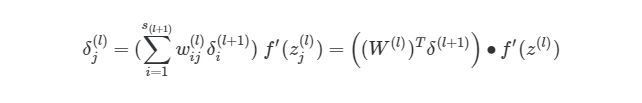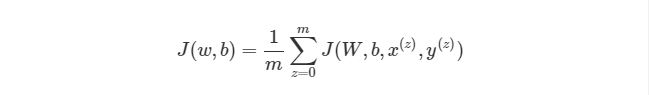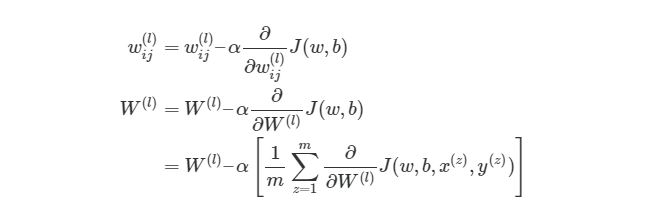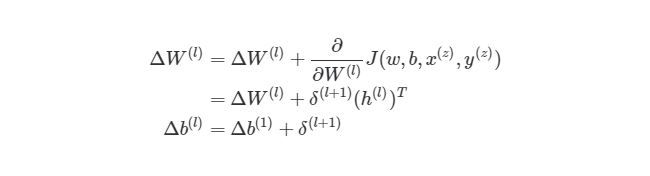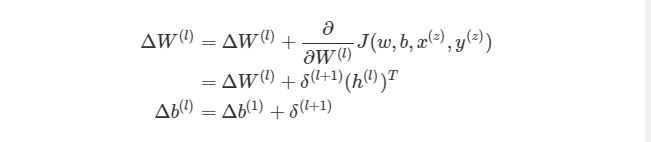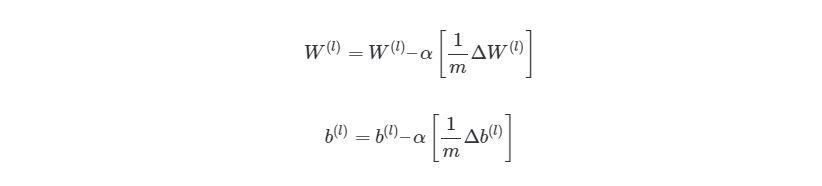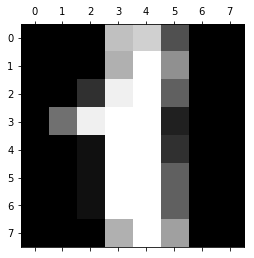Как создать собственную нейронную сеть с нуля на языке Python
Джеймс Лой, Технологический университет штата Джорджия. Руководство для новичков, после которого вы сможете создать собственную нейронную сеть на Python.
Мотивация: ориентируясь на личный опыт в изучении глубокого обучения, я решил создать нейронную сеть с нуля без сложной учебной библиотеки, такой как, например, TensorFlow. Я считаю, что для начинающего Data Scientist-а важно понимание внутренней структуры нейронной сети.
Эта статья содержит то, что я усвоил, и, надеюсь, она будет полезна и для вас! Другие полезные статьи по теме:
Что такое нейронная сеть?
Большинство статей по нейронным сетям при их описании проводят параллели с мозгом. Мне проще описать нейронные сети как математическую функцию, которая отображает заданный вход в желаемый результат, не вникая в подробности.
Нейронные сети состоят из следующих компонентов:
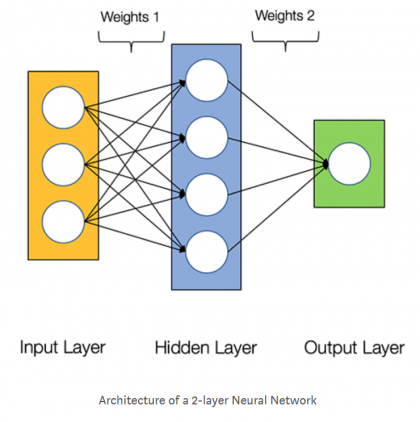
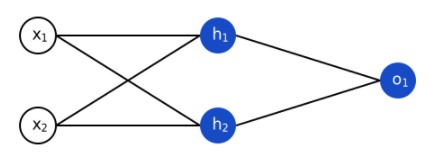
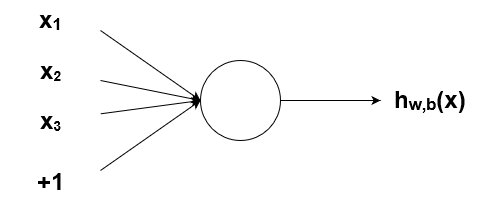
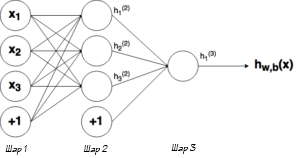
На приведенной ниже диаграмме показана архитектура двухслойной нейронной сети (обратите внимание, что входной уровень обычно исключается при подсчете количества слоев в нейронной сети).
Создание класса Neural Network на Python выглядит просто:
Обучение нейронной сети
Выход ŷ простой двухслойной нейронной сети:
В приведенном выше уравнении, веса W и смещения b являются единственными переменными, которые влияют на выход ŷ.
Естественно, правильные значения для весов и смещений определяют точность предсказаний. Процесс тонкой настройки весов и смещений из входных данных известен как обучение нейронной сети.
Каждая итерация обучающего процесса состоит из следующих шагов
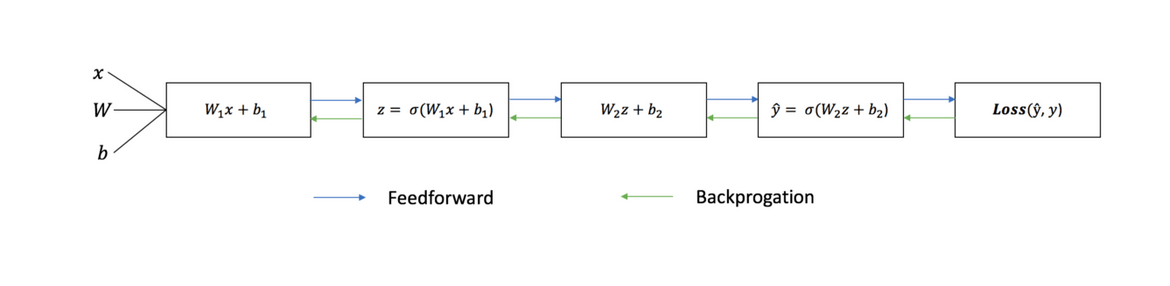
Последовательный график ниже иллюстрирует процесс:
Прямое распространение
Как мы видели на графике выше, прямое распространение — это просто несложное вычисление, а для базовой 2-слойной нейронной сети вывод нейронной сети дается формулой:
Давайте добавим функцию прямого распространения в наш код на Python-е, чтобы сделать это. Заметим, что для простоты, мы предположили, что смещения равны 0.
Однако нужен способ оценить «добротность» наших прогнозов, то есть насколько далеки наши прогнозы). Функция потери как раз позволяет нам сделать это.
Функция потери
Есть много доступных функций потерь, и характер нашей проблемы должен диктовать нам выбор функции потери. В этой работе мы будем использовать сумму квадратов ошибок в качестве функции потери.
Сумма квадратов ошибок — это среднее значение разницы между каждым прогнозируемым и фактическим значением.
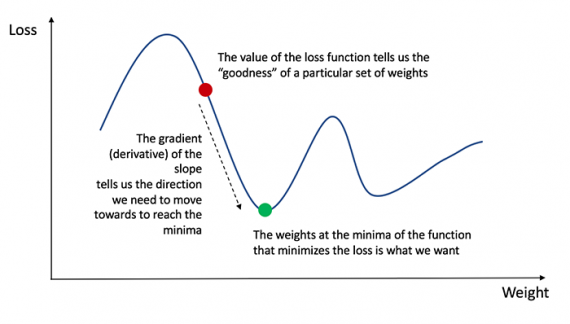
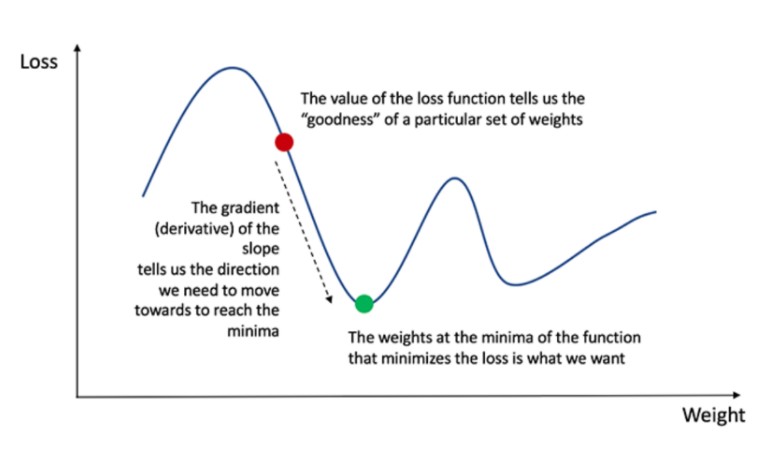
Цель обучения — найти набор весов и смещений, который минимизирует функцию потери.
Обратное распространение
Теперь, когда мы измерили ошибку нашего прогноза (потери), нам нужно найти способ распространения ошибки обратно и обновить наши веса и смещения.
Чтобы узнать подходящую сумму для корректировки весов и смещений, нам нужно знать производную функции потери по отношению к весам и смещениям.
Напомним из анализа, что производная функции — это тангенс угла наклона функции.
Если у нас есть производная, то мы можем просто обновить веса и смещения, увеличив/уменьшив их (см. диаграмму выше). Это называется градиентным спуском.
Однако мы не можем непосредственно вычислить производную функции потерь по отношению к весам и смещениям, так как уравнение функции потерь не содержит весов и смещений. Поэтому нам нужно правило цепи для помощи в вычислении.
Фух! Это было громоздко, но позволило получить то, что нам нужно — производную (наклон) функции потерь по отношению к весам. Теперь мы можем соответствующим образом регулировать веса.
Добавим функцию backpropagation (обратного распространения) в наш код на Python-е:
Проверка работы нейросети
Теперь, когда у нас есть наш полный код на Python-е для выполнения прямого и обратного распространения, давайте рассмотрим нашу нейронную сеть на примере и посмотрим, как это работает.
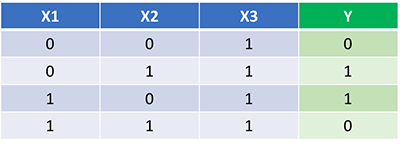
Наша нейронная сеть должна изучить идеальный набор весов для представления этой функции.
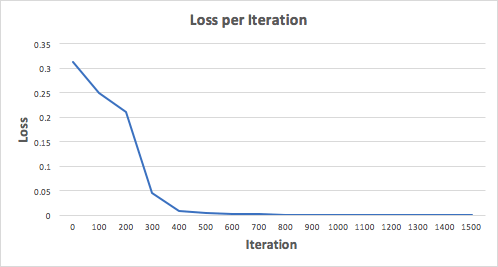
Давайте тренируем нейронную сеть на 1500 итераций и посмотрим, что произойдет. Рассматривая график потерь на итерации ниже, мы можем ясно видеть, что потеря монотонно уменьшается до минимума. Это согласуется с алгоритмом спуска градиента, о котором мы говорили ранее.
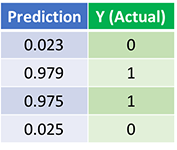
Посмотрим на окончательное предсказание (вывод) из нейронной сети после 1500 итераций.
Мы сделали это! Наш алгоритм прямого и обратного распространения показал успешную работу нейронной сети, а предсказания сходятся на истинных значениях.
Заметим, что есть небольшая разница между предсказаниями и фактическими значениями. Это желательно, поскольку предотвращает переобучение и позволяет нейронной сети лучше обобщать невидимые данные.
Финальные размышления
Я многому научился в процессе написания с нуля своей собственной нейронной сети. Хотя библиотеки глубинного обучения, такие как TensorFlow и Keras, допускают создание глубоких сетей без полного понимания внутренней работы нейронной сети, я нахожу, что начинающим Data Scientist-ам полезно получить более глубокое их понимание.
Я инвестировал много своего личного времени в данную работу, и я надеюсь, что она будет полезной для вас!
Создание простой нейронной сети на Python
Feb 26 · 8 min read
В течение последних десятилетий машинное обучение оказало огромное влияние на весь мир, и его популярность только набирает обороты. Все больше людей увлекается подотраслями этой науки, например нейронными сетями, которые разрабатываются по принципам функционирования человеческого мозга. В этой статье мы разберем код Python для простой нейронной сети, классифицирующей векторы 1х3, где первым элементом является 10.
Шаг 1: импорт NumPy, Scikit-learn и Matplotlib
Для этого проекта мы используем три пакета. NumPy будет служить для создания векторов и матриц, а также математических операций. Scikit-learn возьмет на себя обязанность по масштабированию данных, а Matpotlib предоставит график изменения показателей ошибки в процессе обучения сети.
Шаг 2: создание обучающей и контрольной выборок
Нейронны е сети отлично справляются с изучением тенденций как в больших, так и в малых датасетах. Тем не менее специалисты по данным должны иметь в виду опасность возможного переобучения, которое чаще встречается в проектах с небольшими наборами данных. Переобучение происходит, когда алгоритм слишком долго обучается на датасете, в результате чего модель просто запоминает представленные данные, давая хорошие результаты конкретно на используемой обучающей выборке. При этом она существенно хуже обобщается на новые данные, а ведь именно это нам от нее и нужно.
Чтобы гарантировать оценку модели с позиции ее возможности прогнозировать именно новые точки данных, принято разделять датасеты на обучающую и контрольную выборки (а иногда еще и на тестовую).
Шаг 3: масштабирование данных
Многие модели МО не способны понимать различия между, например единицами измерения, и будут, естественно, придавать большие веса признакам с большими величинами. Это может нарушить способность алгоритма правильно прогнозировать новые точки данных. Более того, обучение моделей МО на признаках с высокими величинами будет медленнее, чем нужно, по крайней мере при использовании градиентного спуска. Причина в том, что градиентный спуск сходится к искомой точке быстрее, когда значения находятся приблизительно в одном диапазоне.
Шаг 4: Создание класса нейронной сети
Один из простейших способов познакомиться со всеми элементами нейронной сети — создать соответствующий класс. Он должен включать все переменные и функции, которые потребуются для должной работы нейронной сети.
Шаг 4.1: создание функции инициализации
Функция _init_ вызывается при создании класса, что позволяет правильно инициализировать его переменные.
Нейронные сети на Python: как написать и обучить


Нейронные сети — это огромное множество алгоритмов в области машинного обучения. Из чего они состоят и как работают? Давайте попробуем в этом разобраться.
Нейронная сеть — это функциональная единица машинного или глубокого обучения. Она имитирует поведение человеческого мозга, поскольку основана на концепции биологических нейронных сетей.
Нейронные сети способны решать множество задач. В основном они состоят из таких компонентов:
Чтобы реализовать нейросеть, необходимо понимать, как ведут себя нейроны. Нейрон одновременно принимает несколько входов, обрабатывает эти данные и выдает один выход.
Схематическое изображение нейронной сети
Проще говоря, нейронная сеть представляет собой блоки ввода и вывода, где каждое соединение имеет соответствующие веса (это сила связи нейронов; чем вес больше, тем один нейрон сильнее влияет на другой). Данные всех входов умножаются на веса:
Входы после взвешивания суммируются с прибавлением значения порога «c»:
Полученное значение пропускается через функцию активации (сигмоиду), которая преобразует входы в один выход:
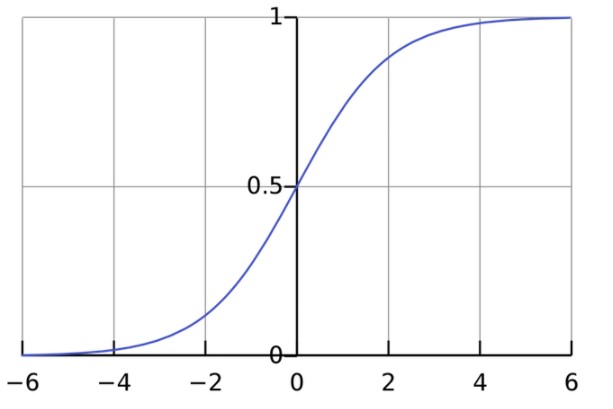
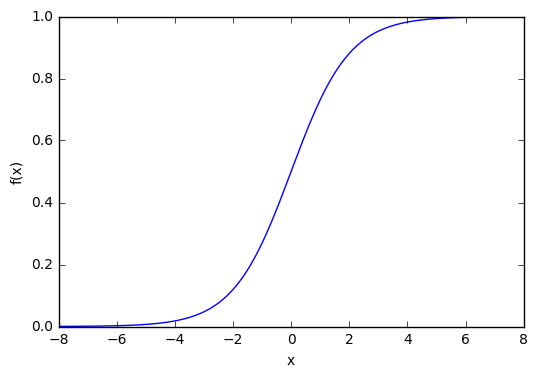
Так выглядит сигмоида:
Интервал результатов сигмоиды — от 0 до 1. Отрицательные числа стремятся к нулю, а положительные — к единице.
Пусть нейрон имеет следующие значения: w = [0,1] c = 4
Входной слой: x = 2, y = 3.
((x*w 1 ) + (y*w 2 )) + c = 2*0 + 3*1 + 4 = 7
Как написать свой нейрон
Мы использовали значения из примера выше и видим, что результаты вычислений совпадают и равны 0.99.
Как собрать нейросеть из нейронов
Нейросеть состоит из множества соединенных между собой нейронов.
Пример несложной нейронной сети:
Простая нейронная сеть
Внимание! Слоев в нейросети, так же как и нейронов, может быть любое количество.
Представим, что нейроны из графика выше имеют веса [0, 1]. Пороговое значение (b) у обоих нейронов равно 0 и они имеют идентичную сигмоиду.
При входных данных x=[2, 3] получим:
h 1 = h 2 = ƒ(w*x+b) = ƒ((0*2) + (1*3) +0) = ƒ(3) = 0.95
Входные данные по нейронам передаются до тех пор, пока не получатся выходные значения.
Код нейросети
Видим, что нейронная сеть создана, выходное значение равно 0.72.
Обучение нейронной сети
Обучение нейросети — это подбор весов, которые соответствуют всем входам для решения поставленных задач.
Класс нейронной сети:
Каждый этап процесса обучения состоит из:
Дана двуслойная нейросеть:
ŷ = σ(w 2 σ(w 1 x + b 1 ) + b 2 )
В данном случае на выход ŷ влияют только две переменные — w (веса) и b (смещение).
Настройку весов и смещений из данных входа или процесс обучения нейросети можно изобразить так:
Процесс обучения нейросети
Прямое распространение
Как видно, формула прямого распространения представляет собой несложное вычисление:
ŷ = σ(w 2 σ(w 1 x + b 1 ) + b 2 )
Далее необходимо добавить в код функцию прямого распространения. Предположим, что смещения в этом случае будут равны 0.
Чтобы вычислить ошибку прогноза, необходимо использовать функцию потери. В примере уместно воспользоваться формулой суммы квадратов ошибок — средним значением между прогнозируемым и фактическим результатами:
Формула суммы квадратов ошибок
Обратное распространение
Обратное распространение позволяет измерить производные в обратном порядке — от конца к началу, и скорректировать веса и смещения. Для этого необходимо узнать производную функции потери — тангенс угла наклона.
Тангенс угла наклона — производная функции потери
Производная функции по отношению к весам и смещениям позволяет узнать градиентный спуск.
Производная функции потери не содержит весов и смещений, для ее вычисления необходимо добавить правило цепи:
Благодаря этому правилу можно регулировать веса.
Добавляем в код Python функцию обратного распространения:
Нейронные сети базируются на определенных алгоритмах и математических функциях. Сначала может казаться, что разобраться в них довольно сложно. Но существуют готовые библиотеки машинного обучения для построения и тренировки нейросетей, позволяющие не углубляться в их устройство.
Простая нейронная сеть в 9 строк кода на Python
Из статьи вы узнаете, как написать свою простую нейросеть на python с нуля, не используя никаких библиотек для нейросетей. Если у вас еще нет своей нейронной сети, вот всего лишь 9 строчек кода:
Перед вами перевод поста How to build a simple neural network in 9 lines of Python code, автор — Мило Спенсер-Харпер. Ссылка на оригинал — в подвале статьи.
В статье мы разберем, как это получилось, и вы сможете создать свою собственную нейронную сеть на python. Также будут показаны более длинные и красивые версии кода.

Но для начала, что же такое нейронная сеть? Человеческий мозг состоит из 100 миллиарда клеток, называемых нейронами, соединенных синапсами. Если достаточное количество синаптичеких входов возбуждены, то и нейрон тоже становится возбужденным. Этот процесс также называется “мышление”.
Мы можем смоделировать этот процесс, создав нейронную сеть на компьютере. Не обязательно моделировать всю сложную модель человеческого мозга на молекулярном уровне, достаточно только высших правил мышления. Мы используем математические техники называемые матрицами, то есть просто сетки с числами. Чтобы сделать все максимально просто, построим модель из трех входных сигналов и одного выходного.
Мы будем тренировать нейрон на решение задачи, представленной ниже.
Первые четыре примера назовем тренировочной выборкой. Вы сможете выделить закономерность? Что должно стоять на месте “?”
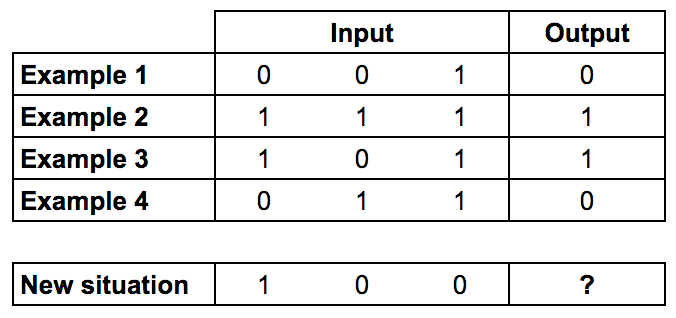
Вероятно вы заметили, что выходной сигнал всегда равен самой левой входной колонке. Таким образом ответ будет 1.
Процесс обучения нейронной сети
Как же должно происходить обучение нашего нейрона, чтобы он смог ответить правильно? Мы добавим каждому входу вес, который может быть положительным или отрицательным числом. Вход с большим положительным или большим отрицательным весом сильно повлияет на выход нейрона. Прежде чем мы начнем, установим каждый вес случайным числом. Затем начнем обучение:
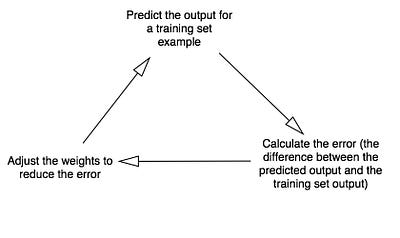
В конце концов вес нейрона достигнет оптимального значения для тренировочного набора. Если мы позволим нейрону «подумать» в новой ситуации, которая сходна с той, что была в обучении, он должен сделать хороший прогноз.
Формула для расчета выхода нейрона
Вам может быть интересно, какова специальная формула для расчета выхода нейрона? Сначала мы берем взвешенную сумму входов нейрона, которая:
Затем мы нормализуем это, поэтому результат будет между 0 и 1. Для этого мы используем математически удобную функцию, называемую функцией Sigmoid:
Если график нанесен на график, функция Sigmoid рисует S-образную кривую.
Подставляя первое уравнение во второе, получим окончательную формулу для выхода нейрона:
Возможно, вы заметили, что мы не используем пороговый потенциал для простоты.
Формула для корректировки веса
Во время тренировочного цикла (Диаграмма 3) мы корректируем веса. Но насколько мы корректируем вес? Мы можем использовать формулу «Взвешенная по ошибке» формула
Почему эта формула? Во-первых, мы хотим сделать корректировку пропорционально величине ошибки. Во-вторых, мы умножаем на входное значение, которое равно 0 или 1. Если входное значение равно 0, вес не корректируется. Наконец, мы умножаем на градиент сигмовидной кривой (диаграмма 4). Чтобы понять последнее, примите во внимание, что:
Градиент Сигмоды получается, если посчитать взятием производной:
Вычитая второе уравнение из первого получаем итоговую формулу:
Существуют также другие формулы, которые позволяют нейрону учиться быстрее, но приведенная имеет значительное преимущество: она простая.
Написание Python кода
Хоть мы и не будем использовать библиотеки с нейронными сетями, мы импортируем 4 метода из математической библиотеки numpy. А именно:
Например, мы можем использовать array() для представления обучающего множества, показанного ранее.
“.T” — функция транспонирования матриц. Итак, теперь мы готовы для более красивой версии исходного кода. Заметьте, что на каждой итерации мы обрабатываем всю тренировочную выборку одновременно.
Код также доступен на гитхабе. Если вы используете Python3 нужно заменить xrange на range.
Заключительные мысли
Попробуйте запустить нейросеть, используя команду терминала:
Итоговый должен быть похож на это:
У нас получилось! Мы написали простую нейронную сеть на Python!
Сначала нейронная сеть присваивала себе случайные веса, а затем обучалась с использованием тренировочного набора. Затем нейросеть рассмотрела новую ситуацию [1, 0, 0] и предсказала 0.99993704. Правильный ответ был 1. Так очень близко!
Традиционные компьютерные программы обычно не могут учиться. Что удивительного в нейронных сетях, так это то, что они могут учиться, адаптироваться и реагировать на новые ситуации. Так же, как человеческий разум.
Конечно, это был только 1 нейрон, выполняющий очень простую задачу. А если бы мы соединили миллионы этих нейронов вместе?
Пишем свою нейросеть: пошаговое руководство
Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.

В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.
1 Что такое искусственная нейросеть?
Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.
2 Структура ИНС
2.1 Искусственный нейрон
Которая выглядит следующим образом:
2.2 Узлы
Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.
Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.
Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:
где wi— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.
2.3 Смещение
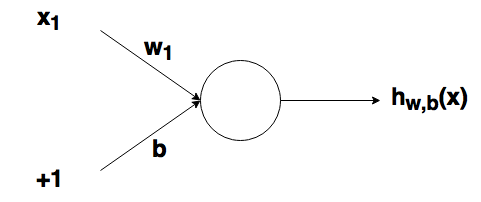
Рассмотрим простой узел, в котором есть по одному входу и выходу:
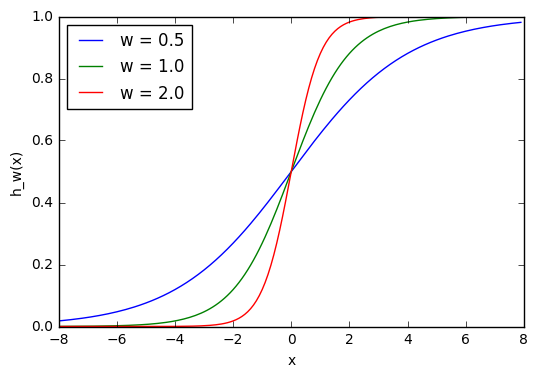
Ввод для активационной функции в этом узле просто x1w1. На что влияет изменение в w1 в этой простой сети?
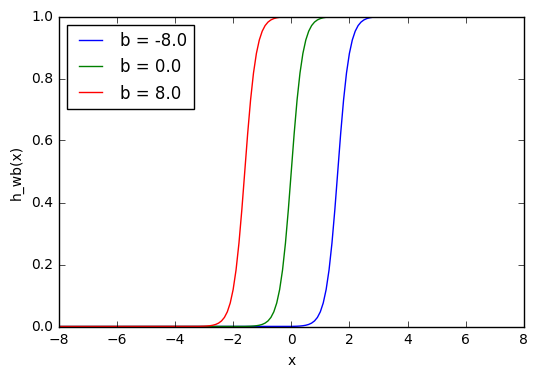
Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:
Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.
2.4 Составленная структура
Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:
2.5 Обозначение
3 Процесс прямого распространения
Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:
3.1 Пример прямого распространения
Представим эту матрицу через массивы библиотеки numpy.
Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:
Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:
Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:
3.2 Первая попытка реализовать процесс прямого распространения
Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.
Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:
возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:
3.3 Более эффективная реализация
В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.
3.4 Векторизация в нейронных сетях
, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:
Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:
3.5 Умножение матриц
Распишем z (l+1) =W (l) h (l) +b (l) на выражение из матрицы и векторов входного слоя ( h (l) =x):
Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.
Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:
Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.
Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.
На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.
4 Градиентный спуск и оптимизация
Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L 1 (Это будет рассмотрено позже).
y (1) в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0. 0)для буквы а, (0,1. 0) для буквы б и т. д.
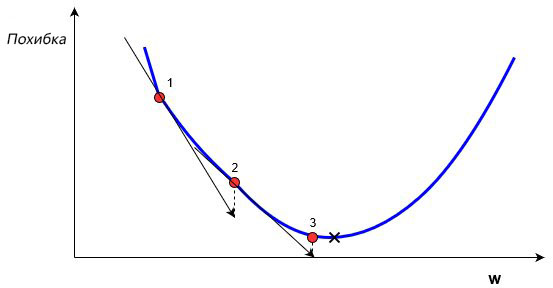
В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:
На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.
Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:
, где wн означает новое значение w, wст— текущее или «старое» значение w, ∇error является градиентом погрешности на wст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.
4.1 Простой пример на коде
Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.
4.2 Функция оценки
Выражение является функцией оценки учебного экземпляра zth, где h (nl) является выходом последнего слоя, то есть выход нейронной сети. h (nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L 2 погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(x z )-y z ), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.
Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:
Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.
4.3 Градиентный спуск в нейронных сетях
Градиентный спуск для каждого веса w(ij) (l) и смещение bi(l) в нейронной сети выглядит следующим образом:
Значения ∂/∂wij (l) и ∂/∂bi (l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.
4.4 Пример двумерного градиентного спуска
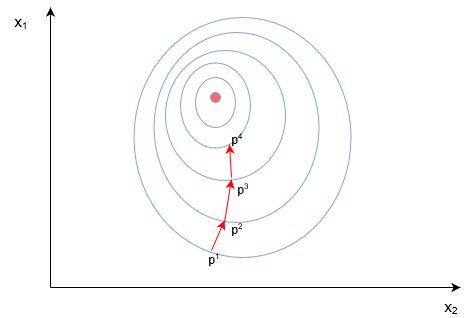
Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:
Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x1 в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).
Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.
4.5 Углубляемся в обратное распространение
Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.
Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:
Выход этой нейронной сети находится по формуле:
Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z1 (2) /∂w12 (2) :
здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:
Мы выяснили, как находить ∂J/∂w12 (2) по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:
, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:
, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.
4.6 Распространение в скрытых слоях
Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(yi-hi (nl) )имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.
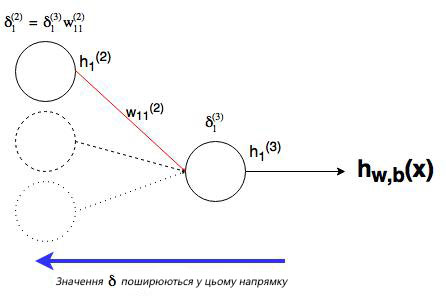
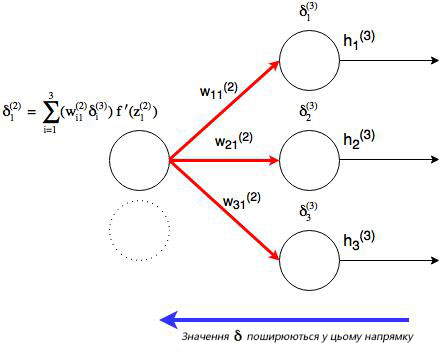
Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:
, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δj (l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:
Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:
Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.
4.7 Векторизация обратного распространения
Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):
Используя операцию трансформирования, мы можем достичь результата, который нам нужен.
Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:
символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W (l) ) T δ(l+1))требует еще одного сложения весов и значений δ.
4.8 Реализация этапа градиентного спуска
Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:
Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):
4.9 Конечный алгоритм градиентного спуска
Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.
Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.
5 Имплементация нейросети языке Python
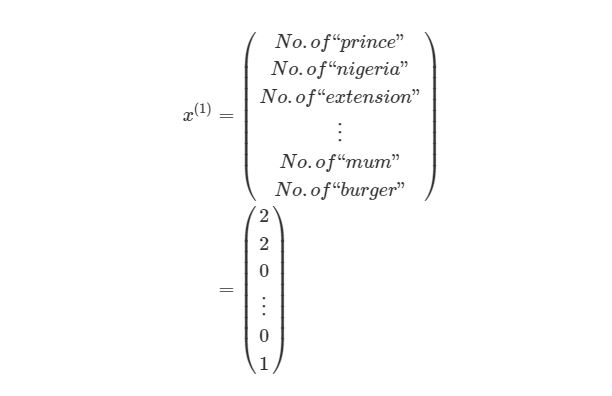
Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:
01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.
5.1 Масштабирование данных
Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:
Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:
5.2 Создание тестов и учебных наборов данных
Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:
5.3 Настройка выходного слоя
В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:
Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].
5.4 Создаем нейросеть
Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:
Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W (l) Когда итерация (l) б. Найдите значение δ ( nl) выходного слоя. Обновите ΔW (l) и Δb ( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:
Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через <>). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:
Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)
Далее запустим процесс прямого распространения через нейронную сеть:
И наконец, найдем выходной слой δ (nl) и значение δ (l) в скрытых слоях для запуска обратного распространения:
Теперь мы можем соединить все этапы в одну функцию:
И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:
После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.
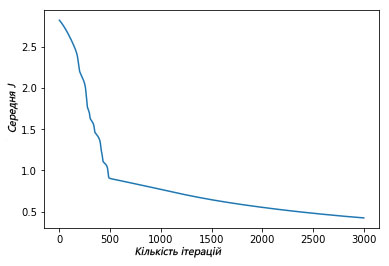
Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:
Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.
5.5 Оценка точности модели
Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:
Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.