Слово Как написать основание логарифма в калькуляторе - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Вычисление логарифма числа онлайн

Знаков после запятой:

Онлайн калькулятор логарифмов

Калькулятор вычисляет логарифм числа онлайн. Можно вводить как десятичные дроби (в качестве разделителя для десятичных дробей можно использовать как точку, так и запятую), так и обычные (например, если нужно вычислить логарифм то в поле «число» можете смело писать 1/9).

Помните, что операция взятия логарифма определена только для положительных чисел, а основание логарифма должно быть положительным и не должно равняться единице.

Что такое логарифм числа?

Это равенство называют основным логарифмическим тождеством.

Примеры

Решение. По определению, равен показателю степени, в которую нужно возвести число чтобы получить число Так как то эта степень равна двум. То есть

Видно, что для вычисления этого логарифма никакой калькулятор не нужен!

Так как то

Как видите, всё не так уж сложно!

На этом всё интересное о логарифмах не заканчивается, поэтому в продолжение этой статьи любознательным читателям рекомендуем прочитать о свойствах логарифмов.

Источник

Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов

Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.

Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.

В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.

Итак, давайте разбираться, что такое логарифм.

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Основные свойства логарифмов

Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:

Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!

Рассмотрим свойства логарифмов на примерах.

Логарифмический ноль и логарифмическая единица

Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.

Запомните, что логарифм от a по основанию а всегда равен единице:

log_a a = 1 – это логарифмическая единица.

Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:

log_a 1 = 0 – логарифмический ноль.

Основное логарифмическое тождество

В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.

Вторая формула по сути является просто переформулированным определением логарифма

Разберем применение тождества на примере:

Необходимо найти значение выраженияСначала преобразуем логарифм

Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:

10 примеров логарифмов с решением

1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник

Как вводить данные? Правила ввода

Ввод данных, наверное, это самое главное, что необходимо усвоить при работе с математическими калькуляторами по решению задач. Не важно какие сервисы вы используете, будь то сайт, десктопная программа или мобильное приложение, ведь именно с корректного ввода данных начинается постановка задачи для вычислительной системы.

Как правило у каждого подобного сервиса свой синтаксис. Но какими бы ни были современные математические калькуляторы (программы), в любом случае все они базируются на принципах обработки, которые появились еще в прошлом веке. Отличаются лишь методы обработки (парсинг математических выражений), но математические формулы от этого, разумеется, не меняются.

Стоит отметить, что калькуляторы на Math24.biz куда более «умнее», или, иными словами, менее требовательны, чем ряд других аналогичных калькуляторов на просторах интернета.

Итак, начнем. Самые элементарные правила как вводить данные касаются записи чисел и скобок.

Скобки используются круглые. Но даже если вы введете [, ], <или >, то они преобразуются в соответствующие круглые. Кстати, это небольшое наше преимущество в отличие от других калькуляторов.

Обратим внимание на записи десятичных чисел и некоторых математических констант. В десятичной записи числа необходимо использовать точку, а не запятую.

Примеры ввода десятичных чисел

Такое правило ввода данных оправдывается тем, что запятая используется в функциях, например, логарифмических, в которых разделены через запятую основание логарифма и число, от которого берется логарифм. И таких функций множество, включая функции нескольких переменных.

Примеры обозначений математических констант

Корень квадратный от числа записывается как sqr или sqrt.

Примеры записи квадратного корня

Наверняка многие сейчас подумали, что квадратный корень из 2 можно записать как 2^(1/2) или 2^(0.5). Но в данном случае мы хотим лишь сказать, что sqrt есть обозначение квадратного корня, которое используется во многих программах.

Примите это на заметку, если ранее не встречались с этим обозначением!

Далее быстро пройдемся по математическим операциям и правилам их ввода, потому что здесь всё проще-простого.

+ Операция сложения (суммирование)
− Операция вычитания (разность)
* Операция умножения

Кстати, если два множителя записать через пробел, то калькулятор воспримет это за знак умножения. Например, x y равносильно x*y

/ Операция деления
^ Возведение в степень

Чуть сложнее для визуального восприятия, но никак не для понимания, это правило записи дробных выражений. Как вводить данные от таких выражений мы покажем на примерах с применением различных цветов.

Это позволит лучше и быстрее освоить необходимые навыки юным ученикам. Хотя, поверьте нам, старшеклассники и студенты очень часто сталкиваются с проблемой ввода сложных формул.

Примеры ввода дробных выражений

Для лучшего визуального восприятия мы специально добавили пробелы, чтобы выделить отдельные операции.

( (z-1) (t+1) ) / ( (x-1) / (y+1) )

Как вы могли заметить, одним из базовых правил при вводе данных является использование букв только латинского алфавита!

Ниже перечислим наиболее часто встречающиеся функции при изучении школьной математики и математических дисциплин начальных курсов ВУЗов и других учебных заведений.

Источник

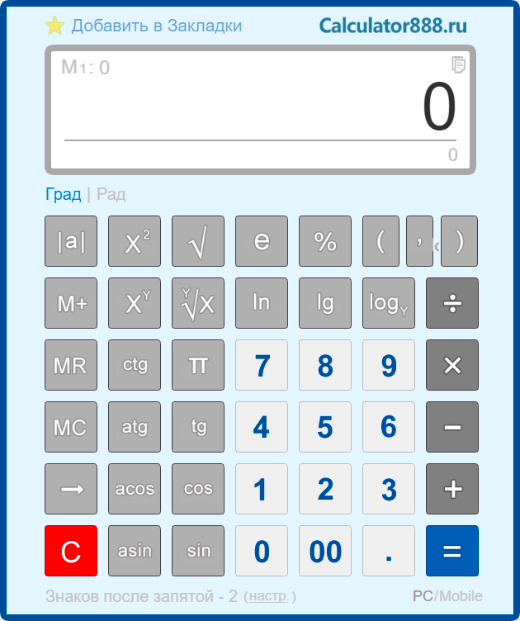
Работа с инженерным калькулятором

Калькулятор инженерный

Используйте инженерный калькулятор для сложных расчетов с применением тригонометрических функций. Команды вводятся с помощью мыши или клавиатуры.
Инженерный калькулятор позволяет производить сложные расчеты с применением различных тригонометрических функций: синуса, косинуса, тангенса, котангенса. Калькулятор позволяет возводить числа в степень, вычислять логарифм числа.
Основные команды (цифры, умножение, деление, сложение, вычитание, равенство, сброс) можно вводить как с помощью мышки, так и с помощью цифровой клавиатуры (верхней или боковой). Подробные инструкции по работе с инженерным калькулятором смотрите внизу страницы.

Функции стандартных кнопок

Ввод команд с компьютерной клавиатуры

Для работы с калькулятором можно использовать любые цифровые клавиши: как цифровые клавиши находящиеся сверху, так и отдельные цифровые клавиши находящиеся справа.

Для ввода равно можно использовать клавишу [ Enter ];
Для стирания последнего знака используется клавиша [ Backspace ] (клавиша со стрелкой);
Для ввода знака плюс используется клавиша [ + ] сверху или на боковой клавиатуре;
Для ввода знака минус используется клавиша [ – ] сверху или на боковой клавиатуре;
Для ввода знака умножения используется клавиша [ * ] на боковой клавиатуре;
Для ввода знака деления используется клавиша [ / ] на боковой клавиатуре;
Для сброса калькулятора можно использовать клавиши [ Esc ], [ Del ] на верхней клавиатуре или [ End ] на цифровой клавиатуре.

Примеры вычислений на инженерном калькуляторе

Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.

Только корректные расчеты по всем правилам математики!

В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.

Всё для вашего удобства:

Содержание справки:

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

Инструкция по функциям инженерного калькулятора

Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце – знак равенства.

Как пользоваться MR MC M+ M- MS

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:

12 [x y ] 3 [=]

12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]

Как найти корень кубический

Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:

729 [3√x] [=]

729, [ 3 √x] «кубический корень из икс», равенства [=]

Как найти корень на калькуляторе

Задача: Найти квадратный корень 36.

Решение: всё просто, нажимаем так:

36 [ y √x] 2 [=]

36, [ y √x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]

При помощи этой функции вы можете найти корень в любой степени, не только квадратный.

Как возвести в квадрат

Для возведения в квадрат онлайн вычислительная программа содержит две функции:

[x y ] «икс в степени игрик», [X 2 ] «икс в квадрате»

Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 [x y ] 6 [=]

Ответ: сорок пять в шестой степ. равно 8303765625

Тригонометрический калькулятор онлайн – примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

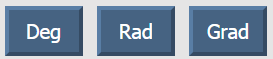
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad – в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90 [sin] [=]

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60 [cos] [=]

Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 [Deg] [=] 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1 [log] [=]

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100 [log] [=]

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм – log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой [ln].

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145 [MR]

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

Из этой статьи вы узнаете, как пользоваться основными функциями научного (инженерного) калькулятора. Научный калькулятор пригодится при изучении алгебры, геометрии и тригонометрии.

Найдите основные функции. На калькуляторе есть несколько функций, которые понадобятся для решения алгебраических, тригонометрических, геометрических и других задач. Найдите на калькуляторе следующие функции:

Источник