Арифметические операторы (справочник по C#)
Следующие операторы выполняют арифметические операции с операндами числовых типов:
Эти операторы поддерживаются всеми целочисленными типами и типами с плавающей запятой.
Оператор инкремента ++
Оператор инкремента ++ увеличивает операнд на 1. Операндом должна быть переменная, свойство или индексатор.
Оператор инкремента поддерживается в двух формах: постфиксный оператор инкремента ( x++ ) и префиксный оператор инкремента ( ++x ).
Постфиксный оператор приращения
Результатом x++ является значение x перед выполнением операции, как показано в следующем примере:
Префиксный оператор инкремента
Результатом ++x является значение x после выполнения операции, как показано в следующем примере:
Постфиксный оператор уменьшения
Результатом x— является значение x перед выполнением операции, как показано в следующем примере:
Префиксный оператор декремента
Операторы унарного плюса и минуса
Оператор умножения *
Оператор умножения * вычисляет произведение операндов:
Оператор деления /
Оператор деления / делит левый операнд на правый.
Деление целых чисел
Для операндов цельночисленных типов результат оператора / является целочисленным типом, который равен частному двух операндов, округленному в сторону нуля:
Деление чисел с плавающей запятой
Оператор остатка %
Оператор остатка % вычисляет остаток от деления левого операнда на правый.
Целочисленный остаток
Используйте метод Math.DivRem для вычисления результатов как целочисленного деления, так и определения остатка.
Остаток с плавающей запятой
Этот метод вычисления остатка аналогичен тому, который использовался для целочисленных операндов, но отличается от спецификации IEEE 754. Если вам нужна операция вычисления остатка, которая соответствует спецификации IEEE 754, используйте метод Math.IEEERemainder.
Сведения о поведение оператора % в случае неконечных операндов см. в разделе Оператор остаткаспецификации языка C#.
Для операндов decimal оператор остатка % эквивалентен оператору остатка типа System.Decimal.
В следующем примере показано поведение оператора остатка для операндов с плавающей запятой:
Оператор сложения +
Оператор сложения + вычисляет сумму своих операндов:
Составное присваивание
Для бинарного оператора op выражение составного присваивания в форме
за исключением того, что x вычисляется только один раз.
Следующий пример иллюстрирует использование составного присваивания с арифметическими операторами:
Приоритет и ассоциативность операторов
В следующем списке перечислены арифметические операторы в порядке убывания приоритета:
Бинарные арифметические операторы имеют левую ассоциативность. То есть операторы с одинаковым приоритетом вычисляются в направлении слева направо.
Порядок вычисления, определяемый приоритетом и ассоциативностью операторов, можно изменить с помощью скобок ( () ).
Полный список операторов C#, упорядоченный по уровню приоритета, можно найти в разделе Приоритет операторов статьи Операторы C#.
Арифметическое переполнение и деление на нуль
Если результат арифметической операции выходит за пределы диапазона возможных конечных значений соответствующего числового типа, поведение арифметического оператора зависит от типа его операндов.
Целочисленное арифметическое переполнение
Деление целого числа на ноль всегда вызывает исключение DivideByZeroException.
В случае целочисленного арифметического переполнения итоговое поведение определяется контекстом проверки переполнения, который может быть проверяемым или непроверяемым:
По умолчанию арифметические операции выполняются в непроверяемом контексте.
Арифметическое переполнение с плавающей запятой
Арифметические операции с типами float и double никогда не вызывают исключение. Результатом арифметических операций с этими типами может быть одно из специальных значений, представляющих бесконечность и объект, не являющийся числовым:
Для операндов типа decimal арифметическое переполнение всегда вызывает исключение OverflowException, а деление на нуль всегда вызывает исключение DivideByZeroException.
Ошибки округления
Из-за общих ограничений, касающихся представления вещественных чисел в форме с плавающей запятой и арифметических операций с плавающей запятой, при вычислениях с использованием типов с плавающей запятой могут возникать ошибки округления. То есть полученный результат выражения может отличаться от ожидаемого математического результата. В следующем примере показано несколько таких случаев:
См. заметки в справочной документации по System.Double, System.Single и System.Decimal.
Возможность перегрузки оператора
Спецификация языка C#
Дополнительные сведения см. в следующих разделах статьи Спецификация языка C#:
Как возвести число в степень в си шарп
Как возвести число в степень в си шарп
В Unity (C#) для возведения в степень есть функция:
Данная функция возвращает значение n в степени p.
Для возведения в степень экспоненты в Unity (C#) есть отдельная функция:
Логарифмы
Вычисление логарифма в Unity (C#) производиться через функцию:
Вернёт 2.
Для получения натурального логарифма (основание — экспонента) в Unity (C#) достаточно не указывать основание:
Быстрое возведение в степень
Быстрое возведение в степень – это алгоритм, который позволяет возвести любое число в натуральную степень за сокращенное количество умножений.
Описание алгоритма
Для любого числа x и четной степени n выполняется тождество:
x n = (x n/2 ) 2 = x n/2 ⋅ x n/2
Это и является основой алгоритма быстрого возведения в степень. Поскольку такое разбиение позволяет, за одну операцию умножения, вдвое уменьшить вычисляемую степень.
Для случая нечетной степени, достаточно её понизить на единицу:
x n = x n — 1 ⋅ x, при этом (n — 1) четное число.
Рекурсивная реализация быстрого возведения в степень
Для оптимизации можно заменить проверку четности и деление на 2 битовыми операциями:
Итерационная реализация
В этом методе, быстрого возведения в степень, также используем оптимизацию проверки на четность и деления на два:
Ускоряем pow
В этой статье я хочу поделиться несколькими нестандартными алгоритмами для быстрого возведения числа в степень, а также продемонстрировать их реализацию и сравнить их быстродействие в C++, C# и Java.
Сравнить точность алгоритмов можно прямо сейчас на этой странице.
В конце будет краткая памятка по тому, где и когда лучше применять какой из методов. При правильном выборе можно добиться увеличения скорости вычислений в 5 раз при погрешности
1%, а иногда и вовсе без неё.
Содержание
На повестке дня у нас есть 5 алгоритмов: «Старая аппроксимация», «Бинарная степень», «Делящая быстрая степень», «Дробная” быстрая степень» и «Другая” аппроксимация».
Названия алгоритмам я придумал сам (за исключением бинарной степени), так как нигде не нашёл официальных версий, но вы можете называть их иначе.
Для расчета прироста скорости и погрешности будем сравнивать эти методы со стандартными функциями pow, Math.Pow и Math.pow в C++, C# и Java соответственно. О том, как производилось сравнение, будет сказано в частях “Сравнение производительности” и “Сравнение точности”.
Алгоритм: «Старая аппроксимация»
Увеличение скорости: в
e = 1012 — последний 1 → v *= b → v = 2
b *= b → b = 4
e >>= 1 → e = 102 = 2
e = 102 — последний 0 → пропускаем
b *= b → b = 16
e >>= 1 → e = 1
e = 12 — последний 1 → v *= b → v = 32
.
e = 0 → выход из цикла
Алгоритм: «Делящая быстрая степень»
Увеличение скорости: в
13%
Примечание: в коде ниже присутствуют проверки для особых входных данных. Без них код работает всего на 10% быстрее, но погрешность возрастает в десятки раз (особенно при использовании отрицательных степеней).
Реализация в C# и Java
Мы разбиваем степень на две части: e / el, которая всегда меньше или равна 1, и el, которая является целым числом. Теперь для расчета x^(e / el) мы можем использовать “старую” аппроксимацию, а для x^el — бинарную степень.Таким образом, объединяя этих два узкоспециализированных метода, мы получили универсальный метод. Но эту идею можно реализовать по-другому.
Алгоритм: «Дробная быстрая степень»
Увеличение скорости: в
Реализация в C# и Java
По сути, любое число состоит из суммы двух частей: целой и дробной. Целую можно использовать для возведения основания в степень при помощи бинарного возведения, а дробную — при помощи “старой” аппроксимации.
В результате получаем следующую формулу:
Она, в отличии от формулы “делящего” метода, никак не искажает дробную часть. Это позволяет добиться намного большей точности.
Ускоряем pow
В этой статье я хочу поделиться несколькими нестандартными алгоритмами для быстрого возведения числа в степень, а также продемонстрировать их реализацию и сравнить их быстродействие в C++, C# и Java.
Сравнить точность алгоритмов можно прямо сейчас на этой странице.
В конце будет краткая памятка по тому, где и когда лучше применять какой из методов. При правильном выборе можно добиться увеличения скорости вычислений в 5 раз при погрешности
1%, а иногда и вовсе без неё.
Содержание
На повестке дня у нас есть 5 алгоритмов: «Старая аппроксимация», «Бинарная степень», «Делящая быстрая степень», «Дробная” быстрая степень» и «Другая” аппроксимация».
Названия алгоритмам я придумал сам (за исключением бинарной степени), так как нигде не нашёл официальных версий, но вы можете называть их иначе.
Для расчета прироста скорости и погрешности будем сравнивать эти методы со стандартными функциями pow, Math.Pow и Math.pow в C++, C# и Java соответственно. О том, как производилось сравнение, будет сказано в частях “Сравнение производительности” и “Сравнение точности”.
Алгоритм: «Старая аппроксимация»
Увеличение скорости: в
11 раз
Погрешность: Реализация в C# и Java
Разработчики для этого написали такую функцию
Узнал я об этом методе из статьи «Магическая константа» 0x5f3759df. В ней подробно объясняется как работает этот код и как его можно улучшить для работы с любой степенью и double’ми вместо float’ов. В моих кодах также есть магическая константа 4606853616395542500L. Нашёл я её по следующей формуле (она описана в статье выше):
Число 1.0730088 было подобрано вручную для достижения наибольшей точности вычислений.
Алгоритм: Бинарное возведение в степень
Увеличение скорости: в среднем в
7.5 раз, преимущество сохраняется до возведения чисел в степень 134217728 в C++/C# и 4096 в Java.
Погрешность: нет, но стоит отметить, что операция умножения не ассоциативна для чисел с плавающей точкой, т.е. 1.21 * 1.21 не то же самое, что 1.1 * 1.1 * 1.1 * 1.1, однако при сравнении со стандартными функциями погрешности, как уже сказано ранее, не возникает.
Ограничения: степень должна быть целым числом не меньше 0
Реализация в C# и Java
Алгоритм: «Делящая быстрая степень»
Увеличение скорости: в
13%
Примечание: в коде ниже присутствуют проверки для особых входных данных. Без них код работает всего на 10% быстрее, но погрешность возрастает в десятки раз (особенно при использовании отрицательных степеней).
Реализация в C# и Java
Алгоритм: «Дробная быстрая степень»
Увеличение скорости: в
Реализация в C# и Java
В результате получаем следующую формулу:
Она, в отличии от формулы “делящего” метода, никак не искажает дробную часть. Это позволяет добиться намного большей точности.
Алгоритм: «Другая аппроксимация»
Увеличение скорости: в
9 раз
Погрешность: Реализация в C# и Java
Про историю этого алгоритма я ничего не знаю, я просто нашёл его тут: Optimized pow() approximation for Java, C / C++, and C#. Возможно, если использовать его в “делящей–” и “дробной быстрых степенях» вместо “старой” аппроксимации, можно достигнуть лучшей точности ценой немного меньшей скорости.
Сравнение производительности
Псевдокод сравнения производительности в C++:
Аналогично измерялась скорость в C# и Java. В репозитории проекта можно посмотреть на реальный код для сравнения производительности в C++, C# и Java.
Тесты производились в каждом языке для степеней в промежутках [-10.5, 0], [0, 2], [0, 10.5], [0, 25.75], [0, 55.5]. Прирост скорости каждого метода по сравнению со стандартным в каждом языке для каждого сета степеней изображен на графиках ниже:


Рассмотреть подробнее результаты тестов можно посмотреть в этой таблице.
Тесты проводились на i5-10300H, 19.8 DDR4 GB usable RAM, 64-битная платформа.
C++: MSVC + /O2 + /Oi + /Ot
C#: optimize code
Сравнение точности
Для рассчитывания точности я возводил очередное число в определенную степень стандартным и одним из нестандартных способами, потом делил большее из полученных чисел на меньшее, складывал все эти отношения вместе, а в конце делил их на количество сравнений. Так и получалось значение погрешности.
Основания и степени генерировались также, как и в алгоритме сравнения производительности.
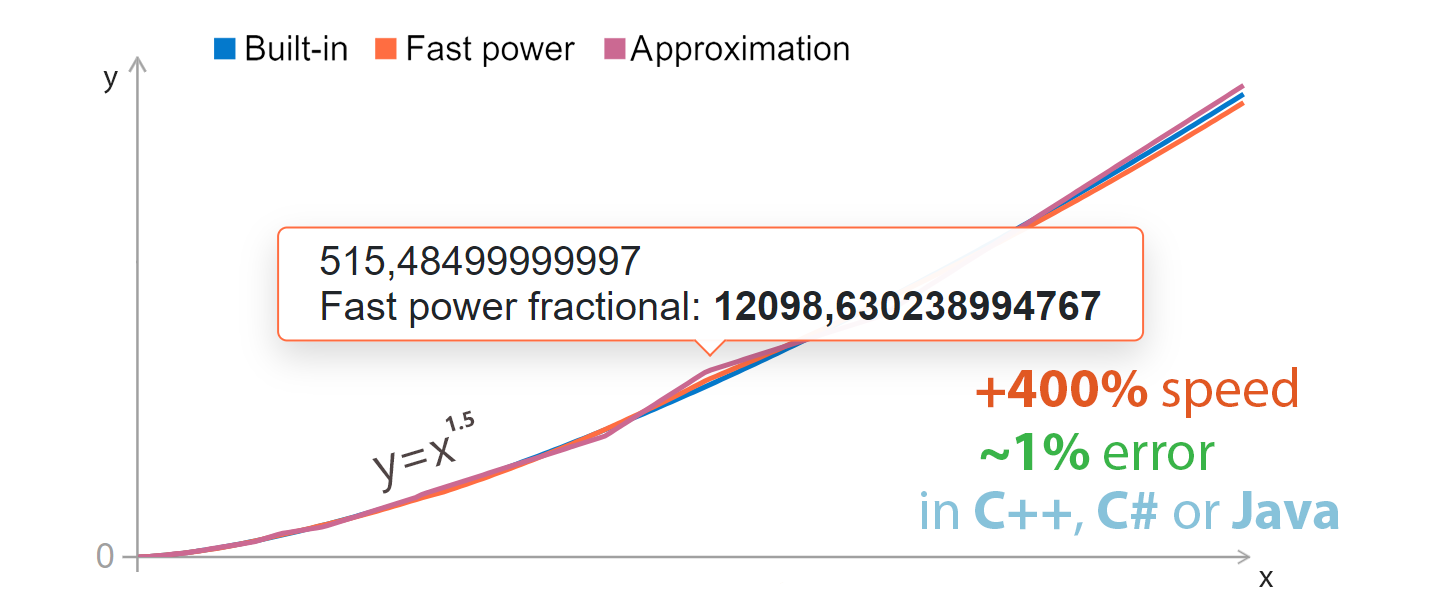
Для более гибкого и удобного тестирования я создал Blazor страницу, на которой можно построить графики реальных и полученных одним из методов значений чисел, лежащих в заданном промежутке и возведенных в указанную степень:
Ниже на этой же странице можно самим провести сравнение точности каждого метода для всех степеней, лежащих в заданном промежутке:
Вывод
Каждый из перечисленных мною методов дает различную точность и скорость. Поэтому, прежде чем использовать стандартную функцию возведения в степень, стоит проанализировать какие у вас будут входные данные, и насколько вам важна точность. Выбор правильного метода может существенно ускорить работу вашей программы. Чтобы сделать этот процесс проще, я подготовил вот такую шпаргалку:
Код всего проекта доступен на гитхабе. Там вы найдете и реализации всех алгоритмов в трех языках, и программы для сравнения точности для каждого языка, и код сайта.
Спасибо за внимание. Надеюсь эта статья поможет сделать ваш код немного быстрее.
Math Класс
Определение
Некоторые сведения относятся к предварительной версии продукта, в которую до выпуска могут быть внесены существенные изменения. Майкрософт не предоставляет никаких гарантий, явных или подразумеваемых, относительно приведенных здесь сведений.
Предоставляет константы и статические методы для тригонометрических, логарифмических и иных общих математических функций.
Примеры
В следующем примере Math для вычисления внутренних углов трапеции используются несколько математических и тригонометрических функций класса.
Представляет отношение длины окружности к ее диаметру, определяемое константой π.
Представляет число радианов в полном обороте, заданное константой τ.
Методы
Возвращает абсолютное значение числа Decimal.
Возвращает абсолютное значение числа двойной точности с плавающей запятой.
Возвращает абсолютное значение 16-битового целого числа со знаком.
Возвращает абсолютное значение 32-битового целого числа со знаком.
Возвращает абсолютное значение 64-битового целого числа со знаком.
Возвращает абсолютное значение собственного целого числа со знаком.
Возвращает абсолютное значение 8-битового целого числа со знаком.
Возвращает абсолютное значение числа одинарной точности с плавающей запятой.
Возвращает угол, косинус которого равен указанному числу.
Возвращает угол, гиперболический косинус которого равен указанному числу.
Возвращает угол, синус которого равен указанному числу.
Возвращает угол, гиперболический синус которого равен указанному числу.
Возвращает угол, тангенс которого равен указанному числу.
Возвращает угол, тангенс которого равен отношению двух указанных чисел.
Возвращает угол, гиперболический тангенс которого равен указанному числу.
Умножает два 32-битовых числа.
Формирует полное произведение двух 64-битовых чисел.
Формирует полное произведение двух 64-битовых чисел без знака.
Возвращает кубический корень из указанного числа.
Возвращает наименьшее целое число, которое больше или равно заданному десятичному числу.
Возвращает наименьшее целое число, которое больше или равно заданному числу с плавающей запятой двойной точности.
Возвращает косинус указанного угла.
Возвращает гиперболический косинус указанного угла.
Создает частное и остаток от двух 8-разрядных чисел без знака.
Создает частное и остаток от двух 16-разрядных чисел со знаком.
Создает частное и остаток от двух 32-разрядных чисел со знаком.
Вычисляет частное двух 32-разрядных знаковых целых чисел и возвращает остаток в выходном параметре.
Создает частное и остаток от двух 64-разрядных чисел со знаком.
Вычисляет частное двух 64-битовых целых чисел со знаком и возвращает остаток в выходном параметре.
Создает частную и оставшуюся часть двух чисел со знаком в собственном формате.
Создает частное и остаток от двух 8-разрядных чисел со знаком.
Создает частное и остаток от двух 16-разрядных чисел без знака.
Создает частную и оставшуюся часть двух неподписанных 32-разрядных чисел.
Создает частную и оставшуюся часть двух неподписанных 64-разрядных чисел.
Создает частное и остаток от двух неподписанных чисел в собственном формате.
Возвращает наибольшее целое число, которое меньше или равно указанному десятичному числу.
Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности.
Возвращает значение (x * y) + z, округленное в рамках одной тернарной операции.
Возвращает остаток от деления одного указанного числа на другое указанное число.
Возвращает целочисленный логарифм с основанием 2 указанного числа.
Возвращает натуральный логарифм (с основанием e ) указанного числа.
Возвращает логарифм указанного числа в системе счисления с указанным основанием.
Возвращает логарифм с основанием 10 указанного числа.
Возвращает логарифм с основанием 2 указанного числа.
Возвращает большее из двух 8-битовых целых чисел без знака.
Возвращает большее из двух десятичных чисел.
Возвращает большее из двух чисел двойной точности с плавающей запятой.
Возвращает большее из двух 16-битовых целых чисел со знаком.
Возвращает большее из двух 32-битовых целых чисел со знаком.
Возвращает большее из двух 64-битовых целых чисел со знаком.
Возвращает большее из двух собственных целых чисел со знаком.
Возвращает большее из двух 8-битовых целых чисел со знаком.
Возвращает большее из двух чисел одинарной точности с плавающей запятой.
Возвращает большее из двух 16-битовых целых чисел без знака.
Возвращает большее из двух 32-битовых целых чисел без знака.
Возвращает большее из двух 64-битовых целых чисел без знака.
Возвращает большее из двух собственных беззнаковых целых чисел.
Возвращает большую величину из двух чисел двойной точности с плавающей запятой.
Возвращает меньшее из двух 8-битовых целых чисел без знака.
Возвращает меньшее из двух десятичных чисел.
Возвращает меньшее из двух чисел двойной точности с плавающей запятой.
Возвращает меньшее из двух 16-битовых целых чисел со знаком.
Возвращает меньшее из двух 32-битовых целых чисел со знаком.
Возвращает меньшее из двух 64-битовых целых чисел со знаком.
Возвращает меньшее из двух собственных целых чисел со знаком.
Возвращает меньшее из двух 8-битовых целых чисел со знаком.
Возвращает меньшее из двух чисел одинарной точности с плавающей запятой.
Возвращает меньшее из двух 16-битовых целых чисел без знака.
Возвращает меньшее из двух 32-битовых целых чисел без знака.
Возвращает меньшее из двух 64-битовых целых чисел без знака.
Возвращает меньшее из двух собственных беззнаковых целых чисел.
Возвращает меньшую величину из двух чисел двойной точности с плавающей запятой.
Возвращает указанное число, возведенное в указанную степень.
Возвращает оценку обратной величины указанного числа.
Возвращает оценку корня обратного квадрата указанного числа.
Округляет десятичное значение до ближайшего целого значения; значения посередине округляются до ближайшего четного числа.
Округляет десятичное значение до указанного числа знаков после запятой; значения посередине округляются до ближайшего четного числа.
Округляет десятичное значение до указанного числа цифр дробной части с использованием указанного соглашения о округлении.
Округляет десятичное значение до целого, используя заданное соглашение о округлении.
Округляет значение с плавающей запятой двойной точности до ближайшего целого значения; значения посередине округляются до ближайшего четного числа.
Округляет значение с плавающей запятой двойной точности до указанного числа знаков после запятой; значения посередине округляются до ближайшего четного числа.
Округляет значение с плавающей запятой двойной точности до указанного числа цифр дробной части с использованием указанного соглашения о округлении.
Округляет значение двойной точности с плавающей запятой до целого, используя указанное соглашение о округлении.
Возвращает значение x * 2^n, вычисленное эффективно.
Возвращает целое число, указывающее знак десятичного числа.
Возвращает целое число, обозначающее знак числа двойной точности с плавающей запятой.
Возвращает целое число, указывающее знак 16-разрядного целого числа со знаком.
Возвращает целое число, указывающее знак 32-разрядного целого числа со знаком.
Возвращает целое число, указывающее знак 64-разрядного целого числа со знаком.
Возвращает целое число, указывающее знак целого числа со знаком размером в собственном формате.
Возвращает целое число, указывающее знак 8-разрядного целого числа со знаком.
Возвращает целое число, обозначающее знак числа с плавающей запятой одиночной точности.
Возвращает синус указанного угла.
Возвращает синус и косинус указанного угла.
Возвращает гиперболический синус указанного угла.
Возвращает квадратный корень из указанного числа.
Возвращает тангенс указанного угла.
Возвращает гиперболический тангенс указанного угла.
Вычисляет целую часть заданного десятичного числа.
Вычисляет целую часть заданного числа двойной точности с плавающей запятой.
Операторы и выражения для доступа к элементам (справочник по C#)
При получении доступа к элементу типа можно использовать следующие операторы и выражения:
Выражение доступа к члену
Оператор индексатора []
Доступ к массиву
В приведенном ниже примере показано, как получить доступ к элементам массива.
Если индекс массива выходит за границы соответствующего измерения массива, возникает исключение IndexOutOfRangeException.
Как показано в предыдущем примере, квадратные скобки также используются в объявлении типа массива и для создания экземпляров массива.
Дополнительные сведения см. в руководстве по работе с массивами.
Доступ к индексатору
Индексаторы позволяют индексировать экземпляры определяемого пользователем типа аналогично индексации массива. В отличие от индексов массива, которые должны быть целым числом, параметры индексатора могут быть объявлены любым типом.
Другие данные об использовании []
Сведения о доступе к элементу указателя см. в разделе, посвященном оператору доступа к элементу указателя [], статьи Операторы, связанные с указателем.
Кроме того, с помощью квадратных скобок можно указывать атрибуты.
Если a принимает значение, отличное от NULL, результат a?.x или a?[x] совпадает с результатом a.x или a[x] соответственно.
Если параметр A может быть пустым, а B и C нет, если A не является пустым, необходимо только применить условный оператор NULL к параметру A :
Потокобезопасный вызов делегата
Этот код эквивалентен следующему коду, который будет использоваться в C# 5 или более ранней версии:
Выражения вызова ()
Приведенный ниже пример демонстрирует вызов делегата и метода с аргументами или без них.
Другие данные об использовании ()
Кроме того, с помощью круглых скобок можно настраивать порядок выполнения операций в выражении. Дополнительные сведения см. в разделе Операторы C#.
В выражениях приведения, которые выполняют явные преобразования типов, также используйте круглые скобки.
Индекс от конца: оператор ^
Можно также использовать оператор ^ с оператором диапазона для создания диапазона индексов. См. сведения в руководстве по диапазонам и индексам.
В предыдущем примере выражение a..b имеет тип System.Range. В выражении a..b результаты a и b должны быть неявно преобразованы в int или Index.
Возможность перегрузки оператора
Спецификация языка C#
Дополнительные сведения см. в следующих разделах статьи Спецификация языка C#:
См. сведения о индексах и диапазонах в примечании к функциям.