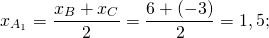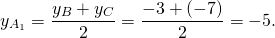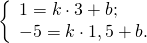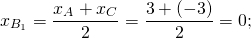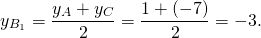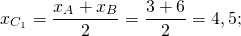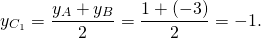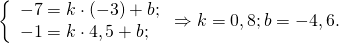Уравнение медианы треугольника
Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
3) Координаты точки C1 — середины отрезка BC:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.