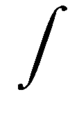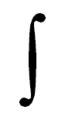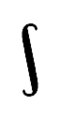Знак интеграла
Знак интеграла используется для обозначения интеграла в математике. Впервые он был использован немецким математиком и основателем дифференциального и интегрального исчислений Лейбницем в конце XVII века.
Символ ( ∫ ) образовался из буквы S (от лат. summa — сумма).
Содержание
Юникод
Кодировка по Unicode, HTML и LaTeX| Знак | Unicode | Название | HTML-представление | LaTeX | |||
|---|---|---|---|---|---|---|---|
| Позиция | Название | Шестнадцатеричное | Десятичное | Мнемоника | |||
| ∫ | U+222B | Integral | Интеграл | ∫ | ∫ | ∫ | \int |
| ∬ | U+222C | Double Integral | Двойной интеграл | ∬ | ∬ | \iint | |
| ∭ | U+222D | Triple Integral | Тройной интеграл | ∭ | ∭ | \iiint | |
| ∮ | U+222E | Contour Integral | Интеграл по контуру | ∮ | ∮ | \oint | |
| ∯ | U+222F | Surface Integral | Интеграл по поверхности | ∯ | ∯ | \oiint (требуется пакет esint) | |
| ∰ | U+2230 | Volume Integral | Интеграл по объёму | ∰ | ∰ | \oiiint (требуется пакет esint) | |
| ∱ | U+2231 | Clockwise Integral | Интеграл с правым обходом | ∱ | ∱ | ||
| ∲ | U+2232 | Clockwise Contour Integral | Интеграл по контуру с правым обходом | ∲ | ∲ | \ointclockwise (требуется пакет esint) | |
| ∳ | U+2233 | Anticlockwise Contour Integral | Интеграл по контуру с левым обходом | ∳ | ∳ | \ointctrclockwise (требуется пакет esint) | |
Традиции начертания
Русскоязычная традиция начертания знака интеграла отличается от принятой в некоторых западных странах.
В англоязычной традиции, реализованной в системе LaTeX, символ существенно наклонён вправо.
Немецкая форма интеграла вертикальна.
В русскоязычной литературе символ выглядит так.
См. также
Ссылки
Литература
Полезное
Смотреть что такое «Знак интеграла» в других словарях:
Знак деления — ÷ Знак деления Пунктуация апостроф (’ ) … Википедия
Знак процента — % Знак процента Пунктуация апостроф (’ … Википедия
Знак радикала — √ Знак корня (знак радикала) в математике условное обозначение для корней, по умолчанию квадратных. В общем случае (для корней n й степени) показатель степени ставится над «птичкой»: знак используется для кубических корней, для корней 4 й степени … Википедия
% (знак) — % % знак, чаще всего обозначающий проценты. Происхождение обозначения … Википедия
Знак умножения — × • Знак умножения (×) математический знак операции умножения. Знак умножения изображают как крестик (×), точку … Википедия
Знак градуса — У этого термина существуют и другие значения, см. Градус. ° Знак градуса Пунктуация апостроф … Википедия
Знак равенства — … Википедия
Знак плюс-минус — У этого термина существуют и другие значения, см. Плюс минус (значения). ± ∓ Знак плюс минус (±) математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и … Википедия
Знак тильда — Тильда (исп. tilde, от лат. titulus надпись) название нескольких типографских знаков в виде волнистой черты. Содержание 1 Диакритический знак 1.1 Надстрочный … Википедия
Знак долготы над гласным — ¯ Макрон (от греч. μακρόν) диакритический знак, изображающийся как черта сверху над символом. В Юникоде макрон в виде комбинирующей диакритики имеет код U+0304, а в виде отдельно стоящего символа U+00AF Употребление В качестве диакритического… … Википедия
Интегралы для чайников: как решать, правила вычисления, объяснение
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
Бари Алибасов и группа
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Свойства определенного интеграла
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Как набирать интегральные символы с клавиатуры?
Интеграл — это математическая функция, используемая в исчислении. Вы можете вводить интегральные уравнения в документы Office с помощью редактора формул. Однако, когда вам просто нужно ввести целые символы, легко использовать сочетания клавиш. В отличие от редактора формул, сочетания клавиш помогают вводить символы, как обычные текстовые символы, выровненные с другим содержимым документа.
Связанный: Сочетания клавиш Alt-кода для математических символов.
Сочетания клавиш для встроенных символов
Ниже приведены различные интегральные символы, доступные в Unicode как часть символов математического оператора между кодовыми точками 2200–22FF.
| Условное обозначение | название | Код Windows | Код Mac |
|---|---|---|---|
| ∫ | интеграл | Alt + 8747 | Вариант + 222B |
| ∬ | Двойной интеграл | Alt + 8748 | Вариант + 222C |
| ∭ | Тройной интеграл | Alt + 8749 | Вариант + 222D |
| ∮ | Contour Integral | Alt + 8750 | Option + 222E |
| ∯ | Поверхностный интеграл | Alt + 8751 | Вариант + 222F |
| ∰ | Объемный интеграл | Alt + 8752 | Вариант + 2230 |
| ∱ | Интеграл по часовой стрелке | Alt + 8753 | Вариант + 2231 |
| ∲ | Контурный интеграл по часовой стрелке | Alt + 8754 | Вариант + 2232 |
| ∳ | Контурный интеграл против часовой стрелки | Alt + 8755 | Вариант + 2233 |
| ⌠ | Верхняя половина Integral | Alt + 8992 | Вариант + 2320 |
| ⌡ | Нижняя половина интегрального | Alt + 8993 | Вариант + 2321 |
| ⎮ | Интегральное расширение | Alt + 9134 | Вариант + 23AE |
| ⨋ | Суммирование с интегралом | Alt + 10763 | Вариант + 2A0B |
| ⨌ | Четверной интегральный оператор | Alt + 10764 | Вариант + 2A0C |
| ⨍ | Конечная часть интеграла | Alt + 10765 | Вариант + 2A0D |
| ⨎ | Интегральный с двойным ходом | Alt + 10766 | Вариант + 2A0E |
| ⨏ | Интегральное среднее с косой чертой | Alt + 10767 | Option + 2A0F |
| ⨕ | Интеграл вокруг точечного оператора | Alt + 10773 | Вариант + 2A15 |
| ⨖ | Кватернионный интегральный оператор | Alt + 10774 | Вариант + 2A16 |
| ⨗ | Интегральный со стрелкой влево с крючком | Alt + 10775 | Вариант + 2A17 |
| ⨘ | Интеграл со знаком времени | Alt + 10776 | Вариант + 2A18 |
| ⨙ | Интеграл с пересечением | Alt + 10777 | Вариант + 2A19 |
| ⨚ | Интеграл с Union | Alt + 10778 | Вариант + 2A1A |
| ⨛ | Интеграл с Overbar | Alt + 10779 | Вариант + 2A1B |
| ⨜ | Интегрально с нижней панелью | Alt + 10780 | Option + 2A1C |
Как набирать интегральные символы?
Если вы хотите вставить интегральные символы в документы на базе Windows, используйте ярлыки альтернативного кода, указанные в столбце «Код Windows» в приведенной выше таблице. Например, alt + 10776 сделает интеграл со знаком времени как.
В документе Microsoft Word вы можете использовать шестнадцатеричный код, указанный в последнем столбце приведенной выше таблицы. Например, 2A19 Alt + X составит интеграл с символом пересечения, например ⨙.
Если у вас Mac, используйте «Код Mac», указанный в таблице выше. Например, option + 2A1C будет составлять интеграл с символом подчеркивания, например ⨜.
Примечание: Первый метод альтернативных кодов будет работать только с цифровой клавиатурой, поэтому вы можете использовать второй метод, используя обычные цифровые клавиши клавиатуры. Для третьего метода на Mac вам необходимо изменить метод ввода языка на Unicode Hex Input и переключить ввод из верхней панели меню.
Пример HTML-кода
Если вы хотите вставить интегральные символы в HTML, используйте один из форматов, приведенных в приведенном ниже примере кода. Обратите внимание, что только интегральный символ ∫ имеет имя объекта & int; и использовать десятичные и шестнадцатеричные коды для других символов в данном формате.
Пример кода CSS
Подобно HTML, вы также можете вставлять символы в CSS, используя шестнадцатеричный код. Ниже приведен пример кода, и вы можете использовать любое семейство шрифтов в коде.
Помните, как уже упоминалось, для математической документации вам следует использовать редактор формул или программное обеспечение, такое как LaTeX. В документах Office выберите «Вставить> Уравнение», чтобы открыть редактор формул. Щелкните раскрывающийся список «Интегральный», чтобы получить различные символы интеграла и создать уравнения.
Введите интегральные уравнения в Word