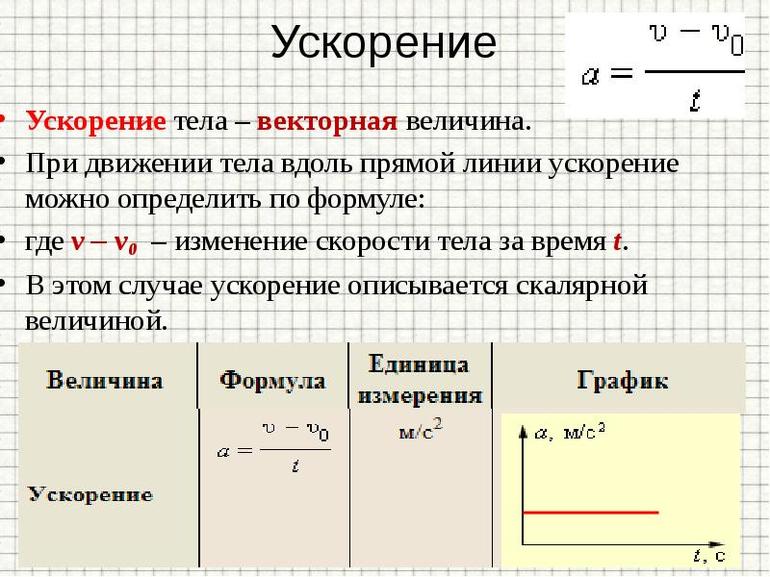
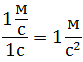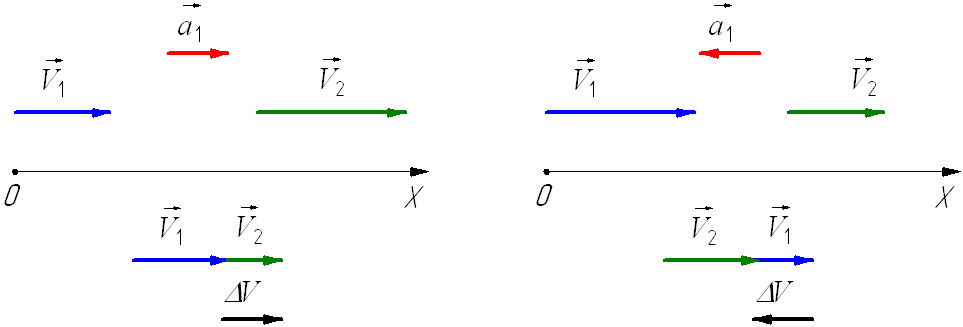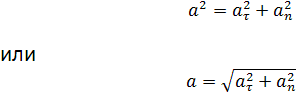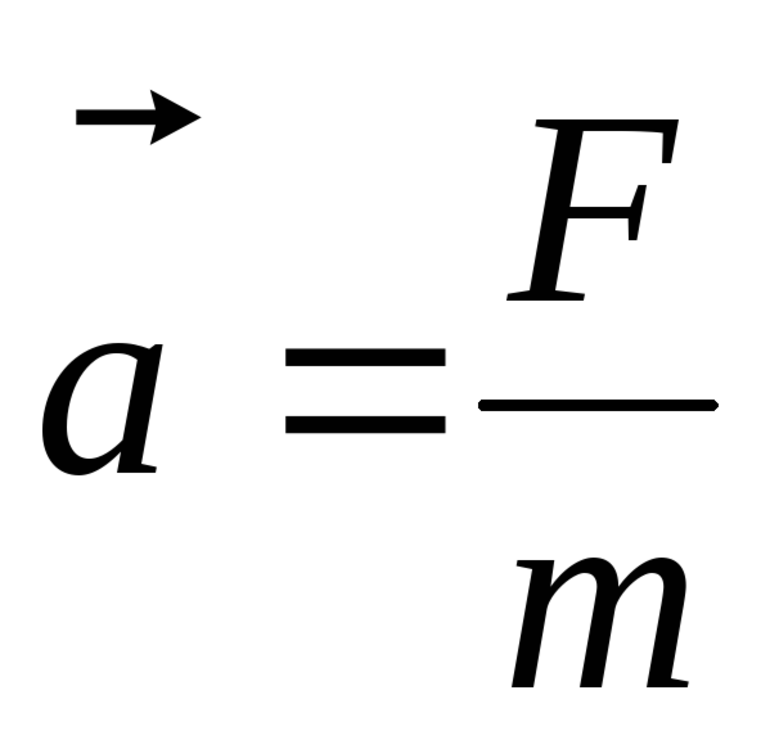Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи
В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.
Что такое ускорение?
Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:
Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.
Движение по прямой и ускорение
Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.
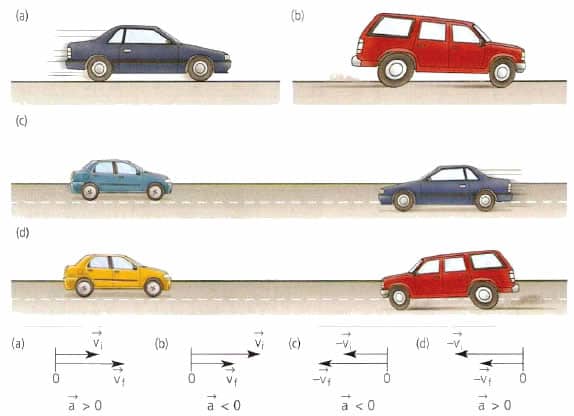
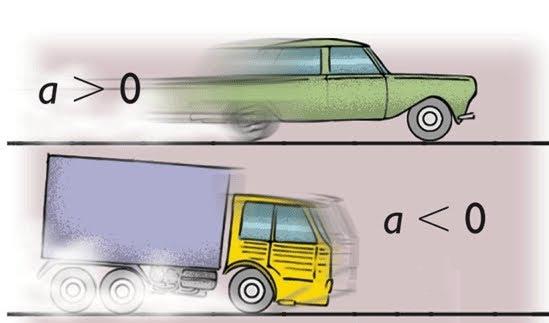
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).
Полное ускорение и его компоненты при движении тела по кривой
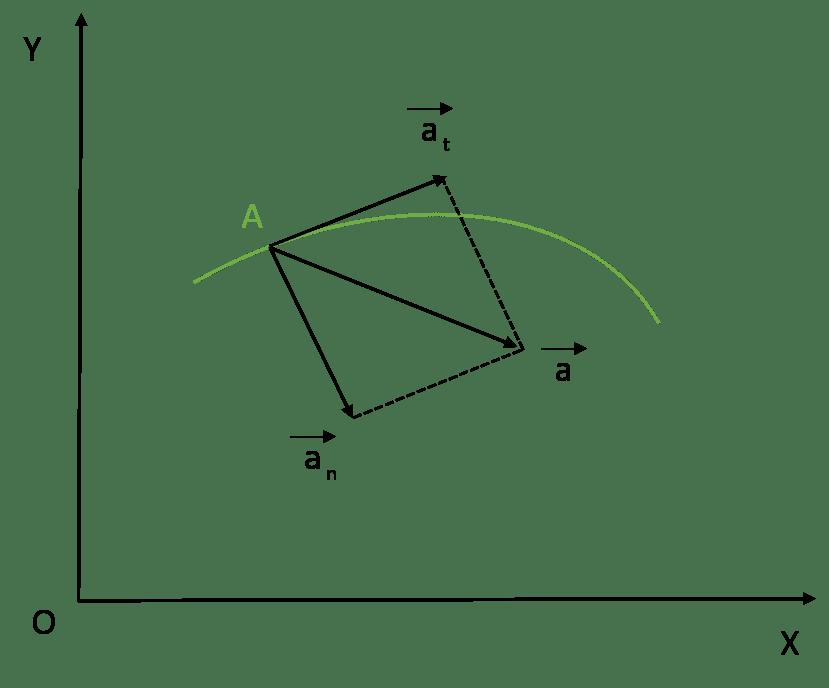
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:
Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:
Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.
Угловое ускорение
Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:
Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.
Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:
Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.
Пример решения задачи
Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:
Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.
Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:
at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.
Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).
Нормальная компонента вычисляется так:
an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.
Теперь можно рассчитать полное ускорение. Оно будет равно:
a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.
То есть, полное ускорение практически полностью образовано нормальной компонентой.
Наконец, ускорение угловое определяется по формуле:
α = at/r = 76/0,2 = 380 рад/с2.
Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
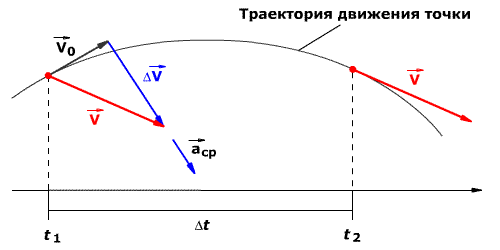
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 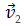
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
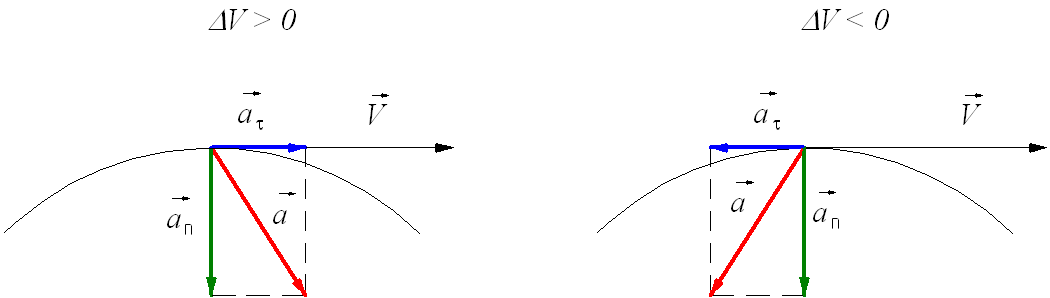
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 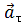
Нормальное ускорение
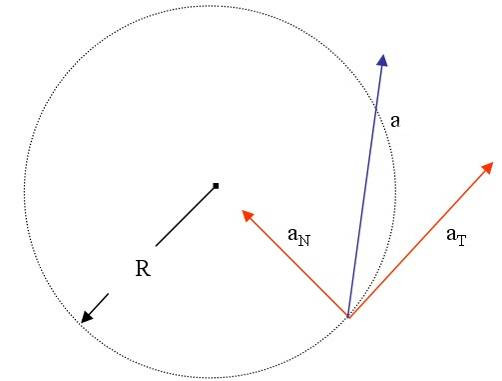
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 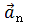
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Определение и свойства
Любое изменение скорости тела приводит к ускорению (ᾱ) как в сторону увеличения, что обычно подразумевается, так и снижения, то есть замедления. Также этот термин может означать смену направления (центростремительность). Это связано с прямой зависимостью сил, которые действуют на объект, от изменения скорости (v), являющейся величиной векторной и имеющей направление. Так ускоряться будут:
Например, транспортное средство начинает движение с места и продолжает ехать, увеличивая v, — это ᾱ линейное (или тангенциальное). Пассажиры внутри машины будут ощущать его как силу, которая прижимает их к спинкам сидений. Если автомобиль поворачивает, то есть меняет направление, то это уже ᾱ радиальное. Люди в салоне будут наклоняться в сторону, противоположную движению.
Когда водитель решит остановиться, это тоже будет ускорением, но только в противоположном направлении v движения авто. В космосе такое ᾱ называют ретроградным горением или замедлением. Пассажиры будут чувствовать, будто что-то их толкает вперёд. Принято различать два вида ᾱ:
Например, мотоцикл набирает скорость 50 м/с за 10 с, его среднее ᾱ = 50 / 10 = 5 м/с².
Другие формы
Можно взять материальный предмет, например, спутник, который вращается вокруг Земли. Он двигается по окружности и ускоряется, причина этого — изменение направления траектории движения. При этом его скоростной режим может не изменяться. В этом случае речь идёт о центростремительном (направленном к центру) ᾱ.
Ускорение тела относительно состояния свободного падения (ᾱ правильное) измеряется акселерометром. В механике для предмета с постоянной массой (m) ᾱ центра m тела пропорционально действующему на него вектору силы (суммы всех сил). Здесь действует второй закон Ньютона: F = m * ᾱ → ᾱ = F / m.
Скорость частицы, которая движется по криволинейной траектории, можно записать как функцию времени v(t) = v(t) * v(t) / v(t) = v(t) * ut(t), где единичный вектор касательной (ut) к траектории равен v(t) / v(t) и указывает направление движения в конкретный момент времени. Это и есть формула центростремительного ускорения, которое создаётся при круговом движении. Можно использовать цепное правило дифференцирования, чтобы записать формулу для произведения двух функций, если принять во внимание, что ᾱ частицы происходит по некой кривой проекции. Последовательность действий уравнения следующая:
В уравнении un — единичный вектор нормали, r — мгновенный радиус кривизны, который основывается на колеблющемся круге в момент времени t. Все эти компоненты являются тангенциальным, радиальным или нормальным ускорением, формула которого может быть представлена в виде функции.
Особые случаи
Если при движении v изменяется на равную величину, то есть объект равноускоренный в каждый одинаковый период времени, то это можно охарактеризовать как равномерное или постоянное ускорение. Пример этого в физике — формула ускорения свободного падения тела, вид которой при отсутствии сопротивления будет зависеть от гравитационного поля и силы стандартной гравитации (g).
Чтобы составить уравнение, придётся проделать небольшой путь от самых основ. Второй закон Ньютона гласит, что Fg = mg. В кинематике есть формулы, которые связывают смещение (sₒ), начальную (vₒ) и зависящую от времени v(t) скорость и ускорение с прошедшим временем (t):
Наглядно расчёт разности можно увидеть, если начертить график.
Частица будет испытывать ускорение, которое возникает в результате изменения направления вектора скорости, тогда как её величина остаётся постоянной при равномерном круговом движении. Производная от расположения точки на кривой по времени, то есть её v, оказывается всегда точно касательной к линии, соответствующей ортогональному радиусу в этой точке.
Это ускорение постоянно меняет направление скорости, которая будет касаться соседней точки, тем самым заставляя вектор скорости совершать вращательные движения по кругу. Формула будет выглядеть следующим образом: ᾱс = v² / r. Надо помнить, что v здесь — произведение угловой скорости ω на r.
Единица измерения
Ускорение рассчитывается путём деления метров в секунду (м/с) на секунды (с). Деление расстояния по времени вдвое равно делению расстояния на квадрат времени. Таким образом, единицей ускорения СИ является метр в секунду в квадрате (м/с²). Чтобы было весело изучать физику, можно рассмотреть несколько интересных примеров в таблице.
| ᾱ ( м/с²) | Событие |
| 0,5 | гидравлический лифт |
| 0,63 | ускорение свободного падения (УСП) на Плутоне |
| 1 | лифт на кабеле |
| 1,6 | ускорение свободного падения на Луне |
| 8,8 | Международная космическая станция |
| 10—40 | механический прямолинейный старт пилотируемой ракеты |
| 20 | космический челнок |
| 9,8 | УСП на Земле |
| 20—50 | американские горки |
| 80 | предел устойчивой человеческой терпимости |
| 0—150 | тренировочная центрифуга |
| 600 | автоматические подушки безопасности |
| 1 млн | пуля в стволе пистолета |
| 24,8 | УСП на Юпитере |
Другая часто используемая единица — ускорение силы тяжести g. Поскольку все знакомы с влиянием гравитации на физические объекты, это делает их удобным стандартом для сравнения ускорений. Все чувствуют себя нормально при 1 g, вдвое тяжелее при 2 g и невесомо при 0 g. Эта единица измерения имеет значение 9,80665 м/с², но для повседневного использования достаточно 9,8 м/с², а 10 м/с² удобно для быстрых подсчётов.
Действие на людей
Хотя термин «сила g» часто используется, g — мера ускорения, а не силы. Особую обеспокоенность у людей вызывают физиологические эффекты этого явления. Чтобы понять смысл, лучше обратиться к примерам:
По оценкам экспертов, ускорение во время аварии, в которой погибла принцесса Диана, составляло порядка 70—100 g.
Этого было достаточно, чтобы оторвать лёгочную артерию от её сердца и спровоцировать травму, которую практически невозможно пережить. Если бы Диана была пристёгнута ремнём безопасности, ускорение составило бы примерно 30 или 35 g. Это грозило несколькими переломами, но все остались бы живы.