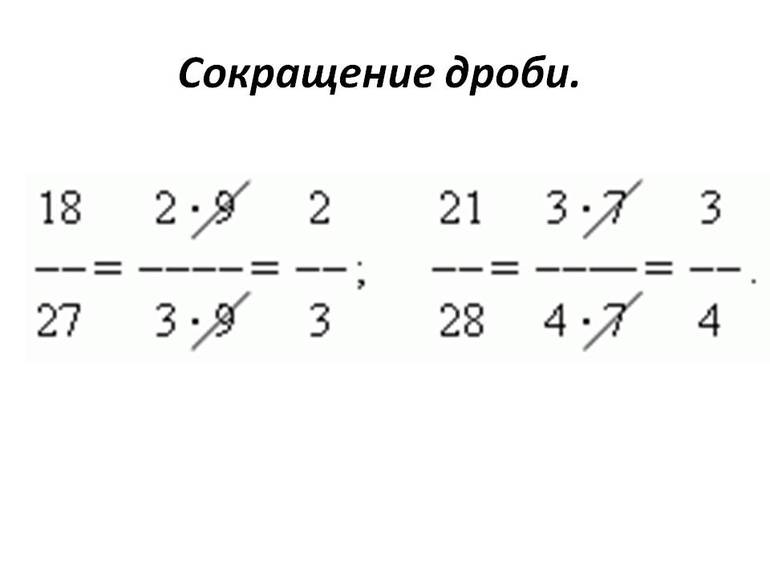
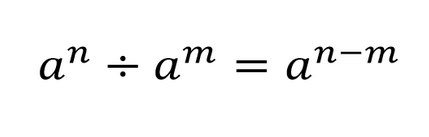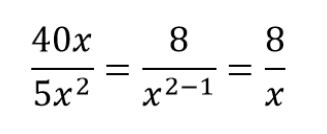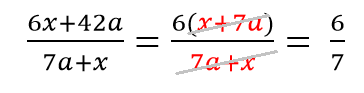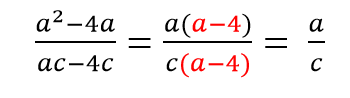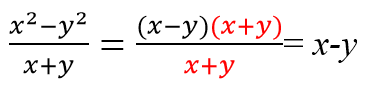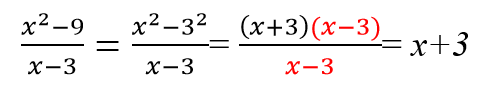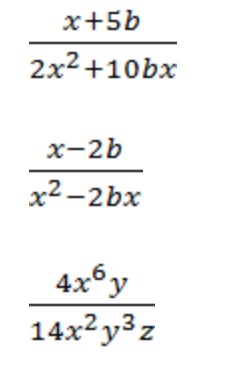Как сокращать дроби: простые примеры с подробными решениями
Содержание:
В этой статье коротко предоставим информацию о том, как сокращать дроби. Сначала приведем немного теоретической части, а затем подкрепим ее решением практических задач.
Что означает сократить дробь
Как сокращаются дроби
Как привести дробь к несократимому виду
Обычно алгебраическое решение любой задачи по сокращению дробей сводится к получению равной дроби, но в несокращаемом виде. Чтобы получить несократимую дробь, ее делят на определенное число, которое называется наибольший общий делитель (сокращенно НОД):
Практически рассмотрим, используя дробь \frac < 6 > < 12 >. Ее можно сократить на НОД, который равняется 6. Тогда 6 : 6 = 1 и 12 : 6 = 2. Следовательно:
Последняя дробь является несократимой.
Следует обратить внимание, что в большинстве случаев если требуется выполнить сокращение дробей, то это значит выполнить до получения несократимой дроби.
Как сократить большую дробь
В качестве нового примера возьмем дробь 144192. Сначала найдем наибольший общий делитель для чисел 144 и 192. Для этого можно применить метод разложения на простые множители:
144 : 2 = 72 192 : 2 = 96
72 : 2 = 36 96 : 2 = 48
36 : 2 = 18 48 : 2 = 24
18 : 2 = 9 24 : 2 = 12
Тогда наибольшим общим множителем для данных чисел будет число 48 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 2.
Разделив исходную дробь на 48 получим несократимую дробь:
Разберем еще один способ, который позволяет сокращать числитель и знаменатель дроби последовательно на делитель, который без труда определяется по простейшим математическим признакам. Если требуется сократить дробь типа 40008 800, то можно сразу же определить, что здесь присутствует общий множитель 100, который можно вынести за скобку:
Далее невооруженным глазом заметно, что оба числа делятся на 2, а результат опять на 2 и т. д. В конечном итоге получаем несократимую дробь \frac < 5 > < 11 >= \frac < 4000 > < 8800 >. Теперь можно сказать, что наибольшим общим делителем для данной дроби было число 800.
В заключении заметим, что если знаменатель дроби представляет собой числитель, возведенный в квадрат, то такая дробь в несокращаемом виде всегда будет представлять собой: 1 – в числителе + число, значившееся числителем до сокращения, в знаменателе:
Сокращение дробей: правила и примеры
Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.
Что такое «сокращение дробей»
В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.
Приведение дробей к несократимому виду
Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.
Приведение дроби к несократимому виду
Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.
6 24 = 6 ÷ 6 24 ÷ 6 = 1 4
Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.
Правило сокращения дробей
Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.
Правило сокращения дробей
Чтобы сократить дробь нужно:
Рассмотрим практические примеры.
Пример 1. Сократим дробь.
Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.
182 195 = 182 ÷ 13 195 ÷ 13 = 14 15
Готово. Мы получили несократимую дробь, которая равна исходной дроби.
Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.
Пример 2. Сократим дробь
Для этого представим исходную дробь в виде:
360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7
Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:
360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7 = 2 · 3 7 · 7 = 6 49
Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.
Пример 3. Сократим дробь
2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44
20 44 = 20 ÷ 2 44 ÷ 2 = 10 22
Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:
Общие сведения
Первые упоминания о дробях встречаются в Древнем Египте. Его жители умели делить два предмета на три части. Применяли они для этого специальное обозначение: 1/2, 2/3, 1/3. При этом запись вида 2/3 была единственной, где в верхней части использовалась не единица, а двойка. Египтяне для обозначения, впрочем, как и вавилоняне, использовали формулу: 1/ n. Для записи других дробей использовалась сумма. Например, вместо 8/15 они использовали сложение двух выражений: 1/3 и 1/5.
Работать с такими дробями было сложно. Различные философы и учёные пытались придумать запись, универсальную для любых случаев. Так, были попытки использовать шестидесятеричные дроби, которыми пользовались в Вавилоне и Греции. Но выполнять над ними операции опять же было сложно. В Риме использовали систему, называемую асс. В её основе лежало деление на двенадцать. Долю, которую она составляла, называли унцией.
Современную же систему записи предложили в Индии. Единственным отличием от общепринятой записи была её перевернутость. Сверху писали делимое, а внизу — делитель. Дробную черту не ставили. Запись же, используемая сегодня, была предложена арабами.
Любая дробь состоит из двух частей: верхней, называемой числителем, и нижней — знаменателя. При произношении читается сначала числитель, а после знаменатель. Например, 3/8 — три восьмых. Верхняя часть обозначает, сколько взято долей, а нижняя — каких. В алгебре используется и иная формулировка. Числитель называют делимым, а знаменатель делителем.
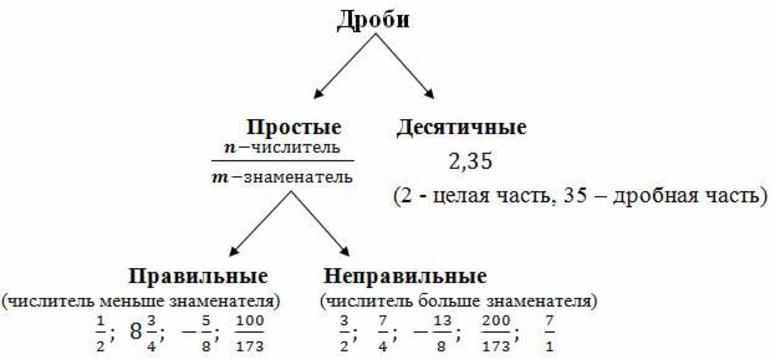
Существуют следующие виды дробей:
В любом виде отношений могут стоять определённые числа или неизвестные переменные. Поэтому сократить дробь можно как со степенями, так и буквами или цифрами. На правило упрощения содержание делителя и делимого не влияет.
Свойства дроби
По сути, сократить дробь — значит, её упростить. Можно использовать разный алгоритм, но в любом случае применяется основное свойство отношений. Заключается оно в том, что если делитель или делимое умножить на одно и то же число, то количественное значение в ответе не изменится. Это правило справедливо и при замене операции умножения на деление.
Алгебраически свойство можно записать в виде равенства: (q * c) / (r * c) = q / r. Для объяснения этого правила используется следующее доказательство. Пусть имеется равенство (q * r) * c = (c * r) * q. Оно возможно, так как соответствует закону умножения натуральных чисел. При этом учитывается свойство деления, согласно которому, если число разделить на равное ему значение, то результатом действия будет единица. Например, с / с = 1 или 12к/12k = 1. Последнее правило довольно логичное и интуитивно понятное. Если представить, что есть число вещей, равное x, и их нужно разложить на кучки так, чтобы в каждой оказалось x предметов, то очевидно, что получится лишь одна кучка.
Исходя из этих двух правил, можно утверждать, что выражения q * c / r * c и q : c / r : c равны q / r. То есть эти два выражения равны друг другу. На уроках математики в школе предлагают графическую иллюстрацию основного свойства. Пусть есть квадрат, который набран из девяти других квадратов. Каждый из них, в свою очередь, разделён на четыре части. Можно утверждать, что основная фигура поделена на 9 * 4 = 36 частей.
Если закрасить пять больших квадратов другим цветом, то фактически будет окрашено 20 квадратов меньшего размера (4 * 5). Отмеченная область составляет 5/9 от целого квадрата или 20/36, если считать маленькие фигуры. Но так как окрашенная часть одна, то справедливо будет утверждать о верности равенства 5 / 9 = 20 / 36. Вместо чисел 20 и 36 можно подставить их произведения. В итоге получится выражение: 5 / 9 = 5 * 4 / 9 * 4 = 20 * 4 / 36 * 4 = 20 / 36. Что и следовало доказать.
Свойство дроби используется при поиске наименьшего и наибольшего общего знаменателя, а также позволяет упрощать выражения. Невозможно правильно научиться сокращать дроби, не понимая рассмотренного правила.
Алгоритм сокращения
Существующие дроби можно разделить на сократимые и несократимые. Сократить отношение — значит, разделить верхнюю и нижнюю часть на общий делитель. При этом его значение не должно быть равное единице. В итоге получится новое выражение с меньшим значением делителя и делимого. Например, пусть дана дробь 16 / 24. Числитель и знаменатель выражения можно разделить на восемь. В результате запись упростится до вида 16:8 / 24:8 = 2 / 3. Полученная дробь является уже несократимой и её дальнейшее упрощение невозможно.
Любое упрощение выражения можно представить в виде следующего алгоритма:
Таким образом, суть действия сводится к нахождению такого сократителя, после применения которого она превратится в тождественную начальной, но уже станет несократимой. Наибольшим общим делителем (НОД) называют одночлен или многочлен, являющийся самым большим из всевозможных делителей, на которое числитель и знаменатель делится без остатка. Например, для чисел 12a и 24a НОД будет равный 12a.
Чтобы быстро найти НОД, нужно знать таблицу умножения и уметь раскладывать числа на простые множители. Ими называют числа, которые делятся на единицу и сами на себя. Существует даже таблица простых чисел до 997, с которой знакомят на уроках алгебры в 7 классе. Но многие натуральные числовые выражения могут делиться и на другие цифры без остатка. Например, двенадцать можно разделить на 1, 2, 3, 4, 6, и 12. Эти числа называют делителями.
При разложении используется запись в виде столбика с вертикальной чертой. В правой части пишут делимое, а в левой — исходное значение. Начинают пробовать делить на двойку, если действие невозможно, повышают значение делимого на единицу. Например, 45 = 3 * 3 * 5.
При поиске НОД каждый знаменатель раскладывают на простые множители, а затем находят одинаковые цифры и перемножают их. Полученный ответ и будет искомым сокращателем. Например, в числителе стоит число 24, а в знаменателе 42. Согласно правилу, их нужно разложить: 24 = 2 * 2 * 2 * 3 и 42 = 2 * 3 * 7. В одной и другой записи повторяются цифры три и два. Их произведение 2 * 3 = 6 и является НОД, на который и будет сокращаться дробное выражение. То есть 24:6 / 42:6 = 4 / 7. Полученная дробь является уже несократимой.
Сложные выражения
Многочлены, стоящие в числителе или знаменателе, имеющие первую степень, сокращать довольно легко. Но часто в задании попадаются степенные выражения. Для того чтобы их упростить, нужно хорошо знать основные формулы и свойства степеней. Заключаются они в следующем:
В заданиях могут встречаться рациональные и простые числа, известные и неизвестные. Решают их таким же образом. Например, нужно сократить дробь со степенями и буквами: ((0,25 ) p +1 * 8 p ) / (2 2p+1 * (0,5) p-1 ) = (0,25 p * 0,25 1 * 8 p ) / (2 2p * 2 1 * 0,5 p :0,5 1 ) = (1 / 4) p * 0,25 * 8 k / 4 p * 4 * 0,5 p = 2 p * 0,25 / 2 p * 4 = 0,25 / 4 = (1/4) / 4 = 1 / 4* 4 = 1/16.
Смотря на этот пример, можно понять важность упрощения дробей. Ведь из задания, практически недоступного для решения, получилось простейшее наглядное выражение. Но при этом может случиться так, что исходная формула будет довольно сложна для предварительного анализа, например, содержать квадратный корень, экспоненту или логарифм. Для таких случаев есть резон использовать специализированные сайты-вычислители.
Использование онлайн-калькулятора
Воспользоваться возможностью сократить дробь на онлайн-калькуляторе сможет любой пользователь интернета. Такую услугу бесплатно предоставляют несколько десятков специализированных сайтов. Неоспоримое их преимущество заключается в быстром и правильном упрощении любого дробного выражения. При этом от пользователя не требуется никаких математических знаний.
Всё что необходимо, это подключение к сети и веб-браузер с поддержкой Flash плеера. Пользователю нужно просто зайти на сайт и в предложенную форму ввести упрощаемую формулу, а затем нажать виртуальную кнопку «Рассчитать». Программа сделает все вычисления самостоятельно, используя оптимальный алгоритм.
Кроме того, на этих сайтах содержится теоретический материал. Он часто подкреплён примерами. Причём даётся не просто ответ, а приводится вся цепочка вычислений, по которой можно разобраться в сути действий.
Из доступных сайтов можно выделить несколько, наиболее популярных среди пользователей:
Применение онлайн-калькуляторов может стать частью учебного процесса. Учащийся, вводя различные дроби, может воочию видеть нюансы сокращения того или иного вида выражений, а также использовать ресурсы для проверки самостоятельного решения.
Сокращение алгебраических дробей: правило, примеры.
Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.
Смысл сокращения алгебраической дроби
В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.
Сокращение алгебраической дроби представляет собой аналогичное действие.
Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.
Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.
Все ли алгебраические дроби подлежат сокращению?
С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.
Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.
Правило сокращения алгебраических дробей
Правило сокращения алгебраических дробей состоит из двух последовательных действий:
Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.
Характерные примеры
Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:
Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).
К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105
Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:
(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:
24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105
По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.
Решение
Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:
Однако, более рациональным способом будет запись решения в виде выражения со степенями:
Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).
Решение
Возможно сократить дробь таким образом:
Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.
Решение
Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:
Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:
Краткое решение без пояснений запишем как цепочку равенств:
Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.
Решение
На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:
Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:
Теперь становится виден общий множитель, осуществляем сокращение:
Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.
Как сокращать алгебраические дроби?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
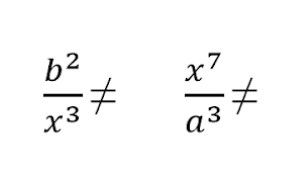 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
Примеры сокращения дробей с помощью формул сокращенного умножения:
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.