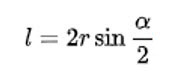Хорда (геометрия)
Хорда в планиметрии — отрезок прямой линии, соединяющей две точки данной кривой (например, окружности, эллипса, параболы).
Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегмент.
Хорда, проходящая через центр окружности, называется диаметр. Диаметр — это самая длинная хорда в окружности.
Содержание
Свойства хорд
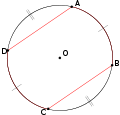
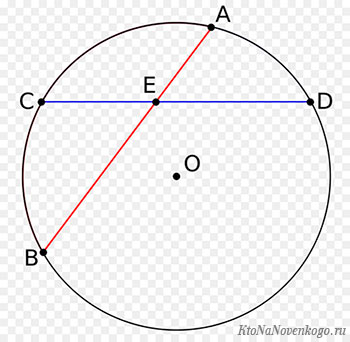
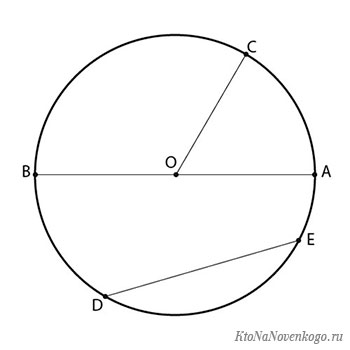
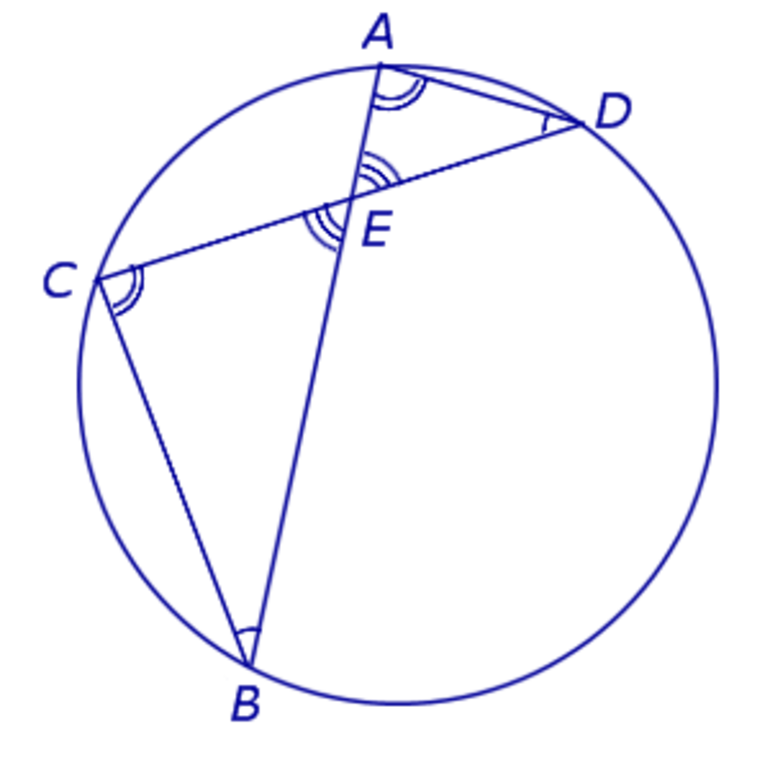
Дуга AB равна дуге CD. Дуга BC равна дуге DA
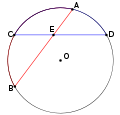
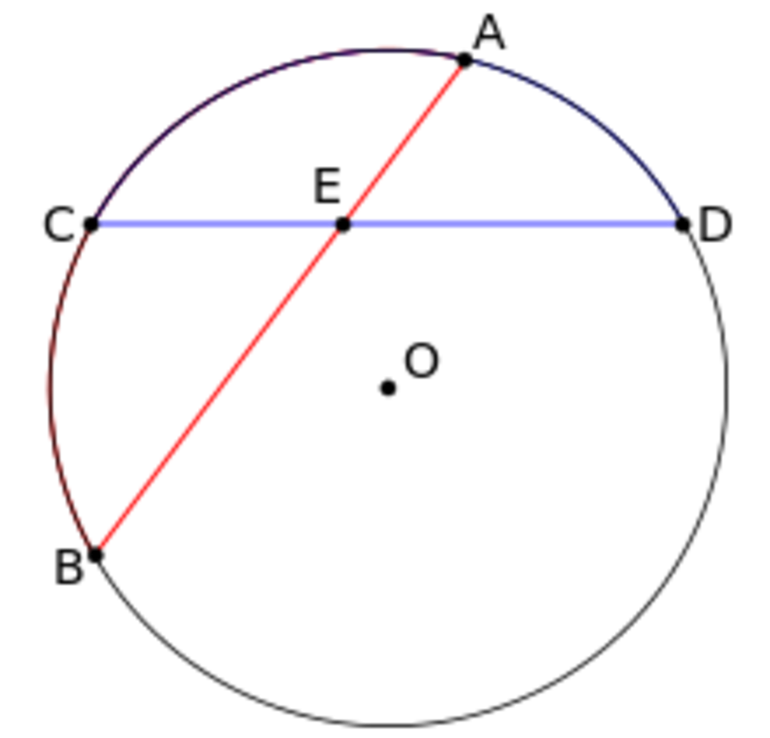
Произведение отрезков одной хорды равно произведению отрезков другой хорды: AE×EB = CE×ED
Основные формулы
Связанные понятия и утверждения
Ссылки
Полезное
Смотреть что такое «Хорда (геометрия)» в других словарях:
Геометрия Лобачевского — (1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Геометрия Лобачевского (гип … Википедия
Хорда окружности — Окружность и её центр Окружность геометрическое место точек плоскости, равноудаленных от заданной точки, называемой её центром. В Викисловаре есть статья «окружность» Вписанная окружность Описанная окружность Окружность Аполлония Единичная… … Википедия
Лобачевского геометрия — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
Начертательная геометрия — Начертательная геометрия инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов. Практически, начертательная геометрия ограничивается исследованием объектов … Википедия
Начертательная геометрия* — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Начертательная геометрия — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
История тригонометрии — Геодезические измерения (XVII век) … Википедия
Диаметр — в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам. Содержание 1 Диаметр геометрических фигур … Википедия
Кривая второго порядка — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида в котором по крайней мере один из коэффициентов отличен от нуля. Содержание 1 История 2 … Википедия
Хорда — это геометрическая струна
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы подробно расскажем, что такое ХОРДА.
Слово это имеет древнегреческие корни и переводится как «струна».
Это очень точно характеризует ее внешний вид, так как хорда представляет собой прямую линию.
Хорда — это.
Термин ХОРДА применяется сразу в нескольких областях:
В геометрии хорда – это часть прямой, которая проходит между двумя точками на окружности или эллипсе;
Но в рамках этой статьи мы подробно рассмотрим первый вариант значения термина ХОРДА. Тот, который применяют в геометрии, и который школьники подробно изучают в 7 классе.
Что такое хорда в геометрии
Хорда – это отрезок прямой, которая проходит через две точки на любой кривой линии. Это могут быть окружность, эллипс, гипербола или парабола.
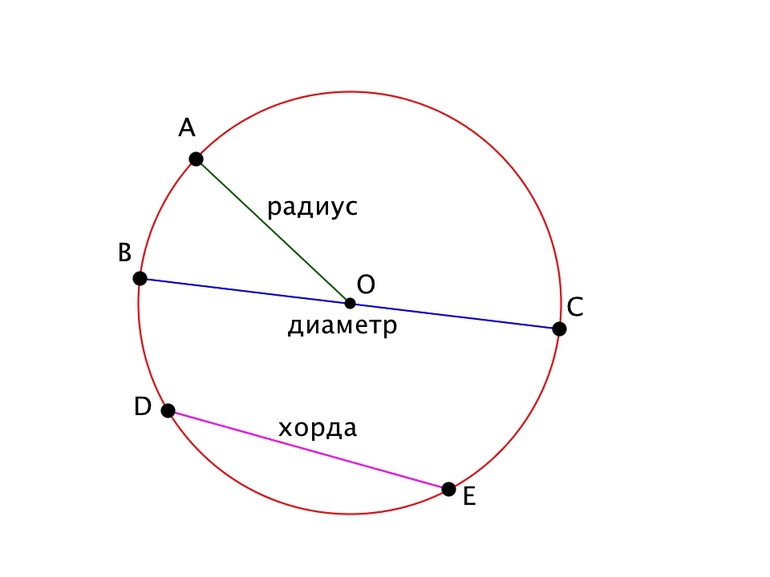
Выглядит хорда вот так:
На этом рисунке изображены сразу две хорды – AB и CD. А есть еще частный случай, когда хорда проходит через центр окружности.
Такая хорда, на данном рисунке это отрезок AB, будет являться диаметром окружности. И как нетрудно догадаться, это самая длинная хорда, которая может быть для данного примера.
Свойства хорды
Если сравнивать хорду с другими частями окружности, то можно вывести целый ряд закономерностей.
Например, хорда и радиус:
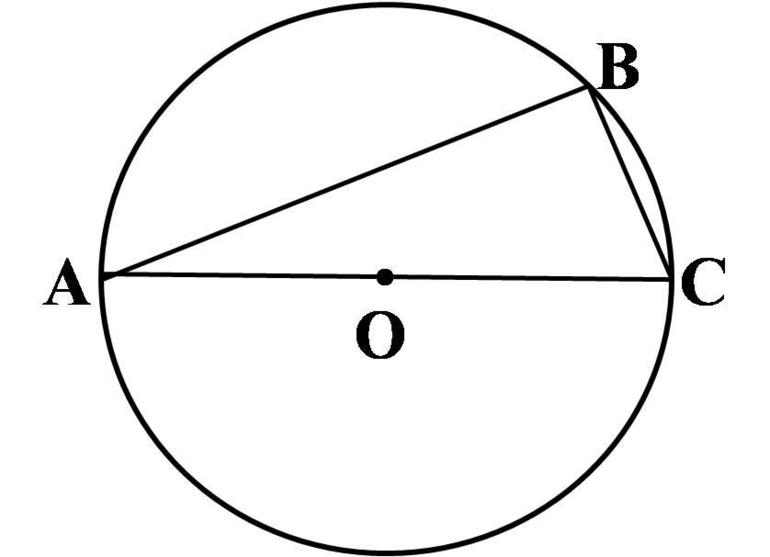
Хорда и диаметр:
Хорда и центр окружности:
И еще одно свойство хорд в окружности. Если взять уже знакомый нам рисунок расположенный сразу под определением, то при пересечении хорд получается вот такая зависимость – произведение частей одной хорды равна произведению частей другой:
Как рассчитать длину хорды
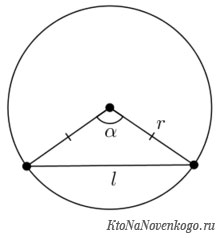
Длина хорды – это расстояние от одной точки пересечения с окружностью до другой. Чаще всего она обозначается латинской буквой «L».
Чтобы рассчитать длину хорды, надо знать значение радиуса и центрального угла. Формула выглядит так:
Вот и все, что мы хотели рассказать о ХОРДЕ.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Не знаю, что делать школьникам с этими знаниями, вот мне эти хорды нигде не пригодились, далеко не всю геометрию можно направить в практическое русло.
Хорда в геометрии
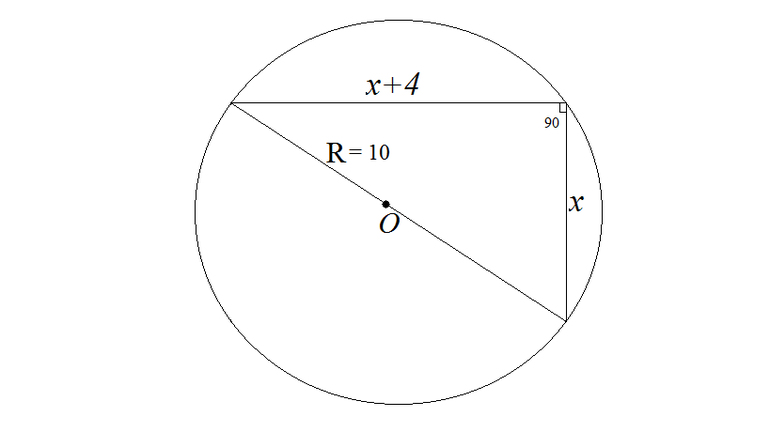
Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.
Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.
Свойства отрезка окружности
Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.
Ключевая теорема
Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.
Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.
Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.
Касательная и секущая
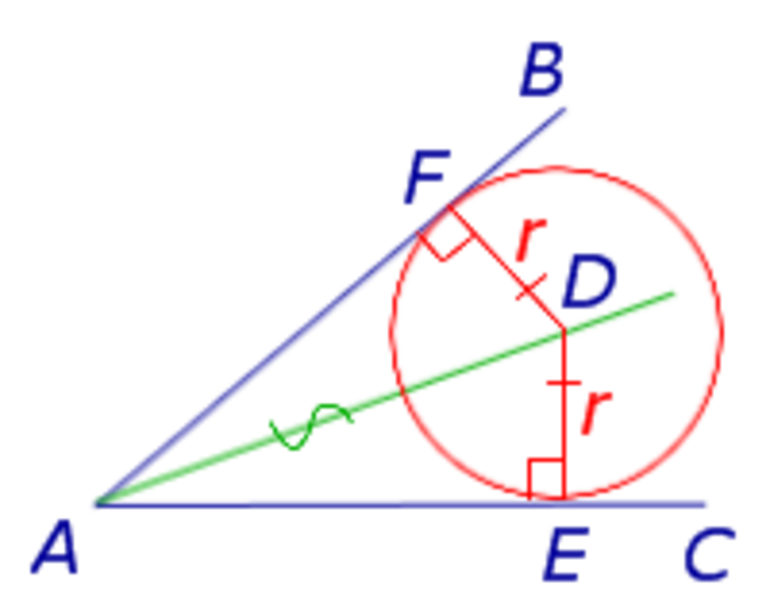
Существует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.
Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
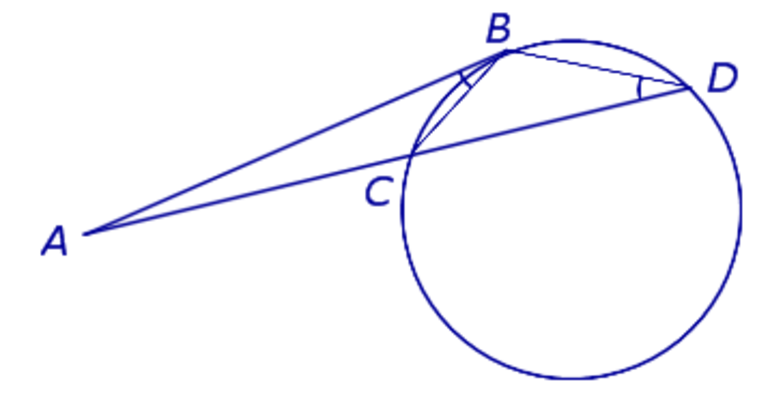
Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
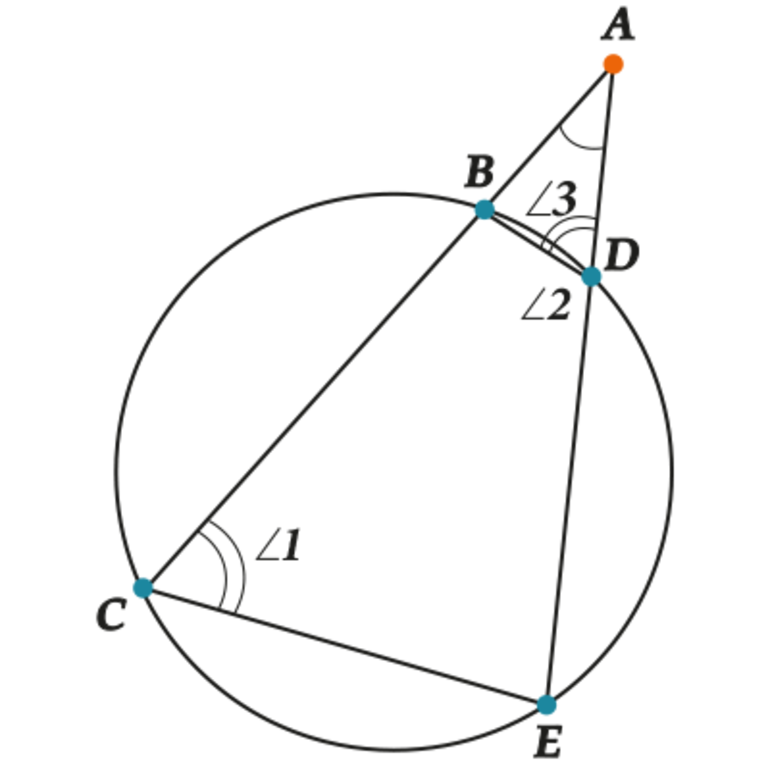
Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.
Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.
Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.
Решение задач
При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.
Окружность
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
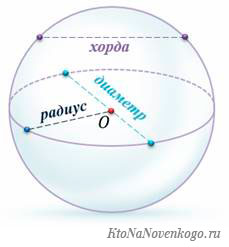
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ 
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги 

Хорда окружности
Окружность — геометрическое место точек плоскости, равноудаленных от заданной точки, называемой её центром.
В Викисловаре есть статья « окружность » Литература | |
| Неплоские кривые | |
|---|---|
| Винтовая линия • Линия откоса • Локсодрома • Ортодромия • Губка | |
| Связанные понятия | |
| Определения кривой | Аналитическая кривая • Кривая Жордана • Канторова кривая • Кривая Урысона |
| Преобразованные кривые | Эволюта • Эвольвента • Каустика |
| Конические сечения | |
|---|---|
| Главные типы | Эллипс • Гипербола • Парабола |
| Вырожденные | Точка • Прямая • Пара прямых |
| Частный случай эллипса | Окружность |
| Геометрическое построение | Коническое сечение • Шары Данделена |
| Математика • Геометрия | |
Полезное
Смотреть что такое «Хорда окружности» в других словарях:
Хорда — В Викисловаре есть статья «хорда» Хорда: Хорда окружности в планиметрии отрезок прямой линии, соединяющей две точки данной кривой (круг … Википедия
ХОРДА — (греч. chorde). В геометрии: прямая линия, соединяющая концы дуги. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ХОРДА 1) в геометрии прямая линия, соединяющая две какие нибудь точки окружности, но не проходящая… … Словарь иностранных слов русского языка
ХОРДА — ХОРДА, хорды, жен. (греч. chorde струна). 1. Прямая, соединяющая две точки какой н кривой линии, напр. концы дуги окружности (мат.). 2. Осевой скелет, упругий эластичный тяж, спинная струна (лат. chorda dorsalis у некоторых животных (напр. рыб, т … Толковый словарь Ушакова
ХОРДА 1 — ХОРДА 1, ы, ж. В математике: прямая, соединяющая две точки кривой, напр. дуги, окружности. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
хорда — ХОРДА, ы, жен. В математике: прямая, соединяющая две точки кривой, напр. дуги, окружности. II. ХОРДА, ы, жен. (спец.). Спинная струна первичная скелетная ось у высших животных и человека. | прил. хордовый, ая, ое. Тип хордовых (сущ.; тип высших… … Толковый словарь Ожегова
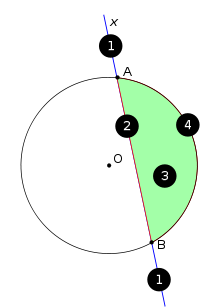
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
ХОРДА — (от греч. chorde струна) отрезок прямой, соединяющий 2 точки к. л. кривой линии, например окружности … Большой энциклопедический политехнический словарь
Фокальная хорда — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия
Парадокс Бертрана (вероятность) — Для термина «Парадокс Бертрана» см. другие значения. Парадокс Бертрана проблема классического определения теории вероятностей. Жозеф Бертран описал парадокс в своей работе Calcul des probabilités (1888) в качестве примера того, что вероятность не … Википедия
ГОСТ 16531-83: Передачи зубчатые цилиндрические. Термины, определения и обозначения — Терминология ГОСТ 16531 83: Передачи зубчатые цилиндрические. Термины, определения и обозначения оригинал документа: 5.3.1. Воспринимаемое смещение Разность межосевого расстояния цилиндрической зубчатой передачи со смещением и ее делительного… … Словарь-справочник терминов нормативно-технической документации