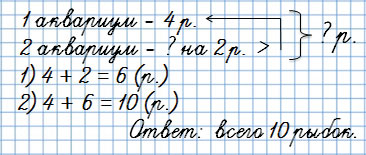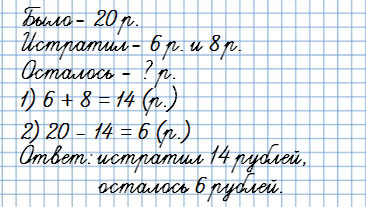Написать задачу и получить решение по математике
Математика – царица наук. Её язык одинаков во всех странах и континентах, и образование ребёнка начинается, прежде всего, с изучения языка и математики. Математика в тех или иных формах изучается во всех классах общеобразовательной школы, способствуя повышению умственных способностей и развитию математических навыков ученика. Учебный процесс непосредственно связан с решением различных математических задач, которые задаются ученикам как на уроках, так и в форме домашних заданий. Если вы столкнулись с трудностями в их решении, вам помогут специальные сетевые сервисы и мобильные приложения, позволяющие решить задачу по математическим дисциплинам. Ниже мы разберём их перечень, а также поясним, как ими пользоваться.
Math10 – универсальный сетевой ресурс для решения задач
Сервис math10.com – универсальный сетевой ресурс для решения математических задач. Сервис позволяет решать задачи и примеры по базовой математики, алгебре, тригонометрии, статистике, линейной алгебре, химии и других точных науках. Ресурс является одним из лучших в данном плане, и может быть рекомендован всем желающим быстро решить ту или иную задачу онлайн.
Для работы с ресурсом выполните следующее:
Mateshka – поможет решить задачу с картинками
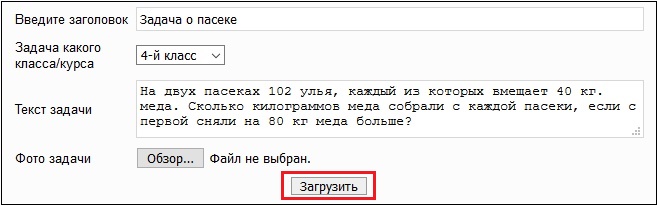
Сервис mateshka.ru представляет собой довольно универсальный решебник, позволяющий решать различные виды задач. Его функционал позволяет работать не только с отдельными примерами в полуавтоматическом режиме (как в случае предыдущего сервиса), но и загружать сфотографированные картинки с условием задачи, и получить через какое-то время готовый результат.
Для работы с сервисом выполните следующее:
- Введите условие задачи в соответствующую форму, а затем нажмите на «Загрузить»
Math-solution — помощь в решении математики онлайн
Ресурс math-solution.ru пригодится учащимся, которые в том или ином объёме изучают математику и геометрию, и поможет в решении соответствующих задач. В основу сайта положены математические программы (калькуляторы) для решения задач онлайн. Все необходимые вычисления выполняются на сайте, представлен поэтапный вариант получения ответа.
Для работы с сервисом выполните следующее:
Math.semestr.ru – онлайн-калькулятор
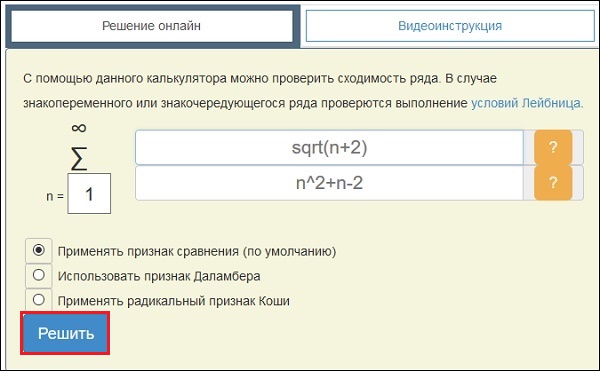
Сервис https://math.semestr.ru/example.php представляет собой различные калькуляторы по направлениям, включая высшую математику, аналитическую геометрию, вычислительную математику, статистику и другие дисциплины. Для решения имеющейся у вас задачи перейдите на данный ресурс, выберите интересующий вас калькулятор, тип задачи, вбейте данные, и нажмите на «Решить».
Кontrolnaya-rabota.ru – решение математических задач онлайн
Еще одним ресурсом для решения математических задач является kontrolnaya-rabota.ru, позволяющее ввести автоматическое уравнение и получить его автоматическое решение. Интерфейс сервиса очень прост и интуитивно понятен, позволяя быстро получить нужный результат. Выполните следующее:
Webmath.com – англоязычный ресурс для решения математических задач
Англоязычной альтернативой для решения различных типов математических задач является сервис webmath.com. Данный сайт генерирует ответы на определённые математические вопросы и задачи, вводимые пользователем. Ответы генерируются и отображаются в реальном времени. Помимо ответов, сервис показывает учащимся, как пройти к тому или иному ответу.
Для работы с сервисом выполните следующее:
Quickmath.com – решить математическую задачу быстро онлайн
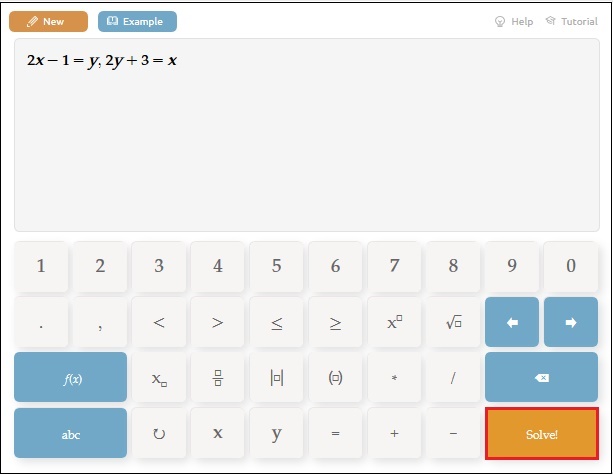
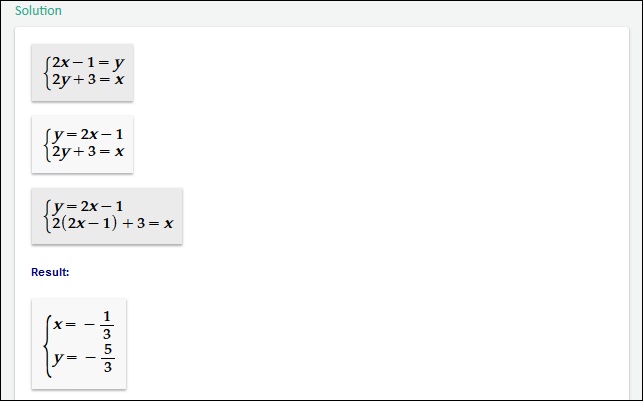
Альтернативным англоязычным ресурсом для поиска решения задач по математике является quickmath.com. Его функционал также позволяет в автоматическом режиме решать различные виды математических задач. Работа с ним не отличается от сервисов-аналогов. Перейдите на ресурс, введите в специальное поле задачу для решения, и нажмите внизу на «Solve».
Через несколько секунд вы получите результат с вариантами ответа.
Мобильные приложения для решения математических задач
Также отметим ряд специализированных математических приложений, позволяющих с помощью вашего телефона решить ту или иную задачу. Они следующие:
Заключение
В статье рассмотрены сетевые сервисы и мобильные приложения, позволяющие написать условие задачи по математике и довольно быстро получить её решение. Каждый из перечисленных нами инструментов может оказаться полезным в решении вашей задачи, поскольку не только предоставляет конечное решение, но подробно описывает промежуточные шаги. Столкнувшись с трудной задачей, используйте данные сервисы и приложения, которые позволят вам быстро справиться с заданием, получив высокий оценочный бал.
Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
Сколько грибов нашёл Володя?
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было. Стало. «
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было. Осталось. «
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали. Осталось. «
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Сколько рыбок в двух аквариумах?
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
Задачи с составлением рисунка по условию:
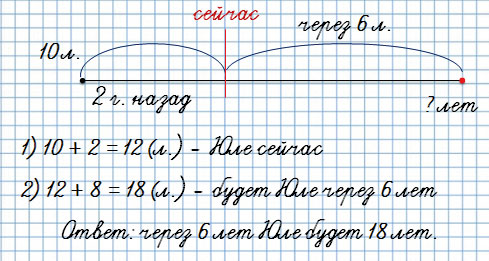
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Поделись с друзьями в социальных сетях:
Как решить любую задачу? Часть 1. Алгебра

Придумывать новое решение самостоятельно – это тоже навык, который надо развивать. Нужно привыкнуть не бояться нового, уметь задавать себе правильные вопросы и лояльно относиться к своим ошибкам. В этой статье я написала, что помогает лично мне и моим ученикам решать новые задачи.
Предупреждаю: это всё работает только если вы знаете необходимую теорию. То есть уметь отличать рубанок от ножовки всё-таки надо. 🙂
5 принципов которые помогут решить задачу:

Если закрыта одна дверь, открыта другая. Не циклись на одной мысли. Возможно, к решению можно подойти вообще с другой стороны. Но перед тем как зачеркивать очередную попытку решения – внимательно проверь, может быть ты просто сделал в нем какую-то простенькую ошибку и поэтому не получается дорешать до конца?
8 вопросов, которые помогут решить почти любое задание в алгебре
Решая задачу, мы ищем ответ на вопрос задания – нужное значение переменной, интервал решений или еще что-то в этом роде. И чтобы прийти к ответу на этот главный вопрос нужно уметь задавать себе промежуточные, опорные вопросы, которые могут натолкнуть на правильный путь рассуждений. Вот эти вопросы:
1. Что передо мной (уравнение, неравенство, выражение)? Как обычно решается такой тип задач?
— Что передо мной?
— Квадратное неравенство.
— Как решаются квадратные неравенства?
— Методом интервалов.

\(x∈[-10;10]\)
Пример 2: Решите уравнение \(\cos\) \(\frac<π(x-7)><3>\) \(=\) \(\frac<1><2>\)
— Что передо мной?
— Простейшее тригонометрическое уравнение.

\(\frac<π(x-7)><3>\) \(=±\) \(\frac<π><3>\) \(+2πn,n∈Z\)
— А теперь что передо мной?
— Хм… Выглядит странно, но похоже на линейное уравнение, так как тут только одна переменная (\(x\)) и она в первой степени.
— Как решаются линейные уравнения?
— Нужно избавиться от знаменателей, раскрыть все скобки и перенести известные вправо, а неизвестные влево, в общем, привести уравнение к виду \(x=[число]\).
2. Решал ли я похожие задачи? Как я их решал?
— Что передо мной?
— Тригонометрическое уравнение (не простейшее).
— Как обычно решаются тригонометрические уравнения?
— Уравнение преобразовывается с помощью формул, пока невозможно будет сделать замену. Очевидно, что тут сразу можно сделать замену.
Получилось кубическое уравнение.
— Решал ли я похожие задачи? Как я их решал?
— Обычно кубические уравнения я решал либо методом группировки, либо делением многочлена на многочлен.
3. Какие формулы я вижу / какие формулы можно применить? Что надо сделать, чтоб их можно было применить?
— Какие формулы я тут вижу?
— Полностью – никаких. Но вот такое же произведение синус на косинус есть в формуле двойного угла синуса:
4. Какие «неслучайности» я вижу? Как их можно использовать?
— Какие «неслучайности» я вижу?
— Очевидно, что выражения \((4x-8)\) и \((x-8)\) с той и другой стороны – это неспроста.
— Как их можно использовать?
— Поделить на эти выражения нельзя. Можно попробовать перенести то, что стоит справа в левую часть.
Теперь можно одинаковые выражения вынести за скобку.
— Какие «не случайности» можно заметить?
— И \(9\), и \(27\) являются степенями тройки: \(3^2=9\), \(3^3=27\).
— Как это можно использовать?
— Можно заменить \(9\) на \(3^2\), а \(27\) на\( 3^3\), вот так:
А теперь можно применить свойство степеней: \((a^n)^m=a^
5. Что я в принципе могу сделать? Какие преобразования допустимы/возможны?
— Что можно сделать с этим выражением?
— Можно вынести множители из-под знака корня.
— Какие еще преобразования здесь возможны?
— Можно вынести за скобки \(4\sqrt<2>\).
— Что еще можно сделать?
— Применить формулу двойного угла \(\cos2α=1-2\sin^2α \)
6. Что мне мешает? Как можно сделать выражение/уравнение/неравенство проще? Как мне было бы удобнее? Что я могу сделать, чтоб стало удобнее?
— Как можно сделать уравнение сильно проще?
— Если избавиться от корня, то уравнение станет проще.
— Как можно избавиться от корня?
— Можно возвести обе части уравнения в квадрат.
— Как можно упростить уравнение?
— Можно избавиться от знаменателя.
— Как обычно избавляются от знаменателя?
— Умножением обеих частей уравнения на наименьший общий знаменатель.
— Как было бы удобнее?
— Было бы удобнее, чтоб аргументы у логарифмов были одинаковые.
— Что надо сделать, чтоб аргументы у логарифмов были одинаковые?
— Вынести квадрат вперед и каким-то образом перевернуть дробь.
— Как можно перевернуть дробь?
— Можно использовать степень \(-1\).
— Что можно сделать теперь?
— Логарифмы полностью одинаковые значит можно либо сделать замену, либо вынести их за скобку.
7. Чего от меня хочет задача? Когда будет выполняться условие задачи?
Допустим, вы никогда не сталкивались с дробными неравенствами или забыли, как их решать. Давай просто порассуждаем.
— Чего от меня хочет задача?
— Чтоб левая часть была положительна.
— А когда будет положителен числитель?
— Когда икс больше трех. Если же икс меньше трех, то числитель будет иметь знак минус.
— Тот же вопрос про знаменатель?
— Знаменатель положителен при иксе большем \(1\), и отрицателен при иксе меньше \(1\).
— Так когда же будет выполняться условие задачи?
— При иксе большем \(3\) (там в дроби и сверху и снизу плюс) и при иксе меньше \(1\) (в этом случае и числитель, и знаменатель имеют знак минус).
— Чего от меня хочет задача?
— Чтоб я нашел такие иксы, при которых слева – ноль.
— А что у нас стоит слева?
— Сумма двух квадратов.
— В каком случае сумма квадратов будет равняться нулю?
— Хм… Квадрат не может быть отрицательным, он всегда больше либо равен нуля. А мы складываем два таких выражения. Значит, нам нужны такие иксы, при которых оба квадрата ОДНОВРЕМЕННО обратятся в ноль, потому что в остальных случаях сумма будет больше нуля.
8. Могу ли я сделать какую-нибудь замену?
— (вспоминаем предыдущие пункты) Какие неслучайности я вижу?
— В скобке вторая дробь – это перевернутая первая.
— Как это можно использовать?
— Ну…
— Какие преобразования тут возможны в принципе?
— О! Можно перенести всё влево и разложить на множители по формуле разности квадратов!
— Что можно теперь сделать?
— Можно привести выражения в скобках к общему знаменателю.
Итого: приучайтесь рассуждать в математике. Не мыслите шаблонами, а ищите путь. И написанные выше вопросы вам в этом помогут. Успешных решений!
10 шагов по решению задач в программировании
Это сборник советов для разработчиков-новичков, которые смотрят на пустой экран и не знают, с чего начать. Нередко можно услышать от молодых разработчиков, работающих над решением каких-то задач в программировании, что они не уверены, за что нужно хвататься. Ты понимаешь саму задачу, логику, основы синтаксиса и так далее. Если ты видишь чей-то код, или тебе кто-то помогает, то можно всё сделать самому. Но бывает, что ты не уверен в своих силах, или поначалу тебе трудно реализовать свои мысли в коде, несмотря на то, что ты знаешь синтаксис и логику. Под катом — несколько советов по решению этой проблемы, которые помогут вам в повседневной работе.
1. Прочитайте условия задачи как минимум трижды (или хотя бы столько раз, сколько вам будет удобно)
Вы не сможете решить задачу, если не поймёте её. Есть разница между задачей и задачей, которую, как вам кажется, вы решаете. Можно прочитать первые несколько строк, а насчёт остального выстроить предположения, поскольку всё выглядит похожим на то, с чем вы сталкивались раньше. Даже если вы делаете популярную игру наподобие Виселицы, удостоверьтесь, что прочитали все её правила, пусть даже вы играли в неё раньше.
Иногда можно попробовать объяснить задачу другу и посмотреть, поймёт ли он ваше объяснение. Вы же не хотите пройти половину пути и обнаружить, что неправильно поняли требования. Так что лучше потратить в начале больше времени, чтобы всё прояснить. Чем лучше поймёте задачу, тем легче будет её решить.
Какие вопросы можно себе задать:
2. Пройдите по задаче вручную как минимум с тремя наборами данных
Возьмите лист бумаги и пройдите по задаче вручную. Выберите не менее трёх наборов данных для проверки. Выберите предельно допустимые и крайние случаи.
Предельно допустимые случаи: проблема или ситуация, возникающая за пределами нормальных параметров функционирования. Например, когда одновременно несколько переменных или состояний среды имеют экстремальные значения, даже если каждый из параметров находится в своём специфическом диапазоне.
Крайние случаи: проблемы или ситуации, возникающие только при экстремальных (минимальных или максимальных) значениях параметров функционирования.
Вот, к примеру, несколько наборов данных для использования:
Когда только начинаешь, то зачастую пренебрегаешь какими-то шагами. Поскольку наш мозг уже знаком с чётными числами, то можно просто посмотреть на набор чисел и сразу передать в массив 2, 4, 6 и так далее, не думая о том, как наш мозг выбирает конкретные числа. Если вы замечаете это за собой, то лучше взять большой набор данных, чтобы помешать мозгу решать задачу, просто глядя на числа. Это поможет придерживаться настоящего алгоритма.
Давайте пройдём по массиву [1]
3. Упрощайте и оптимизируйте свой алгоритм
Поищите подходящие паттерны, может быть, что-то удастся обобщить. Подумайте, можно ли уменьшить количество шагов.
4. Пишите псевдокод
После проработки основных шагов напишите псевдокод, который можно перевести в настоящий код. Это поможет определить структуру кода, да и вообще облегчит его написание. Пишите псевдокод построчно. Это можно делать на бумаге или в виде комментариев в редакторе. Если вы только начинаете и считаете, что пустой экран выглядит жутковато или отвлекает, то лучше писать на бумаге.
В целом не существует правил для написания псевдокода, но можно включать синтаксис из вашего языка, если так будет удобнее. Но сосредотачивайтесь не на синтаксисе, а на логике и этапах алгоритма.
Вот пример псевдокода, в основном состоящего из слов:
А вот псевдокод, в котором слов гораздо меньше:
Главное, писать код построчно и понимать логику каждой строки.
Вернитесь к задаче, чтобы удостовериться, что вы на правильном пути.
5. Преобразуйте псевдокод в нормальный код и отладьте его
Когда ваш псевдокод будет готов, преобразуйте каждую строку в реальный код на вашем языке. Здесь мы воспользуемся JavaScript.
Если вы писали на бумаге, то перенесите всё в редактор в виде комментариев, а затем замените каждую строку.
Теперь вызовите функцию и дайте ей некоторые из ранее использованных наборов данных. Так можно проверить, возвращает ли код нужный результат. Также можете написать тесты для проверки соответствия выходных данных ожидаемому результату.
Ниже приведён код, полученный после обработки каждой строки псевдокода. Символы // обозначают строки из псевдокода. Жирным выделен реальный код на JavaScript.
Уберём псевдокод, чтобы не путаться.
Иногда разработчики-новички настолько увлекаются синтаксисом, что им трудно идти дальше. Помните, что со временем вам будет проще соблюдать синтаксис, и нет ничего стыдного в том, чтобы потом при написании кода обращаться к справочным материалам для корректного соблюдения синтаксиса.
6. Упрощайте и оптимизируйте код
Возможно, вы заметили, что упрощение и оптимизация — это повторяющиеся темы.
Эдсгер Дейкстра, нидерландский учёный и один из первопроходцев в ряде областей информатики
Может потребоваться несколько итераций упрощения и оптимизации кода, по мере того как вы будете находить новые способы.
Задавайте себе такие вопросы:
«Программы должны быть написаны так, чтобы люди их читали, и лишь во вторую очередь — чтобы машины их исполняли».
Джеральд Сассман и Гарольд Абельсон, авторы “Structure and Interpretation of Computer Programs”
7. Отлаживайте
Этот шаг необходимо выполнять в ходе всего процесса. Сквозная отладка поможет раньше выловить любые ошибки синтаксиса или недостатки логики. Воспользуйтесь преимуществами своего IDE (Integrated Development Environment) и отладчика. При обнаружении бага рекомендуется просматривать код построчно, стараясь найти неожиданные вещи. Несколько советов:
«Самый эффективный инструмент отладки — тщательное продумывание в сочетании с разумно размещёнными командами вывода на экран».
Брайан Керниган, профессор информатики в Принстонском университете
8. Пишите полезные комментарии
Через месяц вы можете и не вспомнить, что означает каждая строка кода. А тот, кто будет работать с вашим кодом, вообще этого не знает. Поэтому важно писать полезные комментарии, чтобы избежать проблем и сэкономить впоследствии время, когда придётся снова вернуться к этому коду.
Избегайте таких комментариев:
// Это массив. Итерируем его.
// Это переменная.
Старайтесь писать короткие, высокоуровневые комментарии, которые помогут понять, что тут происходит, если это не очевидно. Это пригодится при решении сложных задач, вы сможете быстро понять, что делает конкретная функция, и почему. Благодаря использованию понятных комментариев и имён переменных и функций вы (и другие люди) сможете понять:
9. Получайте отзывы посредством ревизии кода
Получайте отзывы от коллег, руководителей и других разработчиков. Читайте Stack Overflow. Смотрите, как другие решали аналогичные задачи и учитесь у них. Нередко бывает несколько способов решения задачи. Узнайте, что они собой представляют, и вам будет быстрее и проще приходить к ним самостоятельно.
«Неважно, насколько медленно вы пишете чистый код, вы всегда будете тратить больше времени, если пишете грязный код».
Дядя Боб Мартин, программный инженер и соавтор манифеста Agile
10. Практикуйтесь, практикуйтесь, практикуйтесь
Даже опытные разработчики постоянно практикуются и учатся. Если вы получили полезный отклик, внедрите его. Снова решите задачу, или аналогичные задачи. Заставляйте себя. С каждой решённой задачей вы становитесь лучше как разработчик. Радуйтесь каждому успеху и не забывайте, как много вы уже прошли. Помните, что программирование, как и любая деятельность, со временем будет даваться всё проще и легче.
«Гордитесь тем, сколько вы прошли. Верьте в то, что пройдёте ещё больше. Но не забывайте наслаждаться путешествием».