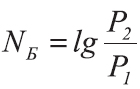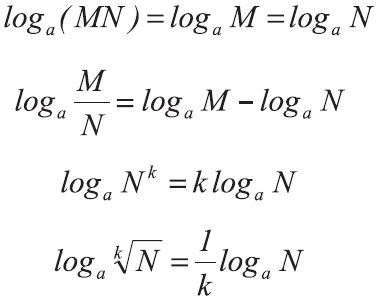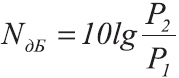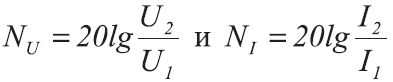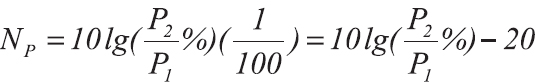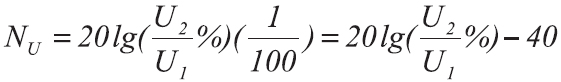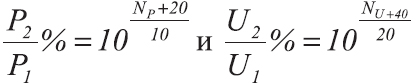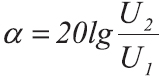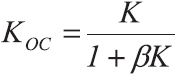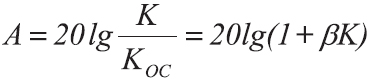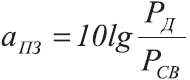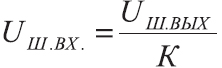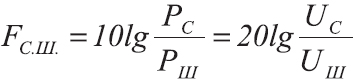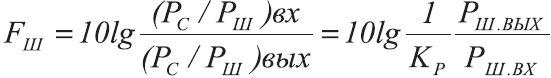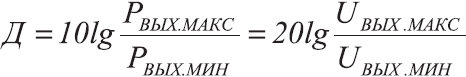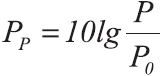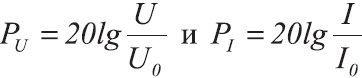Значение слова «децибел»
двух значений энергетической величины
, такой как мощность, энергия, плотность энергии и т. п., выраженное в децибелах, определяется по формуле:
Отсюда следует, что увеличение энергетической величины на 1 дБ означает её увеличение в
Энергетические величины пропорциональны квадратам силовых величин (или величин поля, как принято в международных документах), таких как звуковое давление, электрическое напряжение, сила электрического тока и т. п., поэтому отношение
двух значений силовой величины
, выраженное в децибелах, определяется по формуле:
Отсюда следует, что увеличение силовой величины на 1 дБ означает её увеличение в
Децибел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, акустике, радиотехнике.
децибе́л
1. физ. единица измерения громкости звука; десятая часть бела
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: единичность — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «децибел»
Синонимы к слову «децибел»
Предложения со словом «децибел»
Сочетаемость слова «децибел»
Понятия, связанные со словом «децибел»
Отправить комментарий
Дополнительно
Предложения со словом «децибел»
Поэтому она быстро приобрела профессиональный тон, голос физика – ясный, уверенный, громкостью на несколько децибел превышающий потребности разговора.
– Неправда. У лайнера мотор выдаёт две сотни децибел. – Никакое брюхо на такое не способно, как бы оно ни проголодалось.
Самый громкий звук, полученный в лабораторных условиях, составил двести десять децибел.
Децибел
Децибе́л — логарифмическая единица уровней, затуханий и усилений. [1]
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять:
где AdB — величина в децибелах, A — измеренная физическая величина, A0 — величина, принятая за базис.
Децибел — это безразмерная единица, применяемая для измерения отношения некоторых величин — «энергетических» (мощности, энергии, плотности потока мощности и т. п.) или «силовых» (силы тока, напряжения и т. п.). Иными словами, децибел — это относительная величина. Не абсолютная, как, например, ватт или вольт, а такая же относительная, как кратность («трёхкратное отличие») или проценты, предназначенная для измерения отношения («соотношения уровней») двух других величин, причём к полученному отношению применяется логарифмический масштаб.
Русское обозначение единицы «децибел» — «дБ», международное — «dB» [2] (неправильно: дб, Дб).
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международное бюро мер и весов рекомендовала включить его в эту систему.
Содержание
Сравнение с другими логарифмическими единицами
| название | сокращение | соответствует изменению в … раз | пересчёт в … | |||
|---|---|---|---|---|---|---|
| дБ | Б | Нп | X m | |||
| децибел | дБ, dB | ≈1,26 ( ) ) | 1 | 0,1 | ≈0,115 | −0,25 |
| бел | Б, B | 10 | 10 | 1 | ≈1,15 | −2,5 |
| непер | Нп, Np | ≈2,72 (e) | ≈8,686 | ≈0,8686 | 1 | ≈−1,086 |
| звёздная величина | X m | ≈0,398 ( ) ) | −4 | −0,4 | ≈−0,921 | 1 |
Области применения
Децибелы широко применяются в любых областях техники, где требуется измерение величин, меняющихся в широком диапазоне: в радиотехнике, антенной технике, в системах передачи информации, в оптике, акустике (в децибелах измеряется уровень громкости звука) и др. Так, в децибелах принято измерять динамический диапазон (например, диапазон громкости звучания музыкального инструмента), затухание волны при распространении в поглощающей среде, коэффициент усиления и коэффициент шума усилителя.
Децибелы используются не только для измерения отношения физических величин второго порядка (энергетических: мощность, энергия) и первого порядка (напряжение, сила тока). В децибелах можно измерять отношения любых физических величин, а также использовать децибелы для представления абсолютных величин (см. опорный уровень).
Переход к децибелам
Любые операции с децибелами упрощаются, если руководствоваться правилом: величина в дБ — это 10 десятичных логарифмов отношения двух одноименных энергетических величин. Всё остальное — следствия этого правила. «Энергетические» — величины второго порядка (энергия, мощность). По отношению к ним напряжение и сила электрического тока («неэнергетические») — величины первого порядка (P
U²), которые должны быть на каком-то этапе вычислений корректно преобразованы в энергетические. [источник не указан 153 дня]
Измерение «энергетических» величин
Изначально дБ использовался для оценки отношения мощностей, и в каноническом, привычном смысле величина, выраженная в дБ, предполагает логарифм отношения двух мощностей и вычисляется по формуле:

Соответственно, переход от дБ к отношению мощностей осуществляется по формуле:


Измерение «неэнергетических» величин
Из правила (см. выше) следует, что «неэнергетические» величины должны быть преобразованы в энергетические. Так, согласно закону Джоуля-Ленца 


В общем случае напряжения U1 и U0 могут регистрироваться на различных по величине сопротивлениях (R1 не равно R0). Такое может быть, например, при определении коэффициента усиления усилителя, имеющего различные выходное и входное сопротивления, или при измерении потерь в согласующем устройстве, трансформирующем сопротивления. Поэтому в общем случае
величина в децибелах = 
Только в частном (весьма распространенном) случае, если оба напряжения U1 и U0 измерялись на одном и том же сопротивлении (R1 = R0), можно пользоваться кратким выражением
величина в децибелах = 
Децибелы «по мощности», «по напряжению» и «по току»
Из правила (см. выше) следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R1 = R0 (в частности, если R1 и R0 — одно и то же сопротивление, или в случае, если соотношение сопротивлений R1 и R0 по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:
дБ по напряжению = 

Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует чётко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R1 не равно R0, следует пользоваться выражением для общего случая (см. выше).
Нетрудно подсчитать, что, в частности:
Примеры вычислений
Переход к дБ
Пусть значение мощности P1 стало в 2 раза больше исходного значения мощности P0, тогда
10 lg(P1/P0) = 10 lg(2) ≈3,0103 дБ ≈ 3 дБ,
то есть рост мощности на 3 дБ означает её увеличение в 2 раза.
Пусть значение мощности P1 стало в 2 раза меньше исходного значения мощности P0, то есть P1 = 0,5 P0. Тогда
то есть снижение мощности на 3 дБ означает её снижение в 2 раза. По аналогии:
Переход от дБ к «разам»
Изменение «в разах» по известному изменению в дБ (условное обозначение «dB» в формулах ниже) вычисляется следующим образом:
Переход от дБ к мощности
Для этого нужно знать значение опорного уровня мощности P0. Например, при P0 = 1 мВт и известном изменении на +20 дБ:

Переход от дБ к напряжению (току)
Для этого нужно знать значение опорного уровня напряжения U0 и определиться, регистрировалось ли напряжение на одинаковом сопротивлении, или же для решаемой задачи различие значений сопротивлений не важно. Например, при условии R0 = R1, заданном U0 = 2 В и приросте напряжения на 6 дБ:

Рекомендации
Операции с децибелами можно выполнять в уме: вместо умножения, деления, возведения в степень и извлечения корня применяется сложение и вычитание децибельных единиц. Для этого можно использовать таблицы соотношений (первые 2 — приближённые):
1 дБ → в 1,25 раза, 3 дБ → в 2 раза, 10 дБ → в 10 раз.
Отсюда, раскладывая «более сложные значения» на «составные», получаем:
6 дБ = 3 дБ + 3 дБ → в 2·2 = в 4 раза, 9 дБ = 3 дБ + 3 дБ + 3 дБ → в 2·2·2 = в 8 раз, 12 дБ = 4 · (3 дБ) → в 2 4 = в 16 раз
13 дБ = 10 дБ + 3 дБ → в 10·2 = в 20 раз, 20 дБ = 10 дБ + 10 дБ → в 10·10 = в 100 раз, 30 дБ = 3 · (10 дБ) → в 10³ = в 1000 раз
Сложению (вычитанию) значений в дБ соответствует умножение (деление) самих отношений. Отрицательные значения дБ соответствуют обратным отношениям. Например:
Причины использования децибелов
Для применения децибелов и оперирования логарифмами вместо процентов или долей есть ряд причин:
Условные обозначения
Для различных физических величин одному и тому же числовому значению, выраженному в децибелах, могут соответствовать разные уровни сигналов (вернее разности уровней). Поэтому во избежание путаницы такие «конкретизированные» единицы измерения обозначают теми же буквами «дБ», но с добавлением индекса — общепринятого обозначения измеряемой физической величины. Например дБВ (децибел относительно вольта) или дБмкВ (децибел относительно микровольта), дБВт (децибел относительно ватта) и т. п. В соответствии с международным стандартом МЭК 27-3 при необходимости указать исходную величину её значение помещают в скобках за обозначением логарифмической величины, например, для уровня звукового давления: LP (re 20 µPA) = 20 dB; LP (исх. 20 мкПа) = 20 дБ
Опорный уровень
Децибел служит для определения отношения двух величин. Но нет ничего удивительного в том, что децибел используют и для измерения абсолютных значений. Для этого достаточно условиться, какой уровень измеряемой физической величины будет принят за опорный уровень (условный 0 дБ).
Строго говоря, должно быть однозначно определено, какая именно физическая величина и какое именно её значение используются в качестве опорного уровня. Опорный уровень указывается в виде добавки, следующей за символами «дБ» (например, дБм), либо опорный уровень должен быть ясен из контекста (например, «дБ относительно 1 мВт»).
На практике распространены следующие опорные уровни и специальные обозначения для них:
По аналогии образуются составные единицы измерений. Например, уровень спектральной плотности мощности дБВт/Гц — «децибельный» аналог единицы измерения Вт/Гц (мощность, выделяющаяся на номинальной нагрузке в полосе частот шириной в 1 Гц с центром на указанной частоте). Опорным уровнем в данном примере является 1 Вт/Гц, то есть физическая величина «спектральная плотность мощности», её размерность «Вт/Гц» и значение «1». Так, запись «-120 дБВт/Гц» полностью эквивалентна записи «10 −12 Вт/Гц».
В случае затруднения во избежание путаницы достаточно указать опорный уровень явно. Например, запись −20 дБ (относительно 0,775 B на нагрузке 50 Ом) исключает двойное толкование.
Справедливы следующие правила (следствие правил действий с размерными величинами):
При пересчёте уровней мощностей (дБВт, дБм) в уровни напряжений (дБВ, дБмкВ) и обратно необходимо учитывать сопротивление, на котором определяется мощность и напряжение:
ПРИМЕНЕНИЕ ДЕЦИБЕЛ В РАДИОЭЛЕКТРОНИКЕ И ЭЛЕКТРОАКУСТИКЕ
ЧТО ТАКОЕ ДЕЦИБЕЛЫ?
Универсальные логарифмические единицы децибелы широко используются при количественных оценках параметров различных аудио и видео устройств в нашей стране и за рубежом. В радиоэлектронике, в частности, в проводной связи, технике записи и воспроизведения информации децибелы являются универсальной мерой.
Децибел — не физическая величина, а математическое понятие
В электроакустике децибел служит по существу единственной единицей для характеристики различных уровней — интенсивности звука, звукового давления, громкости, а также для оценки эффективности средств борьбы с шумами.
Децибел — специфическая единица измерений, не схожая ни с одной из тех, с которыми приходится встречаться в повседневной практике. Децибел не является официальной единицей в системе единиц СИ, хотя, по решению Генеральной конференции по мерам и весам, допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.
Децибел — не физическая величина, а математическое понятие.
В этом отношении у децибел есть некоторое сходство с процентами. Как и проценты, децибелы безразмерны и служат для сравнения двух одноименных величин, в принципе самых различных, независимо от их природы. Следует отметить, что термин «децибел» всегда связывают только с энергетическими величинами, чаще всего с мощностью и, с некоторыми оговорками, с напряжением и током.
Бел — это десятичный логарифм отношения двух мощностей. Если известны две мощности Р1 и Р2, то их отношение, выраженное в белах, определяется формулой:
Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п.
Напомним вкратце, что такое логарифм. Любое положительное 2 число, как целое, так и дробное, можно представить другим числом в определенной степени.
Так, например, если 10 2 = 100, то 10 называют основанием логарифма, а число 2 — логарифмом числа 100 и обозначают log10 100=2 или lg 100 = 2 (читается так: «логарифм ста при основании десять равен двум»).
Логарифмы с основанием 10 называются десятичными логарифмами и применяются чаще всего. Для чисел, кратных 10, этот логарифм численно равен количеству нулей за единицей, а для остальных чисел вычисляется на калькуляторе или находится по таблицам логарифмов.
Логарифмы с основанием е = 2,718. называются натуральными. В вычислительной технике обычно применяются логарифмы с основанием 2.
Основные свойства логарифмов:
Разумеется, эти свойства справедливы и для десятичных и натуральных логарифмов. Логарифмический способ представления чисел часто оказывается очень удобным, так как позволяет подменять умножение — сложением, деление — вычитанием, возведение в степень умножением, а извлечение корня — делением.
На практике бел оказался слишком крупной величиной, например, любые отношения мощностей в границах от 100 до 1000 укладываются в пределах одного бела — от 2 Б до 3 Б. Поэтому для большей наглядности решили число, показывающее количество бел, умножать на 10 и полученное произведение считать показателем в децибелах, т. е., например, 2 Б = 20 дБ, 4,62 Б = 46,2 дБ и т. д.
Обычно отношение мощностей выражают сразу в децибелах по формуле:
Действия с децибелами не отличаются от операций с логарифмами.
Нетрудно посчитать, что 1 дБ соответствует отношению мощностей примерно равному 1,259 или 26%.
2 дБ = 1 дБ + 1 дБ → 1,259 * 1,259 = 1,585;
3 дБ → 1,259 3 = 1,995;
4 дБ → 2,512;
5 дБ → 3,161;
6 дБ → 3,981;
7 дБ → 5,012;
8 дБ → 6,310;
9 дБ → 7,943;
10 дБ → 10,00.
Знак → означает «соответствует».
Подобным образом можно составить таблицу и для отрицательных значений децибел. Минус 1 дБ характеризует убывание мощности в 1/0,794 = 1,259 раза, т. е. тоже примерно на 26%.
И еще одна особенность: кривая, определяющая значения децибел в зависимости от отношений мощностей, вначале быстро растет, затем ее рост замедляется.
Зная число децибел, соответствующих одному отношению мощностей, можно произвести пересчет для другого — близкого или кратного отношения. В частности, для отношений мощностей, различающихся в 10 раз, число децибел отличается на 10 дБ. Эту особенность децибел следует хорошо понять и твердо запомнить — она является одной из основ всей системы
К достоинствам системы децибел относят:
⇒ универсальность, т. е. возможность использования при оценке различных параметров и явлений;
⇒ огромные перепады преобразуемых чисел — от единиц и до миллионов — отображаются в децибелах числами первой сотни;
⇒ натуральные числа, представляющие степени десяти, выражаются в децибелах числами, кратными десяти;
⇒ взаимообратные числа выражаются в децибелах равными числами, но с разными знаками;
⇒ в децибелах могут быть выражены как отвлеченные, так и именованные числа.
К недостаткам системы децибел относят:
⇒ малую наглядность: для преобразования децибел в отношения двух чисел или выполнения обратных действий требуется проведение расчетов;
⇒ отношения мощностей и отношения напряжений (или токов) пересчитываются в децибелы по разным формулам, что иногда ведет к ошибкам и путанице;
⇒ децибелы могут отсчитываться только относительно не равного нулю уровня; абсолютный нуль, например 0 Вт, 0 В, децибелами не выражается.
Зная число децибел, соответствующих одному отношению мощностей, можно произвести пересчет для другого — близкого или кратного отношения. В частности, для отношений мощностей, различающихся в 10 раз, число децибел отличается на 10 дБ. Эту особенность децибел следует хорошо понять и твердо запомнить — она является одной из основ всей системы.
Сравнение двух сигналов путем сопоставления их мощностей не всегда бывает удобным, так как для непосредственного измерения электрической мощности в диапазоне звуковых и радиочастот требуются дорогие и сложные приборы. На практике при работе с аппаратурой гораздо проще измерять не мощность, которая выделяется на нагрузке, а падение напряжения на ней, а в некоторых случаях — протекающий ток.
Зная напряжение или ток и сопротивление нагрузки, легко определить мощность. Если измерения проводятся на одном и том же резисторе, то:
Этими формулами очень часто пользуются практике, но обратите внимание, что если напряжения или токи измеряются на разных нагрузках, эти формулы не работают и следует использовать другие, более сложные зависимости.
Пользуясь приемом, который был использован при составлении таблицы децибел мощности, можно аналогично определить, чему равен 1 дБ отношения напряжений и токов. Положительный децибел будет равен 1,122, а отрицательный децибел будет равен 0,8913, т.е. 1 дБ напряжения или тока характеризует возрастание или убывание этого параметра примерно на 12% по отношению к первоначальному значению.
Формулы выводились в предположении, что сопротивления нагрузок имеют активный характер и между напряжениями или токами нет фазового сдвига. Строго говоря, следовало бы рассматривать общий случай и учитывать для напряжений (токов) наличие угла сдвига по фазе, а для нагрузок не только активное, но полное сопротивление, включая и реактивные составляющие, однако это существенно только на высоких частотах.
Полезно запомнить некоторые часто встречающиеся на практике значения децибел и характеризующие их отношения мощностей и напряжений (токов), приведенные в табл. 1.
Таблица 1. Часто встречающиеся значения децибел мощности и напряжения
| ± дБ | 1 | 3 | 10 | 20 | 30 | |
| Р2/Р1 | 1,26 (0,79) | 2 (0,5) | 10 (0,1) | 100 (0,01) | 1000 (0,001) | |
| ± дБ | 1 | 3 | 6 | 10 | 20 | 40 |
| U2/U1 или I2/I1 | 1,12 (0,9) | 1,41 (0,707) | 2 (0,5) | 3,16 (0,316) | 10 (0,1) | 100 (0,01) |
Пользуясь этой таблицей и свойствами логарифмов легко подсчитать, чему соответствуют произвольные значения логарифм. Например, 36 дБ мощности можно представить как 30+3+3, что соответствует 1000*2*2 = 4000. Тот же самый результат мы получим, представив 36 как 10+10+10+3+3 → 10*10*10*2*2 = 4000.
СОПОСТАВЛЕНИЕ ДЕЦИБЕЛ С ПРОЦЕНТАМИ
Ранее отмечалось, что понятие децибел имеет некоторое сходство с процентами. Действительно, так как в процентах выражается отношение какого-то числа к другому, условно принятому за сто процентов, отношение этих чисел также можно представить в децибелах при условии, что оба числа характеризуют мощность, напряжение или ток. Для отношения мощностей:
Для отношения напряжений или токов:
Можно также вывести формулы для пересчета децибел в проценты отношения:
В табл. 2 дан перевод некоторых, наиболее часто встречающихся значений децибел в проценты отношений. Различные промежуточные значения можно найти по номограмме на рис. 1.
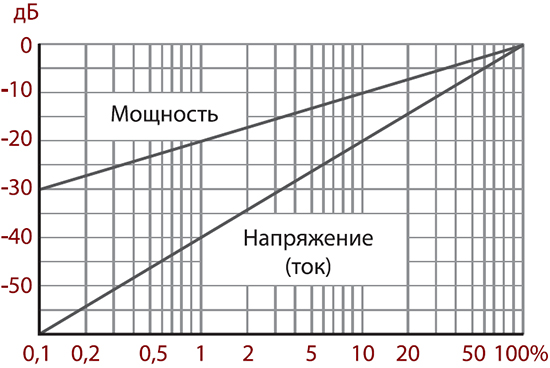
Рис. 1. Перевод децибел в проценты отношений по номограмме
Таблица 2. Перевод децибел в проценты отношений
| % | 100 | 50 | 10 | 1 | 0,1 |
| NU или NI | 0 | -6 | -20 | -40 | -60 |
| NP | 0 | -3 | -10 | -20 | -30 |
Рассмотрим два практических примера, поясняющих перевод процентного отношения в децибелы.
Пример 1. Какому уровню гармоник в децибелах по отношению к уровню сигнала основной частоты соответствует коэффициент нелинейных искажений в 3%?
Воспользуемся рис. 1. Через точку пересечения вертикальной линии 3% с графиком «напряжение» проведем горизонтальную линию до пересечения с вертикальной осью и получим ответ: –31 дБ.
Пример 2. Какому ослаблению напряжения в процентах соответствует его изменение на –6 дБ?
Ответ. На 50% первоначальной величины.
В практических расчетах дробную часть численного значения децибел часто округляют до целого числа, однако при этом в результаты расчетов вносится дополнительная погрешность.
ДЕЦИБЕЛЫ В РАДИОЭЛЕКТРОНИКЕ
Рассмотрим несколько примеров, поясняющих методику использования децибел в радиоэлектронике.
Затухание в кабеле
Потери энергии в линиях и кабелях на единицу длины характеризуются коэффициентом затухания α, который при равном входном и выходном сопротивлениях линии определяется в децибелах:
где U1 — напряжение в произвольном сечении линии; U2 — напряжение в другом сечении, отстоящем от первого на единицу длины: 1 м, 1 км и т. д. Например, высокочастотный кабель типа РК-75-4-14 имеет на частоте 100 МГц коэффициент затухания α, = –0,13 дБ/м, кабель витой пары категории 5 на той же частоте имеет затухание порядка –0,2 дБ/м, а у кабеля категории 6 несколько меньше. График затухания сигнала в неэкранированном кабеле витой пары показан на рис. 2.
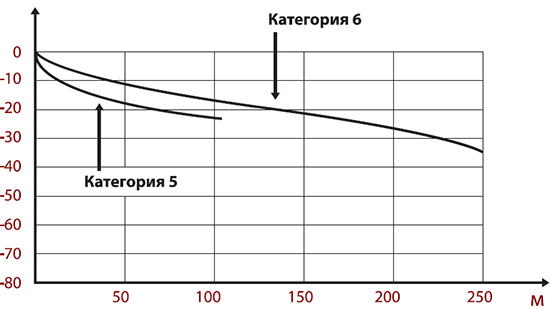
Рис. 2. График затухания сигнала в неэкранированном кабеле витой пары
Оптоволоконные кабели имеют существенно более низкие величины затухания в диапазоне от 0,2 до 3 дБ при длине кабеля в 1000 м. Все оптические волокна имеют сложную зависимость затухания от длины волны, которая имеет три «окна прозрачности» 850 нм, 1300 нм и 1550 нм. «Окно прозрачности» означает наименьшие потери при максимальной дальности передачи сигнала. График затухания сигнала в оптоволоконных кабелях показан на рис. 3.
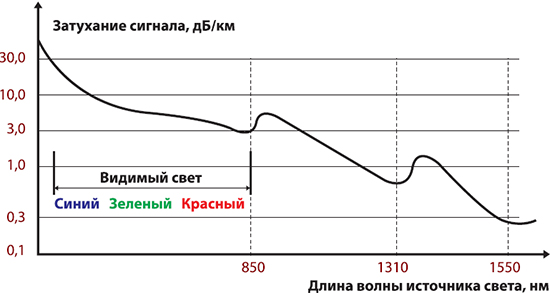
Рис. 3. График затухания сигнала в оптоволоконных кабелях
Пример 3. Найти, каким будет напряжение на выходе отрезка кабеля РК-75-4-14 длиной l = 50 м, если ко входу его приложено напряжение 8 В частоты 100 МГц. Сопротивление нагрузки и волновое сопротивление кабеля равны, или, как говорят, согласованы между собой.
Очевидно, что затухание, вносимое отрезком кабеля, составляет K = –0,13 дБ/м * 50 м = –6,5 дБ. Это значение децибел примерно соответствует отношению напряжений 0,47. Значит, напряжение на выходном конце кабеля U2 = 8 В * 0,47 = 3,76 В.
Этот пример иллюстрирует очень важное положение: потери в линии или кабеле с ростом их длины возрастают чрезвычайно быстро. Для отрезка кабеля длиной в 1 км затухание составит уже –130 дБ, т. е. сигнал будет ослаблен более чем в триста тысяч раз!
Затухание в значительной мере зависит от частоты сигналов — в диапазоне звуковых частот оно будет гораздо меньше, чем в видео диапазоне, но логарифмический закон затухания будет тот же, и при большой длине линии ослабление будет существенным.
Усилители звуковой частоты
В усилители звуковой частоты с целью повышения их качественных показателей обычно вводится отрицательная обратная связь. Если коэффициент усиления устройства по напряжению без обратной связи равен К, а с обратной связью КОС то число, показывающее, во сколько раз изменяется коэффициент усиления под действием обратной связи, называют глубиной обратной связи. Ее обычно выражают в децибелах. В работающем усилителе коэффициенты К и КОС определяются экспериментально, если только усилитель не возбуждается при разомкнутой петле обратной связи. При проектировании усилителя сначала вычисляют К, а затем определяют значение КОС следующим образом:
где β — коэффициент передачи цепи обратной связи, т. е. отношение напряжения на выходе цепи обратной связи к напряжению на ее входе.
Глубина обратной связи в децибелах может быть рассчитана по формуле:
Стереофонические устройства по сравнению с монофоническими должны удовлетворять дополнительным требованиям. Эффект объемного звучания обеспечивается только при хорошем разделении каналов, т. е. при отсутствии проникновения сигналов из одного канала в другой. В практических условиях это требование полностью удовлетворить не удается, и взаимное просачивание сигналов имеет место, главным образом, через узлы, общие для обоих каналов. Качество разделения по каналам характеризуется так называемым переходным затуханием аПЗ Мерой переходного затухания в децибелах служит отношение выходных мощностей обоих каналов, когда входной сигнал подается только на один канал:
где РД — максимальная выходная мощность действующего канала; РСВ — выходная мощность свободного канала.
Хорошему разделению каналов соответствует переходное затухание 60—70 дБ, отличному –90—100 дБ.
Шум и фон
На выходе любого приемно-усилительного устройства даже при отсутствии полезного входного сигнала можно обнаружить переменное напряжение, которое вызвано собственными шумами устройства. Причины, вызывающие собственные шумы, могут быть как внешними — за счет наводок, плохой фильтрации напряжения питания, так и внутренними, обусловленными собственными шумами радиокомпонентов. Сильнее всего сказываются шумы и, помехи, возникающие во входных цепях и в первом усилительном каскаде, так как они усиливаются всеми последующими каскадами. Собственные шумы ухудшают реальную чувствительность приемника или усилителя.
Количественная оценка шумов осуществляется несколькими способами.
Простейший состоит в том, что все шумы, независимо от причины и места их возникновения, пересчитываются ко входу, т. е. напряжение шумов на выходе (при отсутствии входного сигнала) делится на коэффициент усиления:
Это напряжение, выраженное в микровольтах, и служит мерой собственных шумов. Однако для оценки устройства с точки зрения помех важно не абсолютное значение шумов, а отношение между полезным сигналом и этим шумом (отношение сигнал/шум), так как полезный сигнал должен надежно выделяться на фоне помех. Отношение сигнал/шум обычно выражают в децибелах:
где Рс — заданная или номинальная выходная мощность полезного сигнала вместе с шумом; Рш — выходная мощность шумов при выключенном источнике полезного сигнала; Uc — напряжение сигнала и шумов на нагрузочном резисторе; UШ — напряжение шумов на том же резисторе. Так получается т.н. «невзвешенное» («unweighted») отношение сигнал/шум.
Часто в параметрах аудиоаппаратуры приводится отношение сигнал/шум, измеренное со взвешивающим фильтром («weighted»). Фильтр позволяет учесть разную чувствительность слуха человека к шуму на разных частотах. Чаще всего используется фильтр типа А, в этом случае в обозначении обычно указывается единица измерения «дБА» («dBA»). Использование фильтра дает обычно лучшие количественные результаты, чем для невзвешенного шума (обычно отношение сигнал/шум получается на 6—9 дБ больше), поэтому (из маркетинговых соображений) производители аппаратуры чаще указывают именно «взвешенное» значение. Подробнее о взвешивающих фильтрах см. ниже в разделе «Шумомеры».
Очевидно, что для успешной эксплуатации устройства отношение сигнал/шум должно быть выше какого-то минимально допустимого значения, которое зависит от назначения и требований, предъявляемых к устройству. Для аппаратуры класса Hi-Fi этот параметр должен быть не менее 75 дБ, для аппаратуры Hi-End — не менее 90 дБ.
Иногда на практике пользуются обратным отношением, характеризуя им уровень шумов относительно полезного сигнала. Уровень шумов выражается тем же числом децибел, что и отношение сигнал/шум, но с отрицательным знаком.
В описаниях приемно-усилительной аппаратуры иногда фигурирует термин уровень фона, который характеризует в децибелах отношение составляющих напряжения фона к напряжению, соответствующему заданной номинальной мощности. Составляющие фона кратны частоте питающей сети (50, 100, 150 и 200 Гц) и при измерении выделяются из общего напряжения помех при помощи полосовых фильтров.
Отношение сигнал/шум не позволяет, однако, судить о том, какая часть шумов обусловлена непосредственно элементами схемы, а какая внесена в результате несовершенства конструкции (наводки, фон). Для оценки шумовых свойств радиокомпонентов вводится понятие коэффициента (фактора) шума. Коэффициент шума оценивается по мощности и также выражается в децибелах. Характеризовать этот параметр можно следующим образом. Если на входе устройства (приемника, усилителя) одновременно действуют полезный сигнал мощностью Рс и шумы мощностью Рш, то отношение сигнал/шум на входе будет (Рс/Рш)вх После усиления отношение (Рс/Рш)вых окажется меньше, так как к входным шумам добавятся и усиленные собственные шумы усилительных каскадов.
Коэффициентом шума называют выраженное в децибелах отношение:
Следовательно, коэффициент шума представляет отношение мощности шумов на выходе к усиленной мощности шумов, действующих на входе.
Для транзисторов и ИС, предназначенных для работы в первых каскадах усилительных устройств, коэффициент шума регламентируется и приводится в справочниках.
Напряжение собственных шумов определяет и другой важный параметр многих усилительных устройств — динамический диапазон.
Динамический диапазон и регулировки
Динамическим диапазоном называется выраженное в децибелах отношение максимальной неискаженной выходной мощности к ее минимальному значению, при котором, еще обеспечивается допустимое отношение сигнал/шум:
Чем меньше уровень собственных шумов и чем выше неискаженная выходная мощность, тем шире динамический диапазон.
Аналогичным образом определяется и динамический диапазон источников звука — оркестра, голоса, только здесь минимальная мощность звука определяется шумовым фоном. Чтобы устройство могло передать без искажений как минимальную, так и максимальную амплитуды входного сигнала, его динамический диапазон должен быть не меньше динамического диапазона сигнала. В случаях, когда динамический диапазон входного сигнала превышает динамический диапазон устройства, его искусственно сжимают. Так поступают, например, при звукозаписи.
Эффективность действия ручного регулятора громкости проверяется при двух крайних положениях регулятора. Сначала при регуляторе в положении максимальной громкости на вход усилителя звуковой частоты подается напряжение частотой 1 кГц такой величины, чтобы на выходе усилителя установилось напряжение, соответствующее некоторой заданной мощности. Затем ручку регулятора громкости переводят на минимальную громкость, а напряжение на входе усилителя поднимают до тех пор, пока напряжение на выходе снова не станет равным первоначальному. Отношение входного напряжения при регуляторе в положении минимальной громкости к входному напряжению при максимальной громкости, выраженное в децибелах, является показателем работы регулятора громкости.
Приведенными примерами далеко не исчерпываются практические случаи приложения децибел к оценке параметров радиоэлектронных устройств. Зная общие правила, применения этих единиц, можно понять, как они используются в других, не рассмотренных здесь условиях. Встретившись с незнакомым термином, определенным в децибелах, следует отчетливо представить, отношению каких двух величин он соответствует. В одних случаях это понятно из самого определения, в других случаях связь между составляющими сложнее, и, когда нет четкой ясности, следует обратиться к описанию методики измерения во избежание серьезных ошибок.
Оперируя с децибелами, следует всегда обращать внимание на то, отношению каких единиц — мощности или напряжения — соответствует каждый конкретный случай, т. е. какой коэффициент — 10 или 20 — должен стоять перед знаком логарифма.
ЛОГАРИФМИЧЕСКИЙ МАСШТАБ
Логарифмическая система, в том числе и децибелы, часто применяется при построении амплитудно-частотных характеристик (АЧХ) — кривых, изображающих зависимость коэффициента передачи различных устройств (усилителей, делителей, фильтров) от частоты внешнего воздействия. Для построения частотной характеристики расчетным или опытным путем определяется ряд точек, характеризующих выходное напряжение или мощность при неизменном входном напряжении на разных частотах. Плавная кривая, соединяющая эти точки, характеризует частотные свойства устройства или системы.
Если по оси частот численные значения откладывать в линейном масштабе, т. е. пропорционально их фактическим значениям, то такая частотная характеристика окажется неудобной для пользования и не будет наглядной: в области низших частот она сжата, а высших — растянута.
Частотные характеристики строятся обычно в так называемом логарифмическом масштабе. По оси частот в удобном для работы масштабе откладываются величины, пропорциональные не самой частоте f, а логарифму lgf/fo, где fо — частота, соответствующая началу отсчета. Против отметок на оси надписываются значения f. Для построения логарифмических АЧХ используют специальную логарифмическую миллиметровую бумагу.
При проведении теоретических расчетов обычно пользуются не просто частотой f, а величиной ω = 2πf которую называют круговой частотой.
Частота fо, соответствующая началу отсчета, может быть сколь угодно малой, но не может быть равной нулю.
По вертикальной оси откладываются в децибелах либо в относительных числах отношения коэффициентов передачи при различных частотах к его максимальному либо среднему значению.
Логарифмический масштаб позволяет на небольшом отрезке оси отобразить широкий диапазон частот. На такой оси одинаковым отношениям двух частот соответствуют равные по длине участки. Интервал, характеризующий рост частоты в десять раз, называют декадой; двукратному отношению частот соответствует октава (этот термин заимствован из теории музыки).
Если полоса в одну октаву слишком широка, то можно применять интервалы с меньшим отношением частот в пол-октавы или трети октавы.
Средняя частота октавы (полуоктава) не равна среднему арифметическому от нижней и верхней частот октавы, а равна 0,707 fВ.
Частоты, найденные подобным образом, называют среднеквадратичными.
Для двух соседних октав средние частоты также образуют октавы. Пользуясь этим свойством, можно по желанию один и тот же логарифмический ряд частот считать либо границами октав, либо их средними частотами.
На бланках с логарифмической сеткой средняя частота делит октавный ряд пополам.
На оси частот в логарифмическом масштабе на каждую треть октавы приходятся равные отрезки оси, каждый длиной в одну треть октавы.
При испытаниях электроакустической аппаратуры и проведении акустических измерений рекомендуется применять ряд предпочтительных частот. Частоты этого ряда являются членами геометрической прогрессии со знаменателем 1,122. Для удобства значения некоторых частот округлены в пределах ±1%.
Интервал между рекомендованными частотами составляет одну шестую октавы. Сделано это не случайно: ряд содержит достаточно большой набор частот для разных видов измерений и вбирает ряды частот с интервалами в 1/3, 1/2 и целую октаву.
И еще одно важное свойство ряда предпочтительных частот. В некоторых случаях в качестве основного интервала частот используется не октава, а декада. Так вот, предпочтительный ряд частот в равной мере можно рассматривать и как двоичный (октавный), и как десятичный (декадный).
Знаменатель прогрессии, на основе которой построен предпочтительный ряд частот, численно равен 1дБ напряжения, или 1/2 дБ мощности.
ПРЕДСТАВЛЕНИЕ ИМЕНОВАННЫХ ЧИСЕЛ В ДЕЦИБЕЛАХ
До сих пор мы полагали, что и делимое и делитель под знаком логарифма имеют произвольную величину и для выполнения децибельного пересчета важно знать только их отношение независимо от абсолютных значений.
В децибелах можно выражать также конкретные значения мощностей, а также напряжений и токов. Когда величина одного из членов, стоящих под знаком логарифма в рассмотренных ранее формулах задана, второй член отношения и числа децибел будут однозначно определять друг друга. Следовательно, если задаться какой-либо эталонной мощностью (напряжением, током) в качестве условного уровня сравнения, то другой мощности (напряжению, току), сопоставляемой с ней, будет соответствовать строго определенное число децибел. Нулю децибел в этом случае отвечает мощность, равная мощности условного уровня сравнения, так как при NP= 0 Р2=Р1 поэтому этот уровень обычно называют нулевым. Очевидно, что при разных нулевых уровнях одна и та же конкретная мощность (напряжение, ток) будут выражаться разными числами децибел.
где Р — мощность, подлежащая преобразованию в децибелы, а Р0 — нулевой уровень мощности. Величина Р0 ставится в знаменателе, при этом положительными децибелами выражаются мощности Р > Р0.
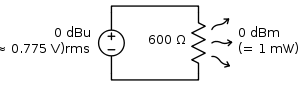
Условный уровень мощности, с которым производится сравнение, в принципе может быть любым, однако не каждый был бы удобен для практического использования. Чаще всего за нулевой уровень выбирается мощность в 1 мВт, рассеиваемая на резисторе сопротивлением 600 Ом. Выбор этих параметров произошел исторически: первоначально децибел как единица измерения появился в технике телефонной связи. Волновое сопротивление воздушных двухпроводных линий из меди близко к 600 Ом, а мощность в 1 мВт развивает без усиления высококачественный угольный телефонный микрофон на согласованном сопротивлении нагрузки.
Тот факт, что децибелы представляемого параметра отчитываются относительно определенного уровня, подчеркивают термином «уровень»: уровень помех, уровень мощности, уровень громкости
Пользуясь этой формулой, легко найти, что относительно нулевого уровня 1 мВт мощность 1 Вт определяется как 30 дБ, 1 кВт как 60 дБ, а 1 МВт — это 90 дБ, т. е. практически все мощности, с которыми приходится встречаться, укладываются в пределах первой сотни децибел. Мощности, меньшие 1 мВт, будут выражаться отрицательными числами децибел.
Децибелы, определенные относительно уровня 1 мВт, называют децибел-милливаттом и обозначают дБм или dBm. Наиболее распространенные значения нулевых уровней сведены в таблицу 3.
Аналогичным образом можно представить формулы для выражения в децибелах напряжений и токов: