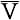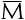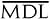Как пишется 1 миллиард цифрами?
Этот вопрос мне задавала моя дочка, когда ещё в первый класс не поступила.
Я ей ответила, что в числе этом тысяча миллионов, а пишется оно как единичка и девять нолей. Если арабскими цифрами, тогда это выглядит так: 1000 000 000.
Для того, чтобы написать один миллиард цифрами, мы должны вспомнить, что
Один миллион пишется с шестью нулями, то есть 1 000 000.
Один миллиард пишется с девятью нулями, то есть 1 000 000 000.
Один триллион пишется с двенадцатью нулями, то есть 1 000 000 000 000.
Один квадриллион пишется с пятнадцатью нулями, то есть 1 000 000 000 000 000.
Если один миллион- это единица и шесть нулей 1 000 000;
десять миллионов-единица и семь нулей 10 000 000;
сто миллионов- единица и восемь нулей 100 000 000;
Получается один миллиард-это единица и девять нулей 1 000 000 000.
Один миллиард состоит из одной тысячи миллионов, а, раз в одном миллионе шесть нулей, то, значит, добавляем к одной тысяче еще шесть нулей и получаем цифру 1 000 000 000, то есть одна единица и девять нулей.
Автор задал вопрос, написал этот вопрос без ошибок. Но. почему то не знает как написать миллиард цифрами. Может быть здесь какой то подвох? Может быть. Но я не знаю иного ответа, как вот этот: 1 000 000 000. Единица и девять нулей. Вот собственно и все!
А вот миллиард следующее за миллионом триадное число, то миллиард число с девятью нулями.А значащая единица будет десятая цифра в миллиарде.Тогда :
1 миллиард = 1 000 000 000.
То есть число с девятью нулями и с десятью цифрами.
Добрый день. Миллиард часто встречается в новостях, особенно когда пишут про бюджет, но если вас интересуют цифры, то ими написать это число просто. В нем насчитывается девять нулей, а именно 1 000 000 000.
Это крайне практическое знание. На разделении многозначного числа на 2 простых сомножителя построено 2/3 современной криптографии. Точнее не на разделении, а на сложности этого разделения.
Но начинается все с деления на 2, на 3 и тд.
Для начала нужно вспомнить как определяются умножение и возведение в степень в обычной математике. Умножение это многократное сложение, а возведение в степень это многократное умножение. Кнут предложил продолжить такие операции, например, многократное возведение в степень. Он его обозначил стрелкой вверх. Например,
Как видим таким способом мы можем кратко записать очень большие числа и главное в один ряд.
1 = 1\2015+ 1\21015+. +1\2015 15 таких дробей.Это один из вариантов.
Другой вариант более сложный:начинается решение с известного равенства :1=1\2+1\3+1\6.Потом 1\6 представляют как сумму дробей, представленных для 1\6, только с числителем тоже 1, а в знаменателях будет делённое на 6:1= 1/(2*6)+1/(3*6)+1/(6*6) = 1/12+1/18+1/36.Далее так же, то есть: 1/366получим 1/6 поделив на 6 и получим:/(12*6)+1/(18*6)+1/(36*6)..И так далее.То есть берём крайнюю дробь, каждый раз делим на 6 и пошло так дальше.Сколько таких преобразований нужно, когда получим 2015 дробей, а это будет через (примерно)2015\3=670 раз и одну дробь не преобразовывать.Сколько хочешь таких дробей можно получить.
Большая таблица Римских цифр от 1 до 1000
* Римские цифры — это натуральные числа, записанные при помощи повторения 7 латинских букв, в определённой прописанной правилами последовательности: I (1), V (5), X (10), L (50), C (100), D (500), M (1000)
| Буквы | Значения |
| I (лат. unus, unum) | 1 |
| V (лат. quinque) | 5 |
| X (лат. decem) | 10 |
| L (лат. quinquaginta) | 50 |
| C (лат. centum) | 100 |
| D (лат. quingenti) | 500 |
| M (лат. mille) | 1000 |
Если большая цифра написана перед меньшей, их складывают.
| VI | 6 (5+1) |
| XV | 15 (10+5) |
| LX | 60 (50+10) |
| CL | 150 (100+50) |
Если меньшая цифра написана перед большей (она не повторяется), тогда от большей отнимают меньшую. Вычитается 1 или степени 10.
| IV | 4 (5-1) |
| IX | 9 (10-1) |
| XL | 40 (50-10) |
| XC | 90 (100-10) |
Цифры V, L и D не повторяются, а I, X, C и M могут повторно использоваться до 3 раз.
| VIII | 8 |
| LXXX | 80 |
| DCCC | 800 |
| MMMD | 3500 |
Римскими цифрами можно записывать и большие числа. Над цифрой сверху, значение которой нужно увеличить в 1000 раз ставят черту.
Римские цифры от 1 до 1000
В процессе жизнедеятельности мы время от времени встречаемся с римскими цифрами от 1 до 1000, некогда популярными в Римской империи и Средневековье. Они используются для обозначения количества веков или тысячелетий, группы крови на формах военнослужащих, количества томов в книгах, валентности в группе химических элементов и многого другого. Будучи популярными в начале нашей эры, они постепенно утратили пальму первенства, и ныне используются спорадически, под влиянием традиций или церемониала. Каковы же римские цифры в диапазоне 1 — 1000, в чём их особенность, и почему они уступили своим восточным, арабо-индийским, конкурентам? Давайте разбираться.
Римские цифры — генезис
Римские цифры (их часто ошибочно называют «латинскими») являются разработкой и достоянием Римской цивилизации. Древние римляне создали их для облегчения счёта, дабы проще и удобнее считать разнообразные товары и услуги.
Римские цифры широко использовались в ходе существования единого римского государства, а также после его раскола на Западную и Восточную Римскую Империю. Даже после падения Константинополя они продолжали использоваться в различных варварских королевствах вплоть до конца Средневековья, пока постепенно не проиграли соперничество арабо-индийским цифрам, доминирующим по сей день.
Представление римских цифр от 1 до 1000
Римские цифры представлены семью различными буквами — I, V, X, L, C, D и M, каждая из которых обозначает какое-либо число.
Запомнить римские цифры в границах от 1 до 1000 можно с помощью следующего словосочетания (в порядке убывания):
Также вас может заинтересовать наш материал, посвящённый римским цифрам от 1 до 20.
Указанные семь букв используются для представления множества различных чисел, обычно с помощью суммирования. К примеру, римское число 2 пишется как «II» (просто две единички добавленные вместе). Число 12 – как XII, то есть X+II. Ну а номер 27 пишется как XXVII, то есть как сочетание XX + V + II.
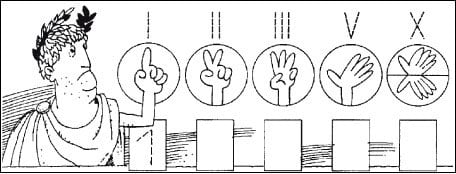
Римские цифры удобно отображались пальцами
Как видим, римские цифры записываются начиная от самой большой цифры и заканчивая маленькой, слева направо. Однако, это ещё не всё. Римляне очень не любили 4 однотипных цифры в ряду, поэтому они разработали специальную систему вычитания.
В римских цифрах число 3 пишется как «III». Однако, цифра для числа 4 будет не «IIII», так как здесь находятся четыре однотипных символа, и необходимо использовать принцип вычета. Римскими цифрами число 4 будет записываться как «IV», то есть номера 1 и 5. Поскольку меньшая цифра (1) стоит перед большей (5), то мы из большей цифры вычитываем меньшую, и получаем 4. Тот же принцип используется в отношении номера «9», который в римской системе записывается как «IX» (1 и 10)
Вот ещё шесть аналогичных примеров, позволяющих использовать римские числа от 1 до 1000:
Номер 1994 является отличным примером для данного правила. В римских цифрах оно выглядит как MCMXCIV, то есть M = 1000, CM = 900, XC = 90 и IV = 4.
Года и даты
Для записи года в римских цифрах от 1 до 1000 нам нужны большие цифры. К примеру, запись 2020 года мы начинаем с ММ (2000), добавляем ХХ (20) и получаем ММХХ.
Года из 20 столетия получить так же просто. Мы начинаем с цифры 1900 (МСМ), к которой добавляем требуемое количество лет. Например, 1985 год будет выглядеть как МСМ (1900) LXXX (80) + V (5) = MCMLXXXV.
Большие римские цифры
Поскольку цифра М (1000) — наибольшая в системе римских чисел, и мы можем использовать лишь три одинаковых символа при создании числа, то максимальное число, представленное в римской системе – это 3999 (MMMCMXCIX). Однако, мы можем писать и большие цифры, просто необходимо провести верхнюю линию над цифрами, для умножения их на 1000.
К примеру, римское обозначения числа 5000 (5*1000) записывается как
1 миллион (1000*1000) записывается как
Соответственно, 1 550 000 записывается как
Как видим, всё довольно просто.
Таблица римских цифр от одного до тысячи
Ниже я вставил таблицу арабских (русских) цифр начиная от 1 до 1000 и соответствующие им римские цифры.
Римские цифры
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этрусская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Римские цифры — цифры, использовавшиеся древними римлянами в своей непозиционной системе счисления.
Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.
Римские цифры появились за 500 лет до нашей эры у этрусков.
Содержание
Цифры
| 1 | I | лат. unus |
| 5 | V | лат. quinque |
| 10 | X | лат. decem |
| 50 | L | лат. quinquaginta |
| 100 | C | лат. centum |
| 500 | D | лат. quingenti |
| 1000 | M | лат. mille |
В русском языке для закрепления в памяти буквенных обозначений цифр в порядке убывания существуют мнемонические правила:
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
Соответственно M, D, C, L, X, V, I
Примеры
| Число | Римское обозначение | Примечание |
|---|---|---|
| 0 | — | |
| 4 | IV | до XIX века — IIII |
| 8 | VIII | |
| 9 | IX | |
| 31 | XXXI | |
| 46 | XLVI | |
| 99 | XCIX | |
| 583 | DLXXXIII | |
| 888 | DCCCLXXXVIII | от 1 до 1000 — самое длинное |
| 1668 | MDCLXVIII | |
| 1989 | MCMLXXXIX | |
| 2010 | MMX | |
| 2011 | MMXI | |
| 2012 | MMXII | |
| 3999 | MMMCMXCIX | |
| 5000 | ↁ | |
| 10 000 | ↂ |
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трёх раз; таким образом, с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX). В ранние периоды существовали знаки для обозначения бо́льших цифр — 5000, 10 000, 50 000 и 100 000 [источник не указан 683 дня] (тогда максимальное число по упомянутому правилу равно 399 999). При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается как CCLXXXIII, то есть 100+100+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза.
Пример: число 1988. Одна тысяча M, девять сотен CM, восемь десятков LXXX, восемь единиц VIII. Запишем их вместе: MCMLXXXVIII.
Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII».
Меньшая цифра может быть записана и слева от большей, тогда её следует вычесть из большей. В этом случае повторения меньшей цифры не допускаются. По-римски число 94 будет XCIV=100-10+5-1=94 — так называемое «правило вычитания» (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 — как XXXX). Существует шесть вариантов использования «правила вычитания»:
Необходимо отметить, что другие способы «вычитания» не допустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел: например, в программе Microsoft Excel при преобразовании арабских цифр в римские при помощи функции «РИМСКОЕ()» можно использовать несколько видов представления чисел, от классического до сильно упрощенного (так, число 499 может быть записано как CDXCIX, LDVLIV, XDIX, VDIV или ID). Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:
С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Например, число 123123 будет выглядеть так:
Применение
В русском языке римские цифры используются в следующих случаях:
Римские цифры широко употреблялись в СССР при указании даты для обозначения месяца года: 11/III-85 или 9.XI.89. Для указания дат жизни и смерти на надгробиях часто использовался особый формат, где месяц года также обозначался римскими цифрами. С переходом на компьютерную обработку информации форматы даты, основанные на римских цифрах, практически вышли из употребления.
В других языках сфера применения римских цифр может иметь особенности, например, в западных странах римскими цифрами иногда записывается номер года.
Если разложить цифры графически, то получается следующее:
| № | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | X | I | I | I | I | V | I | I | I | I | L | I | I | I | I | V | I | I | I | I | X |
| 1 | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | I | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | V | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | V | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | V | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | I | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | X | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | X | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | X | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | X | I | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | X | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | X | V | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | X | V | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | X | V | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | X | I | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | X | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | X | X | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | X | X | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | X | X | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | X | X | I | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | X | X | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | X | X | V | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | X | X | V | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | X | X | V | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | X | X | I | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | X | X | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | X | X | X | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | X | X | X | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | X | X | X | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | X | X | X | I | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | X | X | X | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | X | X | X | V | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | X | X | X | V | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | X | X | X | V | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | X | X | X | I | X | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | X | L | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | X | L | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | X | L | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | X | L | I | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | X | L | I | V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | X | L | V | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | X | L | V | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | X | L | V | I | I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | X | L | V | I | I | I | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | X | L | I | X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | L | и т. д. до MMMCMXCIX (3999) |
Юникод
| Код | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение [4] | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 50 | 100 | 500 | 1 000 |
| U+2160 | Ⅰ 2160 | Ⅱ 2161 | Ⅲ 2162 | Ⅳ 2163 | Ⅴ 2164 | Ⅵ 2165 | Ⅶ 2166 | Ⅷ 2167 | Ⅸ 2168 | Ⅹ 2169 | Ⅺ 216A | Ⅻ 216B | Ⅼ 216C | Ⅽ 216D | Ⅾ 216E | Ⅿ 216F |
| U+2170 | ⅰ 2170 | ⅱ 2171 | ⅲ 2172 | ⅳ 2173 | ⅴ 2174 | ⅵ 2175 | ⅶ 2176 | ⅷ 2177 | ⅸ 2178 | ⅹ 2179 | ⅺ 217A | ⅻ 217B | ⅼ 217C | ⅽ 217D | ⅾ 217E | ⅿ 217F |
| Значение | 1 000 | 5 000 | 10 000 | — | — | 6 | 50 | 50 000 | 100 000 | |||||||
| U+2160! U+2180 | ↀ 2180 | ↁ 2181 | ↂ 2182 | Ↄ | ↄ | ↄ | ↄ | ↄ | ↄ | |||||||
Отображение всех этих символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.
Регулярные выражения
Регулярное выражение для проверки римских цифр — ‘^(?i)M<0,3>(D?C<0,3>|C[DM])(L?X<0,3>|X[LC])(V?I<0,3>|I[VX])$’. В языке Perl для поиска римских цифр в строке можно использовать регулярное выражение ‘m/((?i)M<0,3>(D?C<0,3>|C[DM])(L?X<0,3>|X[LC])(I[VX]|V?I<0,3>))/g’.
Теперь вы знаете какие однокоренные слова подходят к слову Миллиард римскими цифрами как пишется, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову "Миллиард римскими цифрами как пишется", предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.