Как вводить логарифмы в Wolfram | Alpha?
Иногда трудно ввести его, если логарифм не натуральный, а основание не равно 10, особенно если основание переменное. Итак, кто-нибудь знает правила набора текста?
Я только что проверил два способа:
Вы также можете использовать log_ (b) (a), где b — основание.
Вы также можете использовать log_ (b) (a), где b — основание.
В своей справке Wolfram | Alpha заявляет следующее:
Ответ Майкла заявляет об этом в скобках. Обратите внимание, что скобки определены формально, а скобки — выведены. На самом деле это не имеет значения, но из соображений педантизма.
Справочник по Wolfram | Alpha дает прекрасное понимание этого типа вопросов.
В своей справке Wolfram | Alpha заявляет следующее:
В ответе Майкла это указано в скобках. Обратите внимание, что скобки определены формально, а скобки — выведены. На самом деле это не имеет значения, но из соображений педантизма.
Справочник по Wolfram | Alpha дает прекрасное понимание этого типа вопросов.
Вы можете ввести loga (b). Это дает логарифм b по основанию a
Вы можете ввести loga (b). Это дает логарифм b по основанию a
Сочетания клавиш: введите математические выражения
Вы можете использовать сочетания клавиш для ввода следующих форматов, греческих букв, символов и специальных функций для математических выражений, независимо от того, отвечаете ли вы на компьютере, планшете или смартфоне. Сочетания клавиш для инженерии
Пользователи планшетов и смартфонов: Коснитесь поля ответа, чтобы под ним появилась панель инструментов.
| Для этого математического формата | Введите это с клавиатуры | На планшете или смартфоне откройте … |
|---|---|---|
| ^ |  Цифровая клавиатура для ввода ^ | |
 Буквенная клавиатура для ввода | ||
| . |  Цифровая клавиатура для ввода | |
| () | ( и ) |  Цифровая клавиатура для ввода ( и |
| [] | [ и |  Цифровая клавиатура для ввода [ и |
| <> | <и |  Цифровая клавиатура для ввода <и > |
| + | + |  Цифровая клавиатура для ввода + |
| — (дефис) |  Цифровая клавиатура для ввода | |
 (точка умножения) | * (звездочка) |  Цифровая клавиатура для ввода * |
| sqrt |  Буквенная клавиатура для ввода | |
| nrt |  Клавиатура с буквами для ввода | |
| | x | ( абсолютное значение) | | |  Цифровая клавиатура для ввода |
| vec |  Буквы клавиатуры к введите | |
| hat |  Буквенная клавиатура для ввода hat |
* Чтобы ввести выражение с умножением в числителе: Выберите 
Использовать радианы для аргументов тригонометрических функций, если не запрашивается ответ в градусах.
Чтобы переместить курсор в ответ: На компьютере используйте клавиши со стрелками на клавиатуре (




Выберите 

Выберите 
Тема будет напечатана в том виде, в котором она отображается в Интернете. Чтобы распечатать всю тему, выберите 
gives the natural logarithm of z (logarithm to base 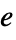
Details
Examples
Basic Examples (6)
Log gives the natural logarithm (to base 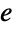
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion shifted from the origin:
Asymptotic expansion at a singular point:
Scope (51)
Numerical Evaluation (7)
Evaluate numerically to high precision:
The precision of the output tracks the precision of the input:
Evaluate Log efficiently at high precision:
Log can deal with real ‐ valued intervals:
Log threads elementwise over lists and matrices:
It threads over lists in either argument:
Log can be used with CenteredInterval objects:
Specific Values (5)
Simple exact values are generated automatically:
Values at infinity:
Zero argument gives a symbolic result:
Find a value of x for which the Log [ x ] =0.5 :
Visualization (3)
Plot the Log function:
Plot the real part of 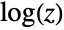
Plot the imaginary part of 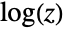
Polar plot with 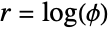
Function Properties (12)
Log [ z ] gives the logarithm with base E :
Log is defined for all real positive values:
Log achieves all real values:
The range for complex values:
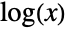
Nor is it meromorphic:
The issue is a branch cut along the negative real axis:
The branch cut exists for any fixed value of 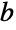
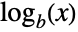
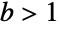
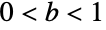
Log is neither non-negative nor non-positive:
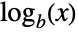
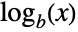
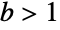
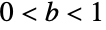
Differentiation (5)
The first derivative with respect to z :
The first derivative with respect to b :
Formula for the 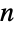
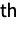
Derivative of a nested logarithmic function:
Integration (3)
Indefinite integrals of Log :
Definite integral of Log :
Series Expansions (5)
Taylor expansion for Log :
Plot the first three approximations for Log around 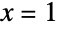
General term in the series expansion of Log around 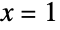
Asymptotic expansions at the branch cut:
The first term in the Fourier series of Log :
Log can be applied to power series:
Function Identities and Simplifications (6)
Basic identity for Log :
Logarithm of a power function simplification:
Simplify logarithms with assumptions:
Logarithm of a product:
Expand assuming real variables x and y :
Function Representations (5)
Log arises from the power function in a limit:
Log can be represented in terms of MeijerG :
Log can be represented as a DifferentialRoot :
Generalizations & Extensions (2)
Log can deal with real ‐ valued intervals from 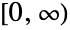
Log is a numerical function:
Applications (8)
Plot Log for various bases:
Plot the real and imaginary parts of Log :
Plot the real and imaginary parts over the complex plane:
Plot data logarithmically and doubly logarithmically:
Benford’s law predicts that the probability of the first digit is 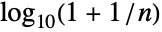
Analyze the first digits of the following sequence:
Use Tally to count occurrences of each digit:
Shannon entropy for a set of probabilities:
Equi ‐ entropy surfaces for four symbols:
Approximate the 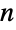
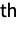
Exponential divergence of two nearby trajectories for a quadratic map:
Properties & Relations (13)
Compositions with the inverse function might need PowerExpand :
Get expansion that is correct for all complex arguments:
Simplify logarithms with assumptions:
Convert inverse trigonometric and hyperbolic functions into logarithms:
Log arises from the power function in a limit:
Solve a logarithmic equation:
Reduce a logarithmic equation:
Numerically find a root of a transcendental equation:
The natural logarithms of integers are transcendental:
Solve differential equations:
Log is automatically returned as a special case for various special functions:
Possible Issues (7)
For a symbolic base, the base b log evaluates to a quotient of logarithms:
Generically, 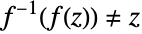
Because intermediate results can be complex, approximate zeros can appear:
Machine-precision inputs can give numerically wrong answers on branch cuts:
Use arbitrary ‐ precision arithmetic to obtain correct results:
Compositions of logarithms can give functions that are zero almost everywhere:
This function is a differential-algebraic constant:
Logarithmic branch cuts can occur without their corresponding branch point:
The argument of the logarithm never vanishes:
But it can take negative values, so the logarithm has a branch cut:
The kink at 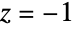
Logarithmic terms in Puiseux series are considered coefficients inside SeriesData :
In traditional form, parentheses are needed around the argument:
Neat Examples (6)
Successive integrals of the log function:
Plot the Riemann surface of Log :
Plot Log at integer points:
Calculate Log through an analytically continued summed Taylor series:
Visualize how the value is approached as 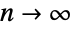
Plot the Riemann surface of Log [ Log [ z ] ] :
Как в вольфрам альфа написать логарифм
Решение уравнений
Чтобы получить решение уравнения вида 
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
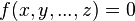

Решение неравенств
Решение в Wolfram Alpha неравенств типа 0″ src=»http://upload.wikimedia.org/math/3/d/9/3d97eb56e02c2889dd20a89529548180.png»/>, 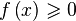

Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


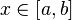


Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],
Для того, чтобы построить график функции 
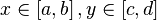


Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
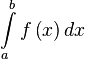
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать:
Ошибки при работе с системой
Например, разложить на слагаемые
Partial fraction expansion(1-x^2)/(x^3+x)
используются формулы разложения функций в ряд Тейлора (Taylor series) и ряд Маклорена (Maclaurin series) или
Series expansion at x=0
Разложить в ряд Лорана:
Laurent expansion z*cos(1/z) at z =0
Найти вычет функции в точке:
residue of (e^(1/(1-z^2 ))/((1-e^z )* sin(z^2 ) )) at point z = 0
Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Комплексно сопряженное z*

