Равнобедренный треугольник — свойства, признаки и формулы
Общие сведения
Замкнутую фигуру, состоящую из трёх пересекающихся прямых и такого же количества внутренних углов, называют треугольником. Отрезки, которые соединяют точки, образующие фигуру, называют сторонами. Для обозначения используют малые латинские буквы. Точка, в которой соединяется 2 стороны, называется вершиной. Её принято подписывать заглавными буквами, например, A, B, C.
Существует несколько видов фигур по типу углов и по длинам сторон:

Отличительная черта фигуры — сумма углов равняется 180 градусов. Это один из самых важных признаков, позволяющих отнести многоугольник к треугольникам. Причём каждая такая фигура имеет замечательные линии и точки.
Прежде всего это медиана — отрезок, построенный из вершины к центру противолежащей стороны, разделяющий фигуру на 2 равных треугольника. Биссектрисой называют линию, построенную к противоположной стороне и разделяющую угол на 2 равные части. Также можно опустить перпендикуляр на любую сторону из вершины. Называют такую линию высотой.
В треугольнике можно провести по 3 любых таких линии. Причём точка пересечения отрезков имеет своё название: 3 высоты встречаются в ортоцентре, а биссектрисы — инцентре. Если в треугольник вписать окружность, её центр совпадёт с местом пересечения медиан. Эта точка является центроидом, центром массы фигуры. Кроме этого, можно описать круг, в центре которого будут пересекаться серединные перпендикуляры.
Признаки равнобедренной фигуры
Существует 4 явления, с помощью которых можно определить принадлежность тела к треугольникам. Все они сгруппированы в 3 теоремы:

Для доказательства первой теоремы нужно использовать признаки равенства треугольников. Если изобразить на чертеже фигуру ABC и из вершины B построить высоту, согласно заданным данным, она будет медианой или биссектрисой. В первом случае противоположная сторона будет разделена на 2 равные части AD и DC. Значит, треугольники ABD и DBC одинаковые. Отсюда следует, что у фигур есть равные стороны: AB = BC., то есть боковые грани имеют одинаковую длину, что и требуется по определению.
В случае с биссектрисой ход рассуждений будет такой же. Отличие заключается лишь в том, что используется второй признак равенства: если грань и 2 прилежащих к ней угла одного треугольника совпадают со стороной и двумя прилежащими к ней углам другого, они равны.
Доказательство второй теоремы следует построить на нахождении равных сторон. Для этого нужно отложить серединный перпендикуляр a и доказать, что линия будет проходить через вершину B. Если она не будет пересекать угол B, она касается AB или BC. Пусть точкой пересечения перпендикуляра будет M. Тогда по первому признаку AKM = CKM, значит, углы MCK и MAK также равны. По условию теоремы MCK = MAB → MAK = MAB, что противоречит аксиоме измерения углов. Отсюда можно утверждать, что серединный перпендикуляр не пересекает BC или AC. Значит, прямая проходит через вершину B.
Третью теорему легко можно доказать, отложив на луче BM равный ему по длине отрезок. Затем, соединив A и D, построить треугольник ADM. Углы ABM и ADM одинаковые. Отсюда AB = AD → AB = BC, что и требовалось доказать.

Свойства треугольника
Равнобедренный треугольник относится к особому виду многоугольника. Равные его стороны называют боковыми, а отличную от них — основанием. Любую фигуру можно охарактеризовать с помощью свойств.
Признаки позволяют определить, является ли фигура равнобедренной. Из сформулированной второй теоремы следует: каждая точка, лежащая на серединном перпендикуляре, будет равноудалённой от концов боковых отрезков. Из основных свойств равнобедренного треугольника можно выделить:

А также из равенства треугольников следует, что ADB = CDB, а вершина ADC — развёрнутая. Её величина равна 1800. Значения углов, на которые она разбивается лучом DB, будет составлять 900. Таким образом, ADB = CDB = 900. Отрезок D перпендикулярен AC.
Из последнего свойства следует, что медиана является биссектрисой и высотой. Находящиеся при основании углы в равнобедренном треугольнике можно вычислить по формуле: ACB = BCA = 900 — CAB/2, где CAB — вершина, расположенная напротив основания.
Из указанных свойств следует, что точка пересечения любых замечательных линий одновременно является ортоцентром, инцентром и центром тяжести фигуры. Это важное замечание, позволяющее вычислять параметры с помощью окружности, описываемой вокруг треугольника.
Формулы и пример задания
Правильный треугольник, где все 3 стороны равны, является частным случаем равнобедренного, поэтому все формулы для поиска параметров будут одинаковыми. Самым часто используемым выражением, применяемым на уроках, является формула для поиска площади: S = (b * h)/2, где: b – основание, h – высота. Существует и более сложное равенство, позволяющее определить S, зная размеры двух прилежащих сторон: S = (b * √(a2 – (b2 / 4)) / 2.
Кроме поиска площади фигуры, в треугольнике можно вычислить:

Формулы, признаки и свойства равнобедренного треугольника важны для геометрии. Используя их, можно решать сложные задачи, связанные с многогранниками различных видов.
Пусть имеется равнобедренный треугольник ABC, в котором построена медиана BM. Известно, что периметр всего многоугольника 32, а фигуры ABM — 24. Нужно вычислить длину высоты. Следует понимать, что в равнобедренной фигуре медиана является высотой и биссектрисой. Сторону AB можно принять за X. Соответственно, противоположная сторона BC будет тоже равняться X. Из свойств треугольника AC разделяется в точке M на 2 одинаковых отрезка. Пусть каждый из них будет равняться Y.
По условию периметр ABC = 32, значит: 2x + 2 y = 32. Обе части равенства можно разделить на 2. В результате получится, что сумма AB и AM составляет 16. Так как периметр треугольника ABM=24, то BM = P – 16 = 24 – 16 = 8. Задача решена: длина высоты, построенная в ABC, будет равняться 8.
Геометрия. 7 класс
Равнобедренный треугольник
Геометрические термины
Медиана
Равнобедренные треугольники
Элементы равнобедренного треугольника
Построение равностороннего треугольника
Необходимо запомнить
AB и BC – боковые стороны треугольника ∆ABC.
AC – основание треугольника ∆ABC.
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
AF – высота, медиана, биссектриса ∆ABC.
Задача на доказательство
Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана равнобедренного треугольника».
На рисунке изображён треугольник ABC, при этом AM – медиана, AM = BM. Докажем, что угол А равен сумме двух других углов ∆ABC.
По условию AМ = ВМ → ∆АВМ – равнобедренный (по определению равнобедренного треугольника) → ∠МВА = ∠ВАМ (по свойству равнобедренного треугольника).
Т. к. АМ – медиана ∆ABC и AМ = ВМ → AМ = ВМ = СМ → ∆АМС – равнобедренный (по определению равнобедренного треугольника)=> ∠МСА = ∠MАС (по свойству равнобедренного треугольника).
Получаем, что ∠А = ∠MАС + ∠ВАМ = ∠МВА + ∠МСА = ∠В + ∠С.
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Равнобедренный треугольник – треугольник, у которого две стороны равны.
Равносторонний треугольник – треугольник, у которого все стороны равны.
Любой равносторонний треугольник является равнобедренным, обратное не верно.
Теоретический материал для самостоятельного изучения.
Вы уже познакомились с такими понятиями как треугольник, рассмотрели его виды.
Рассмотрим такие виды треугольников: как равнобедренные и равносторонние, более подробно. Начнём с описания равнобедренного треугольника. Но для начала, дадим ему определение.
Треугольник называется равнобедренным, если две его стороны равны.
В равнобедренном треугольнике равные стороны называются боковыми, а третья сторона – основанием.
AB и BC – боковые стороны ∆ABC.
Если третья сторона равна двум другим, то любая сторона может быть основанием.
Теперь рассмотрим треугольник, у которого все стороны равны. Такой треугольник называется равносторонним.
Докажем две теоремы о свойствах равнобедренного треугольника.
Теорема: В равнобедренном треугольнике углы при основании равны.
Теперь сформулируем теорему о биссектрисе, медиане и высоте равнобедренного треугольника, проведённых к основанию.
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой треугольника.
AF– биссектриса ΔABC
Доказать: AF – медиана и высота.
Справедливы и следующие утверждения.
Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
А медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.
AF – медиана ∠ВАС ΔABC
Доказать: AF – биссектриса и высота ΔABC.
∆ABF = ∆ACF т. к. ∠В = ∠С (по свойству равнобедренного треугольника); BF = CF (по определению медианы треугольника); AB = AC (∆ABC – по определению равнобедренного треугольника) → ∠BАF = ∠FАC (как соответствующие элементы равных треугольников) => AF ‑ биссектриса ΔABC (по определению биссектрисы треугольника).
∠AFB = ∠AFC как соответствующие элементы равных треугольников, но их сумма равна 180 (по свойству развернутого угла).
∠AFB = ∠AFC = 90° →AF – высота треугольника (по определению высоты треугольника).
Сегодня мы узнали, что такое равнобедренный, равносторонний треугольник, рассмотрели свойства равнобедренного треугольника.
Разберем задачу на доказательство.
Рассмотрим, как можно решить задачу на доказательство, используя понятие: «медиана равнобедренного треугольника».
На рисунке изображён треугольник ABC, при этом AM – медиана, при этом AM = BM. Докажем, что угол А равен сумме двух других углов ∆ABC.
По условию AМ = ВМ → ∆АВМ – равнобедренный (по определению равнобедренного треугольника)→ ∠МВА = ∠ВАМ (по свойству равнобедренного треугольника).
Т. к. АМ – медиана ∆ABC и AМ = ВМ → AМ = ВМ = СМ → ∆АМС – равнобедренный (по определению равнобедренного треугольника) → ∠МСА = ∠ВАС (по свойству равнобедренного треугольника).
Получаем, что ∠А = ∠ВАС + ∠ВАМ = ∠МВА + ∠МСА = ∠В + ∠С.
Что и требовалось доказать.
Разбор решения заданий тренировочного модуля.
Периметр равнобедренного треугольника ABC равен 50 см, боковая сторона AC на 4 см больше основания BC. Найдите основание треугольника.
Решение: Пусть х – основание ВС треугольника АВС, тогда АС = АВ (как боковые стороны равнобедренного треугольника).
АС = АВ = х + 4 (по условию).
Периметр треугольника АВС равен сумме всех его сторон, т. е. 50 см = АС + ВС + АВ,
х = 14 см – основание BC.
На рисунке изображён равнобедренный треугольник ABC. AC – основание треугольника, ∠1 = 120. Найдите ∠2.
Решение: ∠1 и ∠АСВ – смежные →∠1 + ∠АСВ = 180, значит:
АВС – равнобедренный, значит: ∠ВАС = ∠АСВ = 60 (углы при основании равнобедренного треугольника равны).
Равнобедренные треугольники
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Равнобедренный треугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
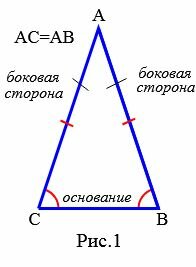
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (\( \small \angle A \) ) называется вершинным углом. Углы между основанием и боковыми сторонами (\( \small \angle B, \ \angle C \) ) называются углами при основании.
 |
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
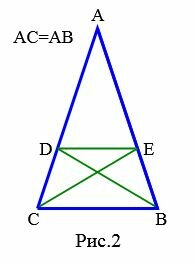 |
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что \( \small \angle B= \angle C. \) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол \( \small \angle A \) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
Из \( \small AB=AC\) и \( \small AD=AE \) следует:
Из (2) и (4) следует, что \( \small \angle B= \angle C. \)
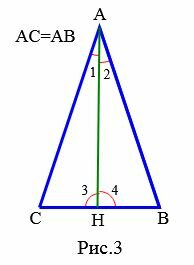 |
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису \( \small AH \) треугольника. Тогда \( \small \angle CAH=\angle BAH. \) Докажем, что \( \small \angle B= \angle C. \) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle CAH=\angle BAH. \) Отсюда следует: \( \small \angle B= \angle C. \)
Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.
Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle 1=\angle 2. \) Тогда \( \small CH=HB, \) \( \small \angle 3=\angle 4. \) Равенство \( \small CH=HB \) означает, что \( \small AH \) является также медианой треугольника ABC. Углы \( \small \angle 3\) и \( \angle 4 \) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда \( \small AH \) является также высотой треугольника \( \small ABC. \) Поскольку высота \( \small AH \) перпендикулярна к \( \small BC \) и \( \small CH=HB, \) то \( \small AH \) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
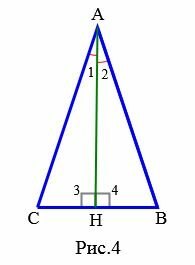
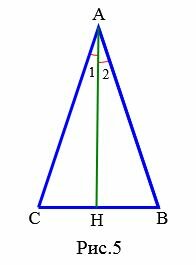
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (первый признак равенства треугольников): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
  |
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда
Применим теорему синусов для треугольника \( \small AHC \):
Применим теорему синусов для треугольника \( \small AHB \):
тогда, из (5), (6), (7) получим:
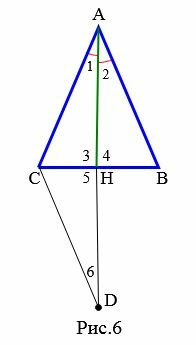 |
Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.
1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Задачи и решения
Задача 1. Известны основание \( \small a=5 \) и высота \( \small h=6 \) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
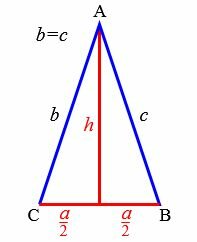 |
Решение. Найдем боковые стороны \( \small b \) и \( \small c \) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
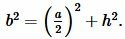 |
Подставляя значения \( \small a \) и \( \small h \) в (9), получим:
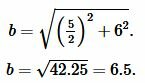 |
Боковая сторона \( \small c \) равнобедренного треугольника равна:
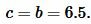 |
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
Подставляя значения \( \small a=5, \) \( \small b=6.5 \) и \( \small c=6.5 \) в (10), получим:
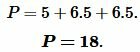 |
Найдем угол \( \small B \) равнобедренного треугольника:
Подставляя значения \( \small a=5, \) \( \small h=6 \) в (11), получим:
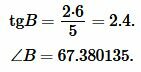 |
Тогда угол \( \small C \) равнобедренного треугольника равен:
 |
Поскольку сумма всех углов треугольника равна 180°, то имеем:
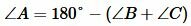 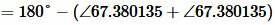 , , |
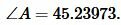 |
Площадь треугольника можно вычислить из формулы:
Подставляя значения \( \small a=5, \) \( \small h=6 \) в (12), получим:















