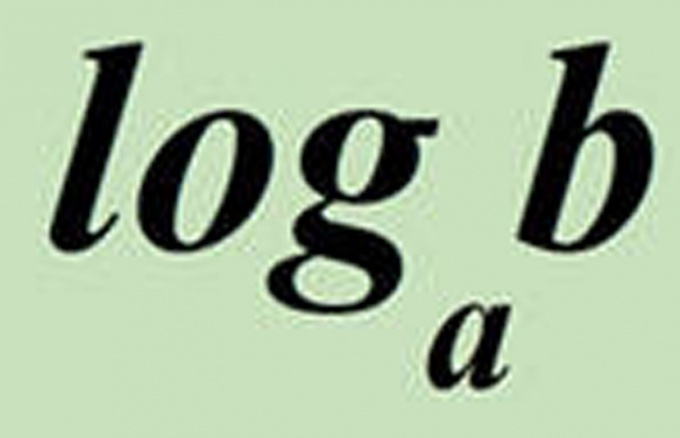Слово Как в калькуляторе написать логарифм по основанию - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Десятичный логарифм

Определение. Десятичный логарифм — логарифм по основанию 10.

Калькулятор десятичных логарифмов

Свойства десятичного логарифмов

lg( x · y ) = lg x + lg y

lg 100 = lg 10 2 = 2

lg 1000 = lg 10 3 = 3

Запишем очевидное равенство:

lg b · lg a = lg a · lg ab

Возведем 10 в соответствующие степени

10 lg b · lg a = 10 lg a · lg b

(10 lg b ) lg a = (10 lg a ) lg b

Используем формулы логарифма произведения и степени получим:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b ;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c ;

Вычислить log₉ 5 · log₂₅ 27.

Перейдем к основе 10:

log₉ 5 · log₂₅ 27 = lg 5 lg 9 · lg 27 lg 25

Используем свойство логарифма степени lg x n = n lg x :

lg 5 lg 9 · lg 27 lg 25 = lg 5 lg 3 2 · lg 3 3 lg 5 2 = lg 5 2 lg 3 · 3 lg 3 2 lg 5 = 3 4

Перейдем к основе 10:

log ₃₀ 8 = lg 8 lg 30 = lg 2 3 lg (3 · 10) =

Используем свойство логарифма степени, произведения, частного и то что 2= 10 5 :

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Как посчитать логарифм на калькуляторе?

Как посчитать логарифм на калькуляторе?

В категории Естественные науки Спросил Malanrad

1 Ответ 2386 Просмотров 1 месяц назад

Для добавления вопроса на сайт, блог или форум просто скопируйте и вставьте в html код:

Для того, чтобы посчитать логарифм на калькуляторе, для этого на этом калькуляторе должны присутствовать кнопки «log» и «ln».

Для начала нужно узнать, что же такое логарифм.

Логарифм, это показатель степени, в которую нужно возвести основание.

Чтобы вам было это более понятным, можно сформулировать так, что нужно возвести основание в определённую степень.

Например, вы хотите получить логарифм.

В компьютере это делается следующим образом:

2^10 и нажимаем Enter. Получаем сумму одна тысяча двадцать четыре.

Но это получается сумма, возведённая в степень.

А вот чтобы получить логарифм, нужно понять, сколько раз нужно двойку умножить на саму себя, чтобы получить число одна тысяча двадцать четыре.

Сама формула 2^10 говорит о том, что из числа одна тысяча двадцать четыре, логарифмом будет число десять.

Для того, чтобы считать логарифмы на калькуляторе, следует сделать следующее:

1. Идёте в магазин и покупаете калькулятор.

2. Когда покупаете калькулятор, проследите, чтобы были клавиши, которые имеют две кнопки: «log» и «ln». Это должен быть инженерный калькулятор.

Понятно, что считать в магазине вы не будете.

3. Приходите домой и берёте в руки калькулятор.

4. Включаете его, и набираете то число, из которого вы хотите получить логарифм.

Если хотите получить натуральный логарифм, то нужно после набора числа нажать кнопку «ln». Сокращённое название этой кнопки и будет показателем, как натуральный логарифм. Если же нужно получить десятичный логарифм, тогда нажимается кнопка с надписью «log».

Вот таковым образом и можно посчитать логарифм на калькуляторе.

но согласитесь, что прежде, чем считать на калькуляторе, нужно хоть немного иметь представление о том, что такое логарифм, ибо, если этого не знать, то можно просто тупо жать на кнопки, но толку от этого не будет никакого.

Источник

Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов

Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.

Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.

В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.

Итак, давайте разбираться, что такое логарифм.

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Основные свойства логарифмов

Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:

Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!

Рассмотрим свойства логарифмов на примерах.

Логарифмический ноль и логарифмическая единица

Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.

Запомните, что логарифм от a по основанию а всегда равен единице:

log_a a = 1 – это логарифмическая единица.

Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:

log_a 1 = 0 – логарифмический ноль.

Основное логарифмическое тождество

В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.

Вторая формула по сути является просто переформулированным определением логарифма

Разберем применение тождества на примере:

Необходимо найти значение выраженияСначала преобразуем логарифм

Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:

10 примеров логарифмов с решением

1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник

Как считать логарифм с калькулятором

Инструкция

Совет 2: Как посчитать в инженерном калькуляторе

Инструкция

ДРУГОЕ

Как решать логарифмы

Логарифм числа b определяет показатель степени для возведения исходного положительного числа a, являющегося основанием…

Как посчитать проценты на калькуляторе

Высчитывать проценты приходится часто. Например, чтобы определить переплату по кредиту или посчитать пеню за просрочку,…

Как найти процент от числа

Одним процентом от числа называют сотую долю этого числа и обозначают 1%. Поэтому 100% этого числа равно самому числу,…

Как вычитать проценты

Как считать сумму

Суммой называют результат сложения. Результатом суммы могут являться не только числа, но и вектора, функции, матрицы и…

Как найти среднее геометрическое чисел

Среднее геометрическое чисел зависит не только от абсолютной величины самих чисел, но и от их количества. Нельзя путать…

Как на калькуляторе посчитать степень

Для возведения числа в степень можно использовать как простейшие, так и научные калькуляторы. Во втором случае…

Как вычислить на калькуляторе логарифм

Как взять логарифм от логарифма

Логарифм используется для нахождения показателя степени, в которую следует возвести основание для получения числа,…

Как найти основание логарифма

Как найти натуральный логарифм

Термин «логарифм» произошел от двух греческих слов, одно из которых обозначает «число», а…

Как найти антилогарифм

Логарифмом (от греч. logos – «слово», «отношение», arithmos – «число») числа b по…

Как вычислить экспоненту

Экспонента – это математическая функция, значение которой вычисляется по формуле «е» в степени…

Как складывать логарифмы

Логарифмом числа b по основанию a называют такую степень x, что при возведении числа a в степень x получается число b:…

Как найти корень степени из числа

Иногда возникают ситуации, когда приходится выполнять какие-либо математические вычисления, в том числе извлекать корни…

Как вычислить десятичный логарифм

Вычисление логарифмов может понадобиться для нахождения значений по формулам, содержащим в качестве неизвестных…

Как посчитать натуральный логарифм

Как посчитать в инженерном калькуляторе

Существует три вида инженерных калькуляторов: с обратной польской, арифметической и формульной записью. Бывают и такие…

Как вычислить натуральный логарифм

Логарифмы используются при решении тех уравнений в математике и прикладных науках, в которых неизвестные величины…

Как посчитать логарифм на калькуляторе

Логариифм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a, чтобы…

Как определить процент от числа

Источник

Как посчитать логарифм на калькуляторе

Логариифм числа b по основанию a определяется как показатель степени, в которую нужно построить основание a, дабы получить число b. Как водится, современные калькуляторы дозволяют посчитать логарифмы по основанию 10 и е, то есть десятичный (log) и настоящий (ln) логарифмы соответственно.

Вам понадобится

Инструкция

3. После этого нажмите на кнопку “log”, если хотите обнаружить десятичный логарифм либо на кнопку “ln” – если естественный. Позже этого калькулятор произведет расчет и на экране высветится результат. В примере с числом 324, если посчитать десятичный логарифм, получится результат 2.5104, а если естественный, то 5.7807.

Совет 2: Как посчитать степень числа

Степень числа разбирают в школе на уроках алгебры. В жизни такая операция выполняется редко. Скажем, при расчете площади квадрата либо объёма куба применяются степени, так как длина, ширина, а для куба и высота – равные величины. В остальном возведение в степень почаще каждого носит прикладной производственный нрав.

Вам понадобится

Инструкция

1. Посчитать степень числа на математическом языке обозначает построить всякое число в какую-либо степень. Представим, нужно число Х построить в степень n.Для этого число Х умножается само на себя n раз.

2. Пускай Х = 125, а степень числа, т. е. n = 3. Это обозначает, что число 125 необходимо умножить само на себя 3 раза.125^3 = 125*125*125 = 1 953 125Ещё пример.3^4 = 3*3*3*3 = 81

3. При работе с негативным числом надобно быть опрятным со знаками. Следует помнить, что четная степень (n) даст знак плюс, нечетная – знак минус.Скажем(-7)^2 = (-7)*(-7) = 49(-7)^3 = (-7)*(-7)*(-7) = 343

4. Нулевая степень (n = 0) от всякого числа неизменно будет равна единице.15^0 = 1(-6)^0 = 1(1/3)^0 = 1Если n = 1, число умножать само на себя не нужно.Будет7^1 = 7329^1 = 329

5. Операция, обратная возведению числа в степень, именуется извлечение корня.Если 5^2 = 25, то квадратный корень из 25 будет равен 5.Если 5^3 = 125, то корень третей степени равен 5.Если 8^4= 4 096, то корень четвертой степени из 4 096 будет равен 8.

6. Если n = 2, тогда степень называют квадратом, если n = 3, степень называют кубом. Вычисление квадрата и куба из чисел первого десятка изготавливать довольно легко. Но с увеличением числа, возводимого в степень, и с увеличением самой степени, вычисления становятся трудоемкими. Для таких вычислении были разработаны особые таблицы. Также существуют особые инженерные и online калькуляторы, программные продукты. В качестве простейшего программного продукта для операций со степенями дозволено применять табличный редактор Excel.

Совет 3: Как посчитать в инженерном калькуляторе

Существует три вида инженерных калькуляторов: с обратной польской, арифметической и формульной записью. Бывают и такие калькуляторы, которые поддерживают переключения способов ввода выражений. Применение всякого из них имеет свои особенности.

Инструкция

1. Определите, какой способ ввода поддерживает ваш калькулятор. Если на нем отсутствует клавиша со знаком равенства, но есть клавиша со стрелкой, направленной вверх, перед вами – машинка с обратной польской записью. Присутствие клавиши со знаком равенства говорит о том, что в приборе применяется арифметический способ ввода. Наконец, если индикатор калькулятора, помимо сегментных знакомест, имеет еще и матричные, то агрегат рассчитан на формульную запись. В последнем случае, взамен знака равенства на соответствующей клавише может быть нанесено слово “EXE” либо “Enter”.

2. Дабы произвести расчет на калькуляторе с обратной польской записью, нужно сначала определить очередность выполнения действий. Делается это по общепризнанным математическим правилам.Действия с двумя операндами исполняйте дальнейшим образом. Введите 1-й операнд. Нажмите кнопку со стрелкой вверх, дабы перенести его на один регистр стека вверх. Введите 2-й операнд, и лишь позже этого нажмите на клавишу математического действия. На индикаторе отобразится итог вычисления.Для выполнения действия с одним операндом легко введите его, а после этого нажмите на соответствующую этому действию кнопку.

3. На калькуляторе с арифметической записью действия с двумя операндами исполняйте так же, как на обыкновенном калькуляторе. Действия же с одним операндом исполняйте так же, как на машинке с обратной польской записью.Если на клавиатуре присутствуют клавиши со скобками, надобность в определении очередности вычислений отсутствует. Следует, впрочем, не допускать превышения яруса вложенности скобок, указанного в инструкции. При отсутствии инструкции определить данный ярус дозволено опытным путем, нажав клавишу с открывающей скобкой несколько раз и подметив, позже которого по счету нажатия появилось сообщение об ошибке.

4. В калькулятор с формульной записью выражение вводят так же, как оно записывается на бумаге. Если поле ввода однострочное, формулы, содержащие дроби, преобразовывают в «одноэтажные» с поддержкой скобок и знака деления. При необходимости, введенное выражение дозволено скорректировать, пользуясь клавишами с горизонтальными стрелками, а также кнопками “Insert”, “Backspace” и “Delete” (на различных калькуляторах их наименования могут различаться). После этого нажимают клавишу “EXE” либо “Enter” и получают итог. Если данный итог требуется разместить в следующую формулу, пользуются клавишей “ANS”.

5. Во многих калькуляторах некоторые из клавиш способны исполнять больше одной функции. Примитивное нажатие клавиши соответствует выполнению той операции, наименование которой указано прямо на ней. Другие операции обозначены рядом с кнопкой тем либо другим цветом. Дабы принудить калькулятор исполнить такую функцию, следует вначале нажать регистровую клавишу, имеющую тот же цвет (она может именоваться “F”, “2ndF”, “S”), а после этого – кнопку, рядом с которой указана надобная вам операция.

Видео по теме

Совет 4: Как посчитать настоящий логарифм

Из всеобщего ряда логарифмов два выделены особенно – это логарифм по основанию 10 (десятичный) и по основанию, равному числу “e” – константе, которую называют «числом Эйлера». Эта константа является числом иррациональным, то есть не имеет точного значения, а представляет собой безмерную дробь. Логарифм с таким основанием именуется естественным и имеет гораздо большее использование в интегральном и дифференциальном исчислении, чем десятичный логарифм.

Инструкция

1. Используйте онлайн-калькуляторы как особенно стремительный метод вычисления естественных логарифмов при наличии доступа в интернет. Таких сервисов довольно много в сети, но искать их через поисковые системы нет необходимости – некоторые из поисковиков и сами имеют вычислители с надобной функцией. Скажем, дозволено воспользоваться калькуляторами поисковых систем Google либо Nigma. Перейдя на основную страницу всякий из этих систем, введите в поле для поискового запроса запись необходимого вам математического действия. Скажем, для вычисления естественного логарифма числа 0,489 введите «ln 0.489». В качестве разделителя целой и дробной частей класснее применять точку, правда Nigma осознает верно и число с разделителем-запятой.

2. Задействуйте программный калькулятор, встроенный в операционную систему Windows, если доступ в интернет отсутствует. Открыть его дозволено через основное меню на кнопке «Пуск» (раздел «Все программы», подраздел «Типовые», сегмент «Служебные», пункт «Калькулятор») либо с подмогой диалога запуска программ, тот, что вызывается сочетанием клавиш WIN + R. В диалоге нужно ввести команду calc и щелкнуть кнопку «OK».

3. Переключите запущенный калькулятор в больше продвинутый режим. Если вы используете операционную систему Windows XP либо больше раннюю версию, то необходимый режим будет именоваться «инженерный», а в больше поздних версиях (Windows 7 и Windows Vista) – «ученый». Пункт с таким наименованием в всякий версии ОС размещен в раздел «Вид» меню калькулятора.

4. Используйте клавиатуру либо кнопки интерфейса на экране для ввода числа, естественный логарифм которого необходимо вычислить. После этого щелкните кнопку с меткой ln и программа посчитает и покажет итог вычисления.

Совет 5: Как обнаружить логарифм числа

На практике почаще каждого используются десятичные логарифмы, которые принято называть стандартными. Для их нахождения составлены особые таблицы, применяя которые дозволено обнаружить значение логарифма всякого позитивного числа с той либо другой точностью, заблаговременно приведя его к стандартному виду. Для решения большинства задач абсолютно довольны четырехзначные таблицы Брадиса с точностью до 0,0001, которые содержатся мантиссы десятичных логарифмов. Отзыв дозволено легко обнаружить по одному виду числа. Обращение с таблицами крайне примитивное.

Вам понадобится

Инструкция

1. Приведите логарифм к стандартному виду, если его основание не равно 10. Используйте формулу перехода от одного основания к иному.

3. Определите число для нахождения мантиссы как целое. Проигнорируйте в данном числе запятую, если она есть и отбросьте все нули, стоящие в конце числа. Расположение запятой в десятичном числе и последние нули никаким образом не влияют на величину мантиссы. Запишите образовавшееся целое число. Скажем, у логарифма числа 56,3 оно равно 563. В зависимости от того, сколько цифр содержится в этом числе, зависит алгорифм работы с четырехзначными таблицами. Существует три типа алгорифмов.

4. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения является трехзначным. Обнаружьте в четырехзначных математических таблицах Брадиса таблицу XIII «Мантиссы десятичных логарифмов». Перейдите на строчку, содержащую в первом столбце «N» эти две первые цифры числа, по которому ищется мантисса. Скажем, если имеем число 563, то ищите строчку, где в первом столбе стоит 56. После этого продвигайтесь по этой строчке вправо до ее пересечения со столбцом, номер которого совпадает с третьей цифрой начального числа. В нашем примере это столбец с номером 3. На пересечении обнаруженной строки и столбца находится значение мантиссы. Мантисса, обнаруженная по числу 563 равна 0,7505.

5. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения состоит из 2-х либо одной цифры. Припишите мысленно к этому числу такое число нулей, дабы оно стало трехзначным. Если число равно 56, то получается 560. Обнаружьте мантиссу по полученному трехзначному числу. Для этого исполните действия из шага 4. Мантисса по числу 560 равна 0,7482.

6. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения является четырехзначным. Обнаружьте мантиссу для числа, изображенного первыми тремя цифрами данного числа. Для этого исполните действия из шага 4. После этого передвигайтесь по горизонтальной строке от обнаруженной мантиссы в правую часть таблицы, расположенную за вертикальной толстой чертой и содержащей поправки на четвертую цифру. Обнаружьте в области поправок столбец с номером, совпадающим с четвертой цифрой числа. Прибавьте поправку, находящуюся на пересечении строки и столбца, к мантиссе, обнаруженной по трехзначному числу. Скажем, если число для нахождения мантиссы равно 5634, то мантисса по 563 равна 0,7505. Поправка по цифре 4 равна 3. Окончательный итог равен 0,7508.

7. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее содержит больше четырех цифр. Округлите число до четырех знаков так, дабы все цифры, начиная с пятой, были нулями. Отбросьте последние нули и обнаружьте мантиссу по четырехзначному числу. Для этого исполните действия из шага 7.

8. Обнаружьте логарифм числа как сумму колляции и мантиссы. В рассматриваемом примере логарифм числа 56,3 равен 1,7505.
Видео по теме

Совет 6: Как обнаружить логарифм

Логарифмом числа x по основанию a именуется такое число y, что a^y = x. От того что логарифмы облегчают дюже многие фактические вычисления, значимо уметь ими пользоваться.

Инструкция

1. Логарифм числа x по основанию a будем обозначать loga(x). Скажем, log2(8) — логарифм числа 8 по основанию 2. Он равен 3, так как 2^3 = 8.

2. Логарифм определен только для позитивных чисел. Негативные числа и нуль не имеют логарифмов вне зависимости от основания. При этом сам логарифм может быть любым числом.

3. Основанием логарифма может служить всякое правильное число, помимо единицы. Впрочем на практике почаще каждого применяются два основания. Логарифмы по основанию 10 именуются десятичными и обозначаются lg(x). Десятичные логарифмы почаще каждого встречаются в фактических вычислениях.

4. Второе знаменитое основание для логарифмов — иррациональное трансцендентное число e = 2,71828… Логарифм по основанию e именуется естественным и обозначается ln(x). Функции e^x и ln(x) владеют специальными свойствами, значимыми для дифференциального и интегрального исчисления, следственно настоящие логарифмы почаще применяются в математическом обзоре.

5. Логарифм произведения 2-х чисел равен сумме логарифмов этих чисел по тому же основанию: loga(x*y) = loga(x) + loga(y). Скажем, log2(256) = log2(32) + log2(8) = 8.Логарифм частного 2-х чисел равен разности их логарифмов: loga(x/y) = loga(x) – loga(y).

6. Дабы обнаружить логарифм числа, возведенного в степень, надобно логарифм самого числа умножить на показатель степени: loga(x^n) = n*loga(x). При этом показатель степени может быть любым числом — правильным, негативным, нулем, целым либо дробным.От того что x^0 = 1 для всякого x, то loga(1) = 0 для всякого a.

7. Логарифм заменяет умножение сложением, возведение в степень умножением, а извлечение корня делением. Следственно в неимение вычислительной техники логарифмические таблицы невидимо упрощают расчеты.Дабы обнаружить логарифм числа, не входящего в таблицу, его необходимо представить в виде произведения 2-х либо больше чисел, логарифмы которых есть в таблице, и обнаружить окончательный итог, сложив эти логарифмы.

Полезный совет
Число е – экспонента, ее значение равно 2,7182818281828…. Существует вестимая мнемоническая фраза для запоминания: «Экспоненту помнить метод есть легкой: два и семь десятых, двукратно Лев Толстой», где «Лев Толстой» = «1828» (год рождения писателя).

Совет 8: Как считать десятичные логарифмы

Десятичным логарифмом называют функцию для вычисления неведомого показателя степени, в тот, что возводится число десять. Почаще мы имеем дело с этой функцией, как с комбинированный частью физических либо математических формул, но изредка доводится изготавливать и фактические вычисления. Если у вас есть вероятность пользоваться компьютером, то, разумеется, никаких сложностей с нахождением значения десятичного логарифма появиться не должно.

Инструкция

1. Воспользуйтесь, скажем, вычислительными вероятностями поисковой системы Google – при наличии доступа в интернет это, вероятно, самый стремительный из допустимых методов вычисления десятичных логарифмов. Процедура применения поисковика максимально примитивна – перейдите на его основную страницу, наберите lg и через пробел введите число, десятичный логарифм которого вас волнует. Google произведет расчет и отобразит на странице итог. Если взамен обозначения lg вы наберете «десятичный логарифм», то и такое указание математического действия будет верно осознано поисковой системой.

2. Используйте устанавливаемое совместно с операционной системой приложение, имитирующее калькулятор, если доступа в интернет нет. В ОС Windows ее дозволено вызвать с подмогой диалога запуска программ – нажмите сочетание клавиш win + r, наберите calc (имя файла этой программы без растяжения) и щелкните по кнопке OK. В основном меню ОС тоже есть ссылка на запуск этого приложения – ищите ее в сегменты «Типовые» подраздела «Служебные» из раздела «Все программы». Ссылка эта так и названа – «Калькулятор».

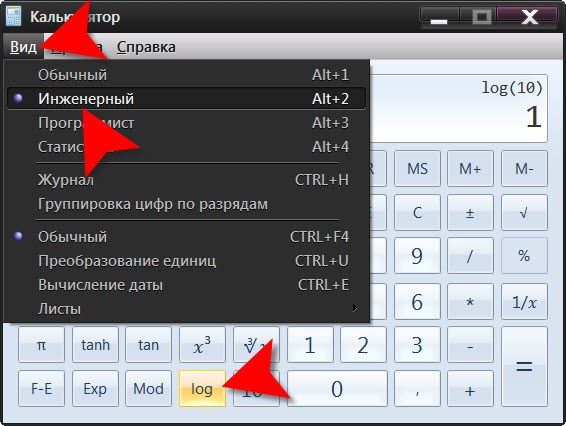
3. Нажмите сочетание клавиш alt + 2, дабы переключить приложение в «инженерный» режим. В больше ранних версиях Windows он назван «научным» – такую строку дозволено обнаружить в разделе «Вид» меню этой программы.

4. Введите число, десятичный логарифм которого вас волнует. Делать это дозволено как с клавиатуры, так и щелкая мышкой по соответствующим кнопкам в интерфейсе калькулятора на экране монитора. Обратите внимание, что тут для обозначения функции вычисления десятичного логарифма использована надпись log, а не привычное нам lg. Кликните по кнопке с символами log – калькулятор рассчитает и отобразит итог.

Видео по теме

Совет 9: Как обнаружить настоящий логарифм

Термин «логарифм » случился от 2-х греческих слов, одно из которых обозначает «число», а другое – «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую нужно построить непрерывное значение (основание), дабы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом “e”, то логарифм называют «естественным».

Вам понадобится

Инструкция

1. Воспользуйтесь во множестве представленными в интернете онлайн-калькуляторами – это, вероятно, самый стремительный и примитивный метод вычисления естественного логарифм а. Поиском соответствующего обслуживания вам заниматься не придется, потому что многие поисковые системы и сами имеют встроенные калькуляторы, абсолютно пригодные для работы с логарифм ами. Скажем, перейдите на основную страницу самого огромного сетевого поисковика – Google. Никаких кнопок для ввода значений и выбора функций тут не понадобится, примитивно наберите в поле ввода запроса необходимое математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию “e” введите ln 457 – этого будет абсолютно довольно, дабы Google отобразил положительный результат с точностью до восьми знаков позже запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.

2. Используйте соответствующую встроенную функцию, если надобность вычисления значения естественного логарифм а появляется при работе с данными в знаменитом табличном редакторе Microsoft Office Excel. Эта функция тут вызывается с применением общепризнанного обозначения такого логарифм а в верхнем регистре – LN. Выделите ячейку, в которой должен быть отображен итог вычисления, и введите знак равенства – так в этом табличном редакторе обязаны начинаться записи в ячейках, содержащих формулы. После этого наберите наименование функции (LN) и в скобках укажите числовое значение, логарифм которого требуется вычислить – скажем, =LN(457). Позже того, как вы нажмете Enter, в этой ячейке таблицы отобразится итог вычисления естественного логарифм а.

3. Откройте программу-калькулятор, которая устанавливается совместно с операционной системой, если оба приведенных выше метода вам не подходят. Обнаружить соответствующую ссылку в ОС Windows 7 дозволено, если раскрыть основное меню щелчком по кнопке «Пуск», а после этого ввести «каль» в поле «Обнаружить программы и файлы». Ссылка с наименованием «Калькулятор» будет первой строкой в итоге поиска. В иных версиях ОС ее нужно искать в подразделе «Типовые» раздела «Все программы» основного меню. Переключите калькулятор в больше функциональный режим, нажав сочетание клавиш Alt + 2. После этого введите значение, настоящий логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит итог.

Видео по теме

Совет 10: Как обнаружить десятичный логарифм

Десятичный логарифм – это частный случай операции вычисления показателя степени, в которую нужно построить основание (в данном случае – десятку), дабы получить начальное число. Из всеобщего ряда оснований чести быть выделенными в независимую операцию сегодня считаются каждого два числа. Помимо десятки это математическая константа, называемая «числом e», которая является основанием естественного логарифм а. Вычисление логарифм ов, включая десятичные, на современном ярусе становления компьютерной техники и средств коммуникаций трудности не представляет.

Вам понадобится

Инструкция

1. Рассчитайте десятичный логарифм во встроенном в операционную систему Windows калькуляторе. Дабы его запустить, кликните по кнопке «Пуск», наберите две буквы – «ка» – и нажмите клавишу Enter. Такой последовательностью действий вы принудите систему обнаружить приложения и файлы, начинающиеся с этих 2-х букв, и активировать первую строку списка итогов поиска – «Калькулятор».

2. Переключите приложение в «инженерный» вариант его интерфейса – нажмите комбинацию клавиш Alt + 2. Введите число, десятичный логарифм от которого требуется рассчитать, и кликните по четвертой слева кнопке в нижнем ряду интерфейса приложения – она помечена надписью log. На этом операция будет закончена, а итог отобразится в окошке калькулятора.

4. Дозволено обойтись вообще без вычислительных программ, а обратиться к поисковой системе Google. Данный поисковик имеет личный встроенный калькулятор, от вас понадобится лишь верно сформулировать запрос. Скажем, дабы вычислить десятичный логарифм числа 9,81 введите в поле поискового запроса log 9,81, нажмите кнопку отправки запроса и Google отобразит итог с точностью до девяти знаков позже запятой: log(9,81) = 0,991669007.

Видео по теме

Видео по теме

Обратите внимание!
Логарифм от числа, равного либо поменьше нуля, не существует и калькулятор в этом случае выдаст вам ошибку.

Полезный совет
Легко в уме дозволено посчитать логарифм единицы, он неизменно равен 0, а также логарифмы, которые являются степенью основания. Они легко будут равны этой степени.

Источник