Иллюстрированный самоучитель по MathCAD 11
Комплексные числа
Большинство операций в среде Mathcad по умолчанию осуществляются над комплексными числами. Комплексное число является суммой действительного и мнимого числа, получающегося путем умножения любого действительного числа на мнимую единицу (imaginary unit) i. По определению, i 2 =-1.
Чтобы ввести мнимое число, например 3i:
Для ввода мнимой единицы надо нажать клавиши 1, i. Если просто ввести символ «i», то Mathcad интерпретирует его как переменную i. Кроме того, мнимая единица имеет вид 1i, только когда соответствующая формула выделена. В противном случае мнимая единица отображается просто как i (рис. 4.1).

Рис. 4.1. Ввод мнимой единицы
Комплексное число можно ввести в виде обычной суммы действительной и мнимой частей или в виде любого выражения, содержащего мнимое число. Примеры ввода и вывода комплексных чисел иллюстрируются листингом 4.3.
Листинг 4.3. Комплексные числа:
Для работы с комплексными числами имеются несколько простых функций и операторов (см. разд. «Функции работы с комплексными числами» гл. 10), действие которых показано в листинге 4.4.
Листинг 4.4. Функций работы с комплексными числами:
Можно выводить мнимую единицу в результатах вычислений не как i, а как j. Для смены представления выберите нужное в списке Imaginary Value (Мнимое значение) диалогового окна Result Format (Формат результата), доступного по команде Format › Result › Display Options (Формат › Результат › Опции отображения).
Как в маткаде написать комплексное число
Глава 3. Работа с векторами и матрицами
MathCAD с одинаковым успехом вычисляет выражения с действительными и комплексными числами.
Комплексные числа можно записывать в любой принятой в математике форме:
– обычной (в виде суммы действительной и мнимой частей числа) – с=а+ b · i ;
– в тригонометрической форме – c = A ·( sin ( φ )+ i · cos (φ));
Для ввода мнимой единицы надо набрать с клавиатуры 1 i или 1 j и ввести число. При выведении курсора из области числа символ 1 исчезает, остается комплексное число в привычном виде (рис. 3.23 ).


расчет токов в цепи по уравнениям Кирхгофа ORIGIN:=1


Рис. 3. 23 Ввод комплексных чисел
Расчет напряжений по закону Ома 
без оператора векторизации выведено скалярное произведение векторов

это не аргумент функции—без вывод комплексно-сопряженных чисел
оператора векторизации не обойтись
Рис. 3. 24 Расчеты с векторами комплексных чисел
Модуль комплексного числа 
Аргумент комплексного числа вычисляется по формуле встроенной функцией arg ( A ), которая выдает угол поворота вектора в системе координат Re – Im (рис. 3.25 ).
модуль комплексного числа. необходим оператор векторизации

аргумент комплексного числа

угол в радианах угол в градусах
Рис. 3. 25 Вычисление модуля и аргумента комплексных чисел
MathCAD — это просто! Часть 19. Немного о работе с комплексными числами
Комплексные числа — одна из важнейших математических абстракций, очень часто используемая в реальных расчетах инженерами, физиками, электронщиками и другими специалистами. Само собой, настолько важная часть математики, как работа с комплексными числами, не могла остаться вне поля зрения разработчиков MathCAD’а. Сегодня мы с вами как раз и поговорим о том, как можно работать в MathCAD’е с ними — вы сможете самостоятельно убедиться в том, что это, в общем-то, не представляет каких-либо особых сложностей для пользователя этого мощнейшего математического пакета.
Комплексные числа в MathCAD: основы
Весь тот небольшой экскурс в работу с комплексными числами, который я привел выше, нужен только для того, чтобы напомнить (или, если кто-то не знал этого, то разъяснить), что же такое комплексные числа, и как именно с ними нужно работать. При работе в MathCAD’е, само собой, вам не понадобится собственноручно вычислять модуль и аргумент комплексного числа, не надо будет самостоятельно высчитывать степень экспоненты при перемножении комплексных чисел и даже не понадобится самому складывать действительную часть с действительной, а мнимую — с мнимой. Все за вас сделает этот мощный математический пакет. То есть, конечно, не все, а только черновую, вычислительную работу — постановка задачи и интерпретация результатов вычислений все равно останется за вами. Хорошая новость состоит в том, что для работы с комплексными числами не нужно как-то по- особенному настраивать среду MathCAD или применять какие-то новые арифметические операторы. Среда точно так же работает с комплексными числами, как и с действительными. Простой пример — сложение комплексных чисел. Попробуйте сложить два комплексных числа — например, 1+2i и 7-15i. Здесь, правда, стоит отдельно сказать пару слов относительно ввода в MathCAD’е мнимой единицы. Дело в том, что, если вы просто напишете ее как i, нажав на клавиатуре соответствующую клавишу, то система MathCAD посчитает, что вы ввели имя какой-либо переменной. Поэтому можно либо воспользоваться панелью инструментов Calculator (см. иллюстрацию, на которой нужная кнопка обведена кружком), либо вводить с клавиатуры комбинацию 1i.
После того, как вы попробуете складывать комплексные числа, можно попробовать их перемножать, чтобы убедиться в том, что MathCAD умеет делать и это. Можете попробовать возводить комплексные числа в какую-либо степень, а также любым другим образом поиздеваться над ними. Как и следовало ожидать, MathCAD с легкостью справляется с подобными заданиями. Поэтому вы можете работать с комплексными числами фактически точно так же, как и с действительными.
Комплексные числа в MathCAD: подробности и тонкости
Впрочем, конечно же, есть и некоторые тонкие моменты, связанные с отличиями в работе с комплексными и действительными числами. Самое главное из подобного рода отличий состоит, собственно говоря, в том, что операция извлечения корня с ними работает не совсем так, как надо — как, впрочем, и операция возведения в дробную степень, хотя для действительных чисел данные операции и абсолютно корректны. Дело в том, что на множестве комплексных чисел мы рассматриваем корень p n-й степени из числа z как множество решений уравнения pn = z. Если вы попробуете решить это уравнение с помощью оператора solve (хоть о нем мы говорили уже достаточно давно — думаю, вы еще не до конца забыли, как им пользоваться), то увидите, что для n-й степени это уравнение, согласно основной теореме алгебры, будет иметь ровно n решений. Если же для вычисления корня комплексного числа вы воспользуетесь операторами извлечения корня или возведения комплексного числа в дробную степень, то увидите, что подобные вычисления дадут вам только один корень из всех возможных, что не вполне корректно. Впрочем, в ряде практических задач вам будет нужен только один корень, но все равно его лучше получать с помощью solve, а затем уже выбирать среди результатов.
Ну, и напоследок такой вопрос: а как лучше обозначать мнимую единицу? Дело в том, что в литературе встречается два варианта ее обозначения: i и j. Первый более характерен для советских и постсоветских источников, второй — для зарубежных. Вполне может случиться так, что вам потребуется в вашем проекте использовать второе, а не первое, которое используется в MathCAD по умолчанию. Конечно же, эта мощная математическая среда позволяет нам изменить обозначение мнимой единицы на то, которое будет для нас наиболее удобным. Для того, чтобы поменять обозначение, нужно в меню Format выбрать пункт Result, а в появившемся окне на вкладке Display Options заменить параметр Imaginary Value. Вариантов этого параметра, конечно, не много — собственно, их всего два: либо i, либо j. Но больше вариантов, собственно говоря, и нету.
Итак, мы с вами познакомились с комплексными числами, а также с тем, как именно работать с ними в MathCAD’е. Вы смогли сами убедиться, что это совсем несложно, хотя, конечно, некоторые вычисления и имеют свои тонкости. Но тонкости есть везде, и главное — быть заранее готовым к тому, что есть немалый шанс с ними столкнуться. Поэтому, если вы внимательно читаете статьи серии «MathCAD — это просто», то будете хорошо подготовлены к встречам с различными неожиданностями в среде MathCAD. Успехов вам в работе с этим мощным математическим пакетом и интересных вычислений!
Компьютерная газета. Статья была опубликована в номере 33 за 2008 год в рубрике soft
Как в маткаде написать комплексное число
Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.
Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить 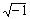
Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.
При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.
Специальные операции над комплексными числами
В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:
Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.
Рисунок 2: Комплексные числа в Mathcad.
При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.
Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.
Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.
Рисунок 3: Нахождение вещественных корней n—ой степени из отрицательного числа.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Как в маткаде написать комплексное число
Примечание
Если вы продолжите листинг 4.1 последовательным выводом всех переменных, то с удивлением обнаружите, что некоторые из чисел выглядят по-иному (например, число d=0). Объяснение этому будет дано в разд. 4.2.
Примечание
В логических функциях используются битовые числа (ложь или истина). Они в MathCAD обозначаются обычными действительными числами о и 1.
Рис. 4.1. Ввод мнимой единицы
Комплексное число можно ввести в виде обычной суммы действительной и мнимой частей, или в виде любого выражения, содержащего мнимое число. Примеры ввода и вывода комплексных чисел иллюстрируются листингом 4.3.
Листинг 4.3. Комплексные числа
Для работы с комплексными числами имеются несколько простых функций и операторов (см. разд. «Функции работы с комплексными числами» гл. 10), действие которых показано в листинге 4.4.
Листинг 4.4. Функции работы с комплексными числами
Примечание
Можно выводить мнимую единицу в результатах вычислений не как i, а как j. Для смены представления выберите нужное в списке Imaginary Value (Мнимое значение) диалогового окна Result Format (Формат результата), доступного по команде Format / Result / Display Options (Формат / Результат / Опции отображения).
Примечание
Совершенно аналогичным образом можно определять пользовательские функции строкового типа.
Рис. 4.3. Вставка единиц измерения размерной величины
Рис. 4.4. Диалоговое окно Insert Unit
Рис. 4.6. Нельзя складывать переменные разной размерности
Рис. 4.7. Изменение единиц измерения в ответе
Над размерными переменными можно производить любые корректные с физической точки зрения расчеты. Пример расчета сопротивления через отношение напряжения к току приведен в листинге 4.8.
Листинг 4.8. Расчеты с размерными переменными
Обратите внимание, что результат в листинге 4.8 выдан не в омах. Тем не менее, легко перевести его в омы, как и в другие единицы. Для этого достаточно дважды щелкнуть на местозаполнителе, присутствующем после вычисленного значения формулы в момент, когда она выделена (рис. 4.7, внизу). В результате появляется то же самое диалоговое окно Insert Unit (Вставка единицы измерений), в котором можно поменять единицу измерений вычисленного ответа. В результате ответ будет пересчитан в соответствии с вновь введенной единицей измерения (как сделано для верхней формулы на рис. 4.7).
Примечание
Можно включить автоматический перевод единиц измерения в более простые единицы. Для этого перейдите в диалоговое окно Result Format (Формат результата) на вкладку, посвященную размерностям, с помощью команды For
mat/ Result/ Unit Display (Формат/ Результат/ Отображение размерности).
Установите в ней флажок Simplify units when possible (Упрощать единицы, когда это возможно).
Процесс смены единиц в момент их выбора в диалоге Insert Unit (Вставка единицы измерений) показан на рис. 4.8. В результате приведенного выбора выведенное в амперах значение силы тока будет изменено на значение в килоамперах: i.oi кд.
Рис. 4.9. Создание ранжированной переменной
Чтобы создать ранжированную переменную с шагом, не равным 1, например, 0,2, 4, 6, 8:
1. Создайте ранжированную переменную в диапазоне от о до 8 (см. рис. 4.9).
2. Поместите линии ввода на значение начала диапазона (о).
3. Введите запятую.
4. В появившийся местозаполнитель (рис. 4.11) введите значение шага изменения ранжированной переменной (2).
Созданная ранжированная переменная будет иметь значения от о до 8 включительно, с шагом, равным 2.
Рис. 4.10. Вывод ранжированной переменной
Рис. 4.11. Создание ранжированной переменной с шагом, не равным 1
Чаще всего ранжированные переменные используются:
— при параллельных вычислениях (листинги 4.13 и 4.14);
— для присвоения значений элементам других массивов (листинги 4.14
и 4.15).
Обратите внимание на типичный пример использования ранжированной пременной из листингов 4.13 и 4.14. Большинство математических действий, реализованных в MathCAD, совершаются над ранжированными переменными точно так же, как над обычными числами. В этом случае одно и то же действие осуществляется параллельно над всеми элементами ранжированной переменной.
Листинг 4.13. Ранжированная переменная
при параллельных вычислениях
Примечание
Параллельные вычисления производятся точно так же и над произвольными векторами, не обязательно являющимися ранжированными переменными. Например, можно определить в листинге 4.14 вектор 1, подобно вектору из листинга 4.10, и провести те же параллельные вычисления над его элементами.
Рис. 4.12. Вставка матрицы
Рис. 4.13. Заполнение матрицы элементами
На рис. 4.14 и 4.15 показаны результаты последовательной вставки в матрицу столбца и строки после определения соответствующего числа столбцов и строк в диалоге Insert Matrix и нажатия в нем кнопки Insert (Вставить).
Рис. 4.14. Добавление одного столбца к матрице
Рис. 4.15. Добавление одной строки к матрице
В местозаполнители элементов матрицы можно вставлять не только числа (действительные или комплексные), но и любые математические выражения, состоящие из переменных, операторов, встроенных и пользовательских функций (листинг 4.16, вторая строка).
Листинг 4.16. Использование переменных и функций
при определении матрицы
Создание массива определением его отдельных элементов
Самый простой способ создания массива заключается в определении любого количества его элементов. Это можно сделать:
— присваивая значения непосредственно отдельным элементам массива;
— применяя ранжированные переменные (см. листинг 4.15).
Любой из этих способов позволяет присвоить нужное значение как всем элементам массива (см. листинг 4.15), так и части из них, либо даже одному-единственному элементу. В последнем случае создается массив, размерность которого задается индексами введенного элемента (листинг 4.17), а неопределенным элементам по умолчанию присваиваются нулевые значения.
Лиcтинг: 4.17. Создание матрицы определение одного ее элемента
В любом месте документа допускается как переопределение любого из элементов массива (листинг 4.18, первая строка), так и изменение его размерности. Чтобы поменять размерность всего массива, просто присвойте любое значение новому элементу, индексы которого выходят за границы прежней размерности (вторая строка листинга 4.18).
Примечание
В местозаполнители элементов матрицы допускается вставка любых функций, подобно применению обычного оператора присваивания.
Cовет
Процесс создания тензора автоматизирует применение ранжированных переменных.
Обратите внимание, что MathCAD по умолчанию не отображает трехмерную структуру тензора (предпоследняя строка листинга 4.19), а вместо этого показывает информацию о размерах каждого элемента матрицы s. Развернуть вложенные массивы можно с помощью команды Format / Result / Display Options (Формат / Результат / Опции отображения), устанавливая флажок Expand Nested Arrays (Разворачивать вложенные массивы) на вкладке Display Options (Опции отображения).
Создание таблицы ввода
В документе MathCAD могут присутствовать разнообразные объекты, созданные в других приложениях. Например, если в буфер обмена скопирован фрагмент таблицы с данными из другого приложения (например, Microsoft Excel), то можно использовать его при создании матрицы с помощью таблицы ввода. Для этого:
1. Поместите щелчком мыши курсор ввода на пустое место документа.
2. Выберите в главном меню на пустом месте Insert / Component / Table (Вставка / Компонент / Таблица).
3. В окне Component Wizard (Мастер компонентов) выберите элемент списка Input Table (Таблица ввода) и нажмите в нем кнопку Finish (Завершить) (рис. 4.16).
4. Вставьте имя матрицы в местозаполнитель и данные в ячейки появившейся в документе таблицы ввода (рис. 4.17). Учтите, что в таблицу можно вставлять фрагменты из буфера обмена, любые действительные или комплексные числа, но нельзя использовать формулы.
Рис. 4.16. Окно Мастера компонентов
Матрица, определенная с помощью таблицы ввода, выглядит точно так же, как при обычном определении (листинг 4.20).
Рис. 4.17. Ввод чисел в таблицу данных
Листинг 4.20. Матрица, определенная в таблице данных (рис. 4.17)
Создание массивов путем импорта из других приложений
С помощью Мастера компонентов (Component Wizard), вызываемого командой Insert / Component / Table (Вставка / Компонент / Таблица) легко устанавливать связь с другими компонентами, импортируя оттуда данные. Подробнее об этом можно прочитать в справочной системе MathCAD в статьях:
— Excel Component (Вставка компонента Excel);
— MATLAB Component (Вставка компонента MATLAB).
4.3.4. Отображение вывода векторов и матриц
Вы, вероятно, обратили внимание, что матрицы, векторы и ранжированные переменные отображались в различных примерах по-разному. Это связано с автоматическими установками отображения матриц, принятыми в MathCAD по умолчанию. Существуют два стиля отображения массива: в форме матрицы и в форме таблицы (рис. 4.18).
Рис. 4.19. Изменение стиля отображения массива
Стиль отображения в виде таблицы допускает различное выравнивание матрицы относительно выражения слева от оператора вывода (рис. 4.20). Для изменения выравнивания вызовите контекстное меню из области таблицы, наведите в нем указатель мыши на пункт Alignment (Выравнивание) и в подменю выберите тип выравнивания.
Рис. 4.20. Различные стили выравнивания матриц
В диалоговом окне Result Format (Формат результата), помимо стиля отображения матрицы, можно задать стиль отображения тензоров (вложенных массивов). Для того чтобы отображать тензоры в стиле, показанном на рис. 4.21, установите флажок Expand nested arrays (Разворачивать вложенные массивы). Чтобы отображать их в свернутой форме (см. листинг 4.19), снимите этот флажок.
Примечание
Количество десятичных знаков левого сомножителя числа с порядком контролируется в некоторых форматах первым из трех перечисленных параметров.
— кроме того, число с порядком может представляться в эквивалентных видах: «1,23х10 2 » или с порядком в инженерном формате (engineering format): «1.23Е+002».
— MathCAD имеется несколько типов форматов, в каждом из которых разрешается изменение различных параметров представления числа. Формат выбирается на вкладке Number Format (Формат числа) диалогового окна Result Format (Формат результата) (рис. 4.22).
Рис. 4.24. Задание порога мнимого нуля
Рис. 4.26. Задание вывода результата в других системах счисления
Листинг 4.25. Форматирование вывода чисел в других системах счисления
Примечание
Мы рассмотрели в этой главе основные принципы наиболее простого численного ввода и вывода данных. О более впечатляющих формах ввода-вывода (графики, анимация, ввод-вывод в файлы) рассказывается в последней части книги (см. гл. 15).


























