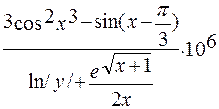Основные математические функции MatLab
В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.
Некоторые часто используемые математические функции:
· exp(x)–экспонента числа x;
· log(x)– натуральный логарифм;
· log10(x)– десятичный логарифм;
· sqrt(x)– квадратный корень;
· abs(x)– абсолютное значение x;
· mod(x, y)– остаток от целочисленного деления с учетом знака;
· rem(x, y)– остаток от целочисленного деления без учета знака;
· real(z)– вещественная часть комплексного числа;
· imag(z)– мнимая часть комплексного числа;
· round(x)– округление до ближайшего целого.
Более полный список основных математических функций MatLab:
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x,y) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:
Вычислить: res= 
Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.
Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные. Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.
res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – m.
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить нужный каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Дата добавления: 2016-04-02 ; просмотров: 5455 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Основные математические функции MatLab
MatLab содержит в себе все распространенные математические функции, которые доступны по их имени при реализации алгоритмов. Например, функция sqrt() позволяет вычислять квадрат числа и может быть использована в программе следующим образом:
Аналогичным образом вызываются и все другие математические функции, представленные в табл. 1.2.
Таблица 1.2. Основные математические функции MatLab
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
Почти все элементарные функции допускают вычисления и с комплексными аргументами. Например:
Ниже показан пример задания вектора с именем a, и содержащий значения 1, 2, 3, 4:
a = [1 2 3 4]; % вектор-строка
Для доступа к тому или иному элементу вектора используется следующая конструкция языка:
disp( a(1) ); % отображение значения 1-го элемента вектора
disp( a(2) ); % отображение значения 2-го элемента вектора
disp( a(3) ); % отображение значения 3-го элемента вектора
disp( a(4) ); % отображение значения 4-го элемента вектора
т.е. нужно указать имя вектора и в круглых скобках написать номер индекса элемента, с которым предполагается работать. Например, для изменения значения 2-го элемента массива на 10 достаточно записать
a(2) = 10; % изменение значения 2-го элемента на 10
Часто возникает необходимость определения общего числа элементов в векторе, т.е. определения его размера. Это можно сделать, воспользовавшись функцией length() следующим образом:
N = length(a); % (N=4) число элементов массива а
Если требуется задать вектор-столбец, то это можно сделать так
a = [1; 2; 3; 4]; % вектор-столбец
b = [1 2 3 4]’; % вектор-столбец
при этом доступ к элементам векторов осуществляется также как и для векторов-строк.
Следует отметить, что векторы можно составлять не только из отдельных чисел или переменных, но и из векторов. Например, следующий фрагмент программы показывает, как можно создавать один вектор на основе другого:
a = [1 2 3 4]; % начальный вектор a = [1 2 3 4]
b = [a 5 6]; % второй вектор b = [1 2 3 4 5 6]
Здесь вектор b состоит из шести элементов и создан на основе вектора а. Используя этот прием, можно осуществлять увеличение размера векторов в процессе работы программы:
a = [a 5]; % увеличение вектора а на один элемент
Недостатком описанного способа задания (инициализации) векторов является сложность определения векторов больших размеров, состоящих, например, из 100 или 1000 элементов. Чтобы решить данную задачу, в MatLab существуют функции инициализации векторов нулями, единицами или случайными значениями:
a1 = zeros(1, 100); % вектор-строка, 100 элементов с
% нулевыми значениями
a2 = zeros(100, 1); % вектор-столбец, 100 элементов с
% нулевыми значениями
a3 = ones(1, 1000); % вектор-строка, 1000 элементов с
% единичными значениями
a4 = ones(1000, 1); % вектор-столбец, 1000 элементов с
% единичными значениями
a5 = rand(1000, 1); % вектор-столбец, 1000 элементов со
% случайными значениями
Матрицы в MatLab задаются аналогично векторам с той лишь разницей, что указываются обе размерности. Приведем пример инициализации единичной матрицы размером 3х3:
E = [1 0 0; 0 1 0; 0 01]; % единичная матрица 3х3
E = [1 0 0
0 1 0
0 0 1]; % единичная матрица 3х3
Аналогичным образом можно задавать любые другие матрицы, а также использовать приведенные выше функции zeros(), ones() и rand(), например:
A1 = zeros(10,10); % нулевая матрица 10х10 элементов
A2 = zeros(10); % нулевая матрица 10х10 элементов
A3 = ones(5); % матрица 5х5, состоящая из единиц
A4 = rand(100); % матрица 100х100, из случайных чисел
Для доступа к элементам матрицы применяется такой же синтаксис как и для векторов, но с указанием строки и столбца где находится требуемый элемент:
A = [1 2 3;4 5 6;7 8 9]; % матрица 3х3
disp( A(2,1) ); % вывод на экран элемента, стоящего во
% второй строке первого столбца, т.е. 4
disp( A(1,2) ); % вывод на экран элемента, стоящего в
% первой строке второго столбца, т.е. 2
Также возможны операции выделения указанной части матрицы, например:
B1 = A(:,1); % B1 = [1; 4; 7] – выделение первого столбца
B2 = A(2,:); % B2 = [1 2 3] – выделение первой строки
B3 = A(1:2,2:3); % B3 = [2 3; 5 6] – выделение первых двух
% строк и 2-го и 3-го столбцов матрицы А.
Размерность любой матрицы или вектора в MatLab можно определить с помощью функции size(), которая возвращает число строк и столбцов переменной, указанной в качестве аргумента:
a = 5; % переменная а
A = [1 2 3]; % вектор-строка
B = [1 2 3; 4 5 6]; % матрица 2х3
size(a) % 1х1
size(A) % 1х3
size(B) % 2х3
Как в матлабе пишется степень
ЛАБОРАТОРНАЯ РАБОТА №1
2. Операции умножения, деления (*, /).
4. Извлечение из квадратного корня ( sqrt ): sqrt (16+9)
5. Повторение действий, повторение с измененными параметрами и функциями.
6. Невыполняемый комментарий — %
7. Задание ряда чисел с заданным шагом и по умолчанию: t=(0:0.5:7)’ % В виде столбца
8. Задание матриц (например: a = [1 2 3;4 5 6]):
9. Матричные операции:
— возведение в степень ( ^ ) ;
— c оздание нижней треугольной матрицы А: tril (А).
— c оздание верхней треугольной матрицы А: triu (А).
¾ вращение матрицы А относительно вертикальной оси: fliplr ( A ).
¾ вращение матрицы А относительно горизонтальной оси: flipud ( A ).
¾ поворот матрицы А на 90 0 против часовой стрелки: rot 90( A ).
¾ п.п. вращения и поворота выполнить для квадратных и прямоугольных матриц.
¾ формирование единичной матрицы заданного размера n : eye ( n ).
¾ формирование единичной матрицы по размеру данной квадратной матрицы А: eye ( size ( A )).
¾ матрица единиц по размеру заданной матрицы А: ones ( size ( A )).
¾ матрица нулей по размеру заданной матрицы А: zeros ( size ( A )).
¾ матрица Паскаля данного размера n : pascal ( n ). Матрица Паскаля является положительно-определенной.
¾ извлечение диагонали заданной матрицы А: diag ( A ).
¾ вычисление следа матрицы А: trace ( A ).
¾ вычисление следа матрицы А через функции sum и diag : sum ( diag ( A )).
¾ магический квадрат размера n ( n >2): magic ( n ).
¾ проанализировать магический квадрат с помощью функций MATLAB : просуммировать элементы каких-либо строк или столбцов, найти след магического квадрата.
¾ создание диагональной матрицы по заданной матрице А: diag ( diag ( A )).
¾ создание диагональной матрицы по заданному вектору-столбцу Р: diag ( P ).
¾ создание диагональной матрицы по заданному вектору-строке N : diag ( N ).
¾ собственные числа действительной или комплексной матрицы А: eig ( A ).
¾ выделение строк или столбцов матрицы: A = [1 2 3;4 5 6]; A (:,2:3) — 2-й и 3-й столбцы
¾ Задание матриц по случайному равномерному закону — rand (например, rand (3,4))
¾ Задание матриц по случайному нормальному закону — randn (например, randn (2,5))
¾ Операции с массивами (перед знаком арифметического действия ставится точка):
(например: [1 2 3;4 5 6].^2) — возведение каждого элемента матрицы в квадрат.
Выполнить матричные операции п.9 в виде операций с массивами.
8. Формирование коэффициентов характеристического полинома заданной числовой матрицы А: poly ( A ).
9. Формирование характеристического полинома заданной числовой матрицы А: poly ( sym ( A )). По умолчанию независимой переменной полинома является х.
10. Формирование характеристического полинома заданной числовой матрицы А с назначаемой независимой переменной полинома (например s ): poly ( sym ( A ), sym (‘ s ‘)).
11. Сравнить результаты выполнения п.п. 1.26, 1.27, 1.28.
12. Формирование коэффициентов характеристического полинома матрицы А по ее заданным собственным числам: poly ( eig ( A )).
13. Формирование характеристического полинома по заданным корням, являющимися элементами вектора Р : poly ( P ).
14. Формирование полинома с коэффициентами, являющимися элементами заданного вектора Р: poly 2 sym ( P ). Степень полинома на единицу меньше размерности заданного вектора Р.
1. Размерность матрицы А: size ( A ).
2. Длина вектора Р: length ( P ).
3. Применить функцию size к вектору Р, примениить функцию length к матрице А (к прямоугольной и квадратной).
4. Уплотненный вывод на экран массивов и чисел: disp ( A ), disp ( P ), disp ( a ), где а — какое-либо число (действительное или комплексное, например, а=2+3 i ).
7. Определение знак заданного числа а: sign ( a ). Аргументом функции sign могут быть числа, выражения, математические функции.
8. Округление числа а до ближайшего целого: round ( a ).
9. Абсолютное значение заданного числа или выражения — abs : abs ((3-5)/2), abs (-2^3)
III. Специальные функции.
1. Разложение числа N на простые множители: factor ( N ).
2. Суммирование элементов вектора Р: sum ( P ). Результат — число.
3. Суммирование элементов столбцов матрицы А: sum ( A ). Результат — строка, состоящая из суммы элементов каждого столбца матрицы А.
4. Формирование произведения элементов вектора Р: prod ( P ).
5. Формирование произведения элементов столбцов матрицы А: prod ( A ).
6. Формирование матрицы с элементами из возможных перестановок элементов заданного числового вектора Р: perms ( P ).
Создание М-файлов в виде М-сценариев.
1. Создание простейших сценариев.
10. Создать в командном окне MATLAB матрицу: а = [1 2 3;4 5 6] или а = [1,2,3;4,5,6];
11. Транспонировать матрицу а : а1 = а ‘ ;
12. Создать матрицу b = [10 20 30;40 50 60];
13. Перемножить матрицы а1 и b : с = а1* b ;
14. На экране создать надпись ‘Перемножение матриц а1 и b :’ с помощью disp (‘Перемножение матриц а1 и b : ‘);
15. Вывести результат перемножения, набрав в командной строке обозначение с и нажав клавишу Enter ;
17. Проделать предыдущие пункты команд с точкой с запятой и без.
Формирование выборки случайных чисел, распределенных по экспоненциальному закону.
Функция распределения экспоненциального распределения вероятностей:
(1)
где 
— интенсивность распределения, равная обратной величине математического ожидания (среднего) распределения, т.е. 
где 
— математическое ожидание.
Выборка случайных чисел определяется через инверсную функцию от F ( t ):
(2)
где 
— случайное число из интервала [0, 1], 
1. Сценарий формирования выборки случайных чисел, распределенных по экспоненциальному закону.
1.1. Выборка из 18 случайных чисел с экспоненциальным распределением и с заданным параметром интенсивности, равным 2:
% начало цикла, шаг индексации равен 1
% 
— случайное число из [0, 1]
% окончание цикла
% получение вектора-столбца случайных чисел
% сортировка случайных чисел по возрастанию значений
1.2. Формирование выборки 18 случайных чисел с экспоненциальным распределением с помощью встроенной функции expinv :
1.3. Формирование выборки 18 случайных чисел с экспоненциальным распределением с помощью встроенной функции exprnd :
R = sort ( y ) % R — вектор случайных отсортировнных чисел по возрастанию
Примеры статистичесих интерактивных графических окон
функций распределения вероятностей.
Диалоговое (интерактивное) окно графических типовых распределений вероятностей в системе MATLAB — функция DISTTOOL ( disttool ).
DISTTOOL позволяет наглядно в виде графиков представлять различные функции распределения вероятностей с задаваемыми параметрами. В DISTTOOL приводятся две функции: cdf — функция распределения (интегральная функция распредления вероятностей), pdf — функция плотности распределения (дифференциальная функция распределения вероятностей).
Диалоговое (интерактивное) окно графических типовых гистограмм распределения вероятностей в системе MATLAB — функция RANDTOOL ( randtool ).
RANDTOOL позволяет представлять гистограммы функций плотности распределения вероятностей с возможным изменением параметров распределения и с изменением количества интервалов рассматриваемой гистограммы.
2.1. График в полярной системе координат:
2.2. Совмещение графиков в одной системе координат с помощью функции hold on : t =0:0.01:2* pi ; y 1=3*(1+ sin ( t )); y 2=3*(1- sin ( t ));
2.3. Совмещение трех и более графиков с помощью функции hold on :
2.4. График в декартовой системе координат:
2.5. Формирование пояснений к графику с помощью функции gtext :
% требуемые символы ( t и y ) устанавливаются в позиции курсора мыши.
% График функции sin ( t ) или sin ( x ) и т.д. в пределах по аргументу от 
до 
:
» fplot(‘sin(t)’,[-3*pi 3*pi]),grid % Набор в рабочей строке MATLAB
% Совмещение нескольких графиков: sin ( t ), exp (-0.5 t ), 3 cos ( t )
Задание: Построить с помощью fplot графики следующих функций и их комбинаций:
с соответствующими областями определения.
t =0:0.01:2* pi ; y = sin ( t );
ylabel(‘ функция ‘),gtext(‘t’),gtext(‘y’)
% требуемые символы 
на графике устанавливаются в позиции курсора мыши.
2.8. Формирование пояснений к начертанию нескольких графиков с помощью функции legend :
plot(t,y1,’r’),grid,hold on,plot(t,y2), legend(‘s1′,’c2’)
2.9. Установка ярлыка legend в различных частях графика:
в левом верхнем углу: legend (‘ s 1′,’ c 2′, 2);
в левом нижнем углу: legend (‘ s 1′,’ c 2′, 3);
в правом нижнем углу: legend (‘ s 1′,’ c 2′, 4);
в правом верхнем углу: legend (‘ s 1′,’ c 2′, 1)
или по умолчанию: legend (‘ s 1′,’ c 2′);
В командной строке MATLAB набрать функцию funtool и запустить на выполнение ( Enter ). Самостоятельно проделать возможные построения и вычисления: графики стандартных функций, дифференцирование и интегрирование функциональных выражений, обращение функций, сложение двух функций и т.д.
% Установка для графиков цветов осуществляется в соответствии со следующими ключевыми обозначениями, приведенными в табл.1.: