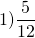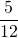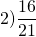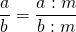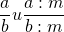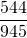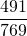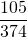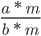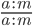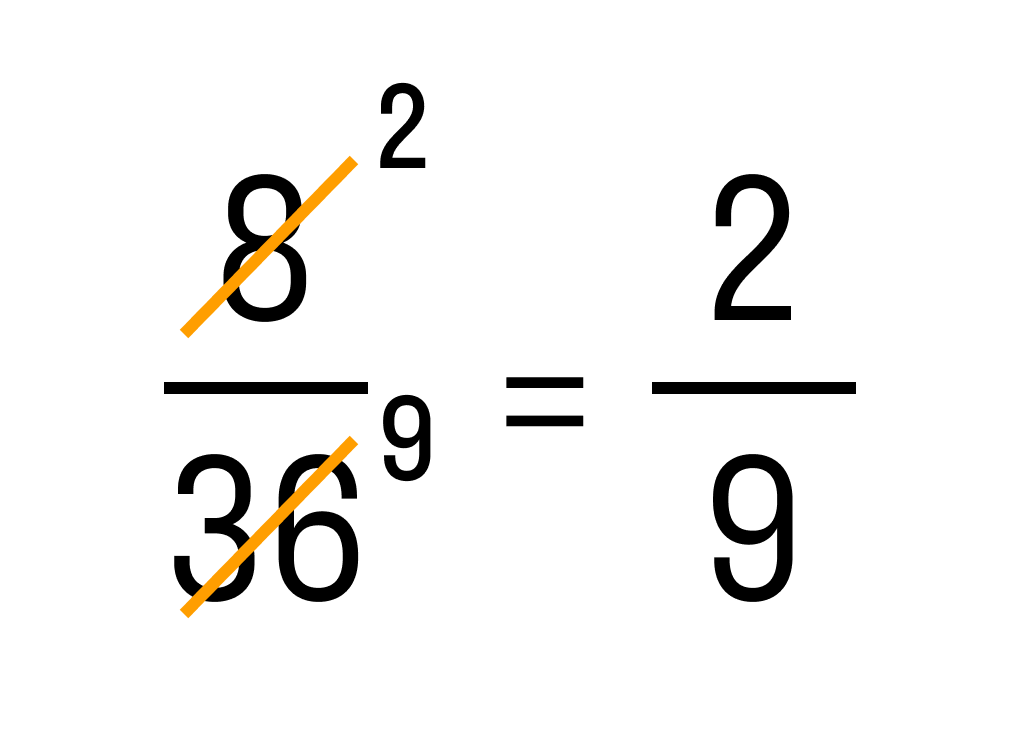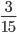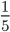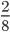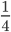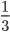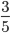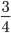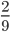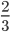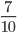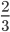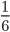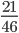Как сокращать дроби: простые примеры с подробными решениями
Содержание:
В этой статье коротко предоставим информацию о том, как сокращать дроби. Сначала приведем немного теоретической части, а затем подкрепим ее решением практических задач.
Что означает сократить дробь
Как сокращаются дроби
Как привести дробь к несократимому виду
Обычно алгебраическое решение любой задачи по сокращению дробей сводится к получению равной дроби, но в несокращаемом виде. Чтобы получить несократимую дробь, ее делят на определенное число, которое называется наибольший общий делитель (сокращенно НОД):
Практически рассмотрим, используя дробь \frac < 6 > < 12 >. Ее можно сократить на НОД, который равняется 6. Тогда 6 : 6 = 1 и 12 : 6 = 2. Следовательно:
Последняя дробь является несократимой.
Следует обратить внимание, что в большинстве случаев если требуется выполнить сокращение дробей, то это значит выполнить до получения несократимой дроби.
Как сократить большую дробь
В качестве нового примера возьмем дробь 144192. Сначала найдем наибольший общий делитель для чисел 144 и 192. Для этого можно применить метод разложения на простые множители:
144 : 2 = 72 192 : 2 = 96
72 : 2 = 36 96 : 2 = 48
36 : 2 = 18 48 : 2 = 24
18 : 2 = 9 24 : 2 = 12
Тогда наибольшим общим множителем для данных чисел будет число 48 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 2.
Разделив исходную дробь на 48 получим несократимую дробь:
Разберем еще один способ, который позволяет сокращать числитель и знаменатель дроби последовательно на делитель, который без труда определяется по простейшим математическим признакам. Если требуется сократить дробь типа 40008 800, то можно сразу же определить, что здесь присутствует общий множитель 100, который можно вынести за скобку:
Далее невооруженным глазом заметно, что оба числа делятся на 2, а результат опять на 2 и т. д. В конечном итоге получаем несократимую дробь \frac < 5 > < 11 >= \frac < 4000 > < 8800 >. Теперь можно сказать, что наибольшим общим делителем для данной дроби было число 800.
В заключении заметим, что если знаменатель дроби представляет собой числитель, возведенный в квадрат, то такая дробь в несокращаемом виде всегда будет представлять собой: 1 – в числителе + число, значившееся числителем до сокращения, в знаменателе:
Сократимые дроби
Вы будете перенаправлены на Автор24
Сократимые и несократимые дроби
Все обыкновенные дроби делятся на сократимые и несократимые дроби. Такое разделение дробей зависит от наличия или отсутствия общих делителей числителя и знаменателя, отличных от единицы.
Правила проверки дроби на сократимость
В самых простых случаях проверить дробь на сократимость можно с помощью признаков делимости.
Готовые работы на аналогичную тему
Правило проверки обыкновенной дроби на сократимость
Вычислить наибольший общий делитель (НОД) числителя и знаменателя данной дроби:
Решение.
НОД вычислим по алгоритму Евклида:
Сокращение дробей
Чтобы сократить дробь, нужно ее числитель и знаменатель разделить на их общий положительный отличный от единицы делитель. В результате сокращения дроби получают новую дробь, равную исходной, но с меньшим числителем и знаменателем.
Приведение обыкновенных дробей к несократимому виду
Таким образом, для приведения обыкновенной дроби к несократимому виду необходимо ее числитель и знаменатель разделить на их НОД.
Под фразой «сократите дробь» чаще всего подразумевают приведение исходной дроби к несократимому виду. Т.е. именно деление числителя и знаменателя на их НОД, а не деление на любой их общий делитель.
Правило сокращения дробей
Найти НОД числителя и знаменателя дроби.
Разделить числитель и знаменатель дроби на их НОД, в результате чего получают несократимую дробь, равную исходной.
Решение.
Воспользуемся правилом сокращения дробей:
Наиболее удобным является алгоритм Евклида:
\[231=187\cdot 1+44\]\[187=44\cdot 4+11\]\[44=11\cdot 4\]
Таким образом, НОД($187, 231)=11$.
Иногда для сокращения дробей (в более простых случаях) применяют способ \textit<разложения дроби на простые множители>, после чего убираются все общие множители из числителя и знаменателя. Этот способ вытекает из правила сокращения дробей, т.к. НОД равен произведению всех общих простых множителей числителя и знаменателя.
Решение.
Разложим числитель и знаменатель на простые множители:
Избавимся от общих множителей в числителе и знаменателе (для удобства их часто зачеркивают):
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 21 06 2021
Несократимая дробь
Несократимая дробь — это дробь, числитель и знаменатель которой являются взаимно-простыми числами.
То есть единственным общим делителем числителя и знаменателя несократимой дроби является единица.
Делители числителя: 1; 5
Делители знаменателя: 1 ; 2; 3; 4; 6; 12.
НОД (5; 12) =1, следовательно, 5 и 12 — взаимно-простые числа. Поэтому дробь
Делители числителя: 1 ; 2; 4; 8; 16.
Делители знаменателя: 1 ; 3; 7; 21.
Наибольший (и единственный) общий делитель числителя и знаменателя — единица. Значит, числитель и знаменатель — взаимно-простые числа. Поэтому данная дробь — несократимая.
Согласно основному свойству дроби, дробь не изменится, если её числитель и знаменатель разделить на одно и то же число, отличное от нуля:
— две различные записи одного и того же числа.
В математике принято ответ записывать в виде несократимой дроби. То есть если числитель и знаменатель дроби можно разделить на одно и то же число, необходимо это сделать, иначе ответ не считается правильным.
Вот почему столь важно уметь определять, является ли дробь несократимой.
Как определить, является ли дробь несократимой?
1) Можно разложить числитель и знаменатель на простые множители и найти наибольший общий делитель. Если он равен 1, дробь несократима.
— несократимая дробь, поскольку наибольший общий делитель числителя и знаменателя равен единице и 544 и 945 — взаимно-простые числа.
2) Если числитель и знаменатель — простые числа, то они являются взаимно-простыми, а дробь, соответственно, — несократимой.
несократима, так как 491 и 769 — простые числа (проверили по таблице простых чисел).
3) Можно проверять делимость числителя и знаменателя, используя признаки делимости.
Если ни один из делителей одного числа не является делителем другого, то общий делитель числителя и знаменателя — единица, то есть они являются взаимно-простыми числами, а дробь — несократимой.
Числитель 105 делится на 5, 105:5=21. 21 делится на 3 и на 7. Следовательно, делители 105: 1; 3; 5; 7; 105.
Искать все делители знаменателя 374 не обязательно. Достаточно проверить, а не делится ли он на один из делителей числителя:
на 5 не делится (запись заканчивается не на 0 и не на 5),
на 7 не делится (можно проверить непосредственным делением),
Значит 1 — единственный общий делитель 105 и 374, они являются взаимно-простыми числами, а дробь — несократимой.
Сокращение обыкновенных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:


где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Больше наглядных примеров и понятных объяснений — на курсах обучения математике в онлайн-школе Skysmart.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.

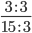
Сокращение выполнено: 
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.

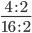
Сокращение выполнено: 
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
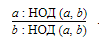
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1

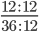
Сокращение выполнено: 
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3

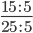
Сокращение выполнено: 
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.

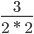
Сокращение выполнено: 
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9

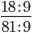
Сокращение выполнено: 
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:

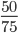
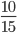
Сокращение выполнено: 
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

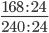
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

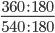
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

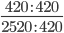
Сокращение выполнено. Дробь приведена к несократимому виду: 
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

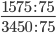
Сокращение выполнено. Дробь приведена к несократимому виду: 
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.