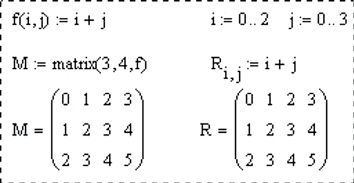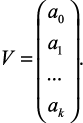Слово Как написать котангенс в маткаде - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Как написать котангенс в маткаде

Этот раздел описывает тригонометрические, гиперболические и показательные функции Mathcad вместе с обратными им. Здесь также описываются встроенные функции Бесселя.

Тригонометрические функции и обратные им.

Тригонометрические функции Mathcad и обратные им определены для любого комплексного аргумента. Они также возвращают комплексные значения везде, где необходимо. Результаты для комплексных значений вычисляются с использованием тождеств:

Для применения этих функций к каждому элементу вектора или матрицы используйте оператор векторизации.

Обратите внимание, что все эти тригонометрические функции используют аргумент, выраженный в радианах. Чтобы перейти к градусам, используется встроенная единица deg. Например, чтобы вычислить синус 45 градусов, введите sin(45*deg).

Имейте в виду, что из-за ошибок округления, свойственных машинной арифметике, Mathcad может возвращать очень большое число в той точке, где находится особенность вычисляемой функции. Вообще, необходимо быть осторожным при вычислениях в окрестности таких точек.

asin(z)	Возвращает угол (в радианах), чей синус — z.
acos(z)	Возвращает угол (в радианах), чей косинус — z.
atan(z)	Возвращает угол (в радианах), чей тангенс — z.

Гиперболические функции sinh и cosh определяются формулами:

Эти функции также могут использовать комплексный аргумент и возвращать комплексные значения. Гиперболические функции тесно связаны с тригонометрическими функциями. Справедливы формулы:

sinh(iz)=isin(z)cosh(iz)=cos(z)

sinh (z)	Возвращает гиперболический синус z.
cosh (z)	Возвращает гиперболический косинус z.
tanh (z)	Возвращает sinh(z)/cosh(z), гиперболический тангенс z.
csch (z)	Возвращает 1/sinh(z), гиперболический косеканс z.
sech (z)	Возвращает 1/cosh(z), гиперболический секанс z.
coth (z)	Возвращает 1/tanh(z), гиперболический котангенс z.
asinh (z)	Возвращает число, чей гиперболический синус — z.
acosh (z)	Возвращает число, чей гиперболический косинус — z.
atanh (z)	Возвращает число, чей гиперболический тангенс — z.

Логарифмические и показательные функции

Логарифмические и показательные функции Mathcad могут использовать комплексный аргумент и возвращать комплексные значения. Значения экспоненциальной функции для комплексного аргумента вычисляются с применением формулы

e x+iy =e x (cos(y) + isin(y))

Вообще говоря, значения натурального логарифма даются формулой

ln(x + iy)=ln|x + iy|+ atan(y/x)i + 2n p i

В Mathcad функция ln возвращает значение, соответствующее n = 0. А именно:

ln(x + iy)=ln|x + iy|+ atan(y/x)i

Оно называется основным значением логарифма. Рисунок 1 иллюстрирует некоторые основные свойства логарифма.

exp(z)	Возвращает e в степени z.
ln(z)	Возвращает натуральный логарифм z. (z0).
log(z)	Возвращает логарифм z по основанию 10. (z0).

На Рисунке 1 показано, как можно использовать эти функции для вычисления логарифма по любому основанию.

Рисунок 1: Использование логарифмических функций.

Эти функции обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям.

Функции Бесселя первого и второго рода, J_n(x) и Y_n(x), являются решениями для дифференциального уравнения

Модифицированные функции Бесселя первого и второго рода, I_n(x) и K_n(x), являются решениями для немного видоизмененного уравнения:

J0(x)	Возвращает J0(x); x вещественный.
J1(x)	Возвращает J1(x); x вещественный.
Jn(m, x)	Возвращает Jn(x); x вещественный, 0m100.
Y0(x)	Возвращает Y0(x); x вещественный, x > 0.
Y1(x)	Возвращает Y1(x); x вещественный, x > 0.
Yn(m, x)	Возвращает Yn(x). x > 0, 0m100
I0(x)	Возвращает I0(x); x вещественный.
I1(x)	Возвращает I1(x); x вещественный.
In(m, x)	Возвращает In(x); x вещественный, 0m100.
K0(x)	Возвращает K0(x); x вещественный, x > 0.
K1(x)	Возвращает K1(x); x вещественный, x > 0.
Kn(m, x)	Возвращает Kn(x). x > 0, 0m100

Следующие функции возникают в широком круге задач.

x должен быть вещественным. G (z) Возвращает значение эйлеровой гамма-функции в z. Для вещественного z значения этой функции совпадают со следующим интегралом:

Гамма-функция Эйлера удовлетворяет рекуррентному соотношению

Откуда следует для положительных целых z:

Интеграл ошибок часто возникает в статистике. Он может также быть использован для определения дополнения интеграла ошибок по формуле:

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Научная электронная библиотека

Левинсон Л М, Габдрахманова К Ф, Зиганшин С С,

1.5. Некоторые стандартные функции MathCAD

Рассмотрим некоторые стандартные функции системы MathCAD. Введем специальные обозначения для аргументов функций. Пусть первый символ имени аргумента обозначает его тип:

M – квадратная матрица;

V – вектор (матрица из одного столбца);

A – произвольная матрица;

S – симметричная матрица;

G – произвольная матрица или число;

X – вектор или число;

Z – комплексная матрица или число;

z – комплексное число;

прочие символы – скалярные величины.

Экспоненциальные и логарифмические функции

exp(X) – экспонента от X;

ln(X) – натуральный логарифм от X;

log(X) – десятичный логарифм от X;

log(X,b) – логарифм от X по основанию b.

Гиперболические и тригонометрические (прямые и обратные) функции

sin(X), cos(X), tan(X), cot(X), sec(X), csc(X) – соответственно синус, косинус, тангенс, котангенс, секанс, косеканс от X, причем аргументы указываются в радианах;

sinh(X), cosh(X), tanh(X), coth(X), sech(X), csch(X) – аналогичные гиперболические функции;

asin(z), acos(z), atan(z), acot(z), asec(z), acsc(z) – соответственно арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс от z.

Функции для работы с комплексными числами

Re(Z), Im(Z) – соответственно вещественная и мнимая части комплексного числа Z;

arg(z) – аргумент комплексного числа z (в радианах).

length(V) – возвращает число элементов вектора V;

cols(A) – возвращает число столбцов матрицы A;

rows(A) – возвращает число строк матрицы A;

matrix(m, n, f) – матрица размером mxn, значения элементов матрицы определяются f – функцией f (i, j) от двух переменных (номера строки и номера столбца). Эта функция должна быть предварительно определена пользователем;

identity(n) – единичная матрица n×n;

tr(M) – след матрицы M (сумма элементов главной диагонали);

rank(A) – ранг матрицы M;

norme(M) – эвклидова норма матрицы M, то есть корень квадратный из суммы квадратов всех элементов;

eigenvals(M) – вектор, элементы которого являются собственными числами матрицы M;

eigenvecs(M) – матрица, состоящая из нормализованных собственных векторов матрицы M;

cholesky(S) – возвращает нижнетреугольную матрицу L – результат разложения Холецкого вида L∙LT = S;

lu(M) – возвращает матрицу размера n×3n, состоящую из трех соединенных матриц P, L, U, являющихся результатом LU-разложения вида P∙M = L∙U.

Пример вычислений с матричными функциями: нахождение собственного числа путем решения матричного уравнения det(M – λE) = 0 и с помощью функции eigenvals.

Элементы статистического анализа данных

gmean(G1,G2,G3…) – среднее геометрическое аргументов;

mean(G1,G2,G3…) – среднее арифметическое аргументов;

stdev(G1,G2,G3…) – среднеквадратичное отклонение.

fft(V1), ifft(V2) – прямое и обратное быстрые преобразования Фурье над вещественными данными. V1 – вектор из 2m элементов, V2 – вектор из 1 + 2m–1 элементов, m > 2;

cfft(A), icfft(A) – прямое и обратное преобразования Фурье над вещественными и комплексными векторами и матрицами;

wave(V), iwave(V) – прямое и обратное вейвлет-преобразования, V – вектор из 2m элементов, m – целое число.

Аппроксимация, интерполяция и экстраполяция

Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные.

Интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним).

Экстраполяция – определение наиболее правдоподобных последующих значений на основании анализа предыдущих значений (предсказание дальнейшего поведения неизвестной функции).

Применяются следующие функции MathCAD:

interp(VS,VX,VY,x) – возвращает интерполированное значение неизвестной функции при значении аргумента x. VS – вектор значений, который вернула функция regress. VX,VY – те же данные, что и для regress. Функции interp и regress используются в паре;

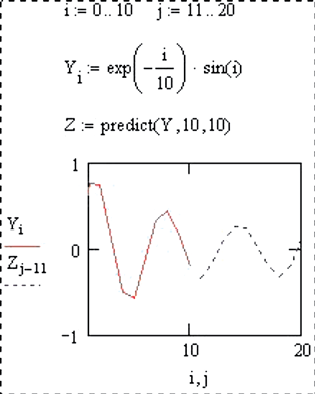
predict(V,m,n) – возвращает вектор из n предсказанных значений на основании анализа m предыдущих значений из вектора V. Предполагается, что значения функции в векторе V были получены при значениях аргумента, взятых последовательно, с одинаковым шагом. Используется алгоритм линейной предикции. Наиболее целесообразно использовать predict для предсказания значений по данным, в которых отмечены колебания.

Для интерполяции система MathCAD использует подход, основанный на применении метода наименьших квадратов.

Примеры интерполяции и экстраполяции:

1.5.1. Пусть заданы координаты пяти точек (1; 1), (2; 2), (3; 3), (4; 2), (5; 3), представляющих результаты измерения значений некоторой неизвестной функции при различных значениях x. Необходимо подобрать интерполирующую функцию (гладкую кривую), проходящую через заданные точки.

1.5.2. Дана функция y(i) = e–i/10∙sin (i). Известны значения данной функции при i = 0, 1, …, 10. Основываясь на десяти последних значениях, необходимо предсказать последующие десять значений.

Решения показаны на рис. 19.

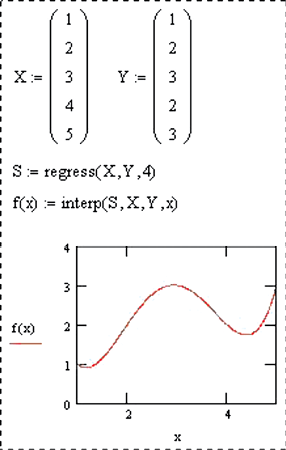
Рис. 19. Решения в MathCAD первой (а) и второй (б) задач

Нахождение корней полинома

max(G1,G2,…) – максимальное значение среди аргументов;

min(G1,G2,…) – минимальное значение среди аргументов;

if(a,b,c) – возвращает b, если a ≠ 0, иначе возвращает c;

sign(a) – возвращает –1, 0 или 1 в зависимости от знака числа a.

На рис. 20 показан пример применения функции if.

Источник

Как записать ctg в mathcad

Иллюстрированный самоучитель по MathCAD 11

Тригонометрические функции – Trigonometric.

Аргумент тригонометрических функций и результат обратных тригонометрических функций выражаются в радианах. Чтобы использовать значение угла в градусах, его необходимо перевести в радианы (листинг 10.6). Аргумент тригонометрических функций может быть комплексным.

Листинг 10.4. Примеры тригонометрических функций:

Листинг 10.5. Примеры расчета угла между прямой и осью OX:

Листинг 10.6. Расчет тригонометрических функций в градусах:

Арккотангенс

Не могу обозначить арккотангенс
Не могу найти ошибку. По калькулятору считает по-другому (на калькуляторе, при х=7 z=6.853, а в.

Записать арккотангенс в с++ билдере
Помогите записать уравнение на синтаксисе с++. Никак не могу разобраться с арккотангенсом, нашел.

Вычислить арккотангенс путем разложения в ряд
Помогите сделать пример. \text(x)=\frac

Сообщение было отмечено Mustang707 как решение

Как записать ctg в mathcad

Чтобы легче было понять написанное здесь, рекомендуется при первом чтении опускать содержимое скобок (точнее, текст в скобках), при втором чтении — текст в двойных скобках и т.д. Развернуть страничку во весь экран можно по ссылке в конце странички.

Иногда авторы в книгах используют выражение как имя переменной (синтаксис не позволяет этого делать, так как слева от оператора присваивания может быть либо имя переменной, либо имя функции от переменной), для этого в седьмой версии Маткада введена фитча «выражение как имя переменной», которая включается комбинацией клавиш Ctrl+Shift+O (в последующих версиях заменена комбинацией Ctrl+Shift+J). При нажатии этой комбинации, когда курсор стоит на чистом месте или в математической формуле, появляется плэйсхолдер в квадратных скобках. В этих скобках можно писать любую ахинею, и компьютер будет её считать именем переменной (при этом главное не перепутать одну ахинею с другой). Кстати, фонттаги у переменных при этом Маткад не различает. В справке по «Маткаду» это называется «химический режим».

Часто (практически всегда) авторы книг по электротехнике, ТЭЦ, статистической радиофизике используют неудачное обозначение комплексной передаточной функции: H(jω) (имея в виду при этом H(j·ω), так как переменной величиной является ω и поэтому слева от оператора присваивания под знаком функции должна быть та же переменная, иначе просто нужная функция не определится; например, если написать такое опрелеление: H(jω) := Q(j·ω), где Q(x) — дробно-рациональная функция от «x», то есть «правильное» выражение, то тогда Маткад выдаст сообщение об ошибке: простая переменная ω не определена. Если ей присвоить какое-нибудь значение, то тогда определится постоянная функция, значение которой будет зависеть от присвоенного значения ω и вида функции Q(x). А если написать определение: H(j·ω) := Q(j·ω), то тогда компьютер выдаст сообщение об ошибке «cannot be defined», так как, согласно синтаксису Маткада, слева от оператора присваивания может быть только имя переменной или имя функции от переменной; никакие выражения слева от оператора присваивания недопустимы. Чтобы определить комплексную функцию, никаких дополнительных мер принимать не нужно, комплексная функция может иметь точно такое же имя, как и действительная, и без всяких дополнительных символов, которые рисуют в книжках, например, «звёздочки», «чёрточки» над или под именем переменной. В приложении Маткад это не предусмотрено. Как говорится, «дурной пример заразителен» или ещё «одна кобыла всех сманила». Интересно, кто был первой кобылой? Котельников? Или Шеннон? Или генерал-майор Тихонов Василий Иванович (преподаватель ВВИА им. Жуковского)? Бумага конечно всё стерпит, но компьютер ругается матерно.

Кстати о комплексных числах и о их вычислении «вручную» и на компьютере. С комплексными числами «Маткад» обращается также легко, как с действительными. Даже имена комплексных переменных могут ничем не отличаться от имён действительных переменных. Только ответ он выводит всегда в алгебраической форме (в виде «a + 1j·b», где a и b — действительные числа. Цифра 1 слева от буквы j рисуется интерфейсом, если выделить соответствующий математический регион. Если выделение региона снять, то «1» не рисуется, а буква «j» сдвигается влево, так что образуется пробел между буквой «j» и символом умножения в седьмой версии Маткада. В последних версиях при выделении такого региона его длина увеличивается, а при снятии выделения уменьшается обратно, так что никаких пробелов не образуется. На распечатках никогда не бывает выделенных регионов, так что на распечатке комплексные числа имеют вид «a + j ·b» или «a + j·b»). Если в задаче требуется подробно расписать вычисления комплексных чисел, то нужно их перед сложением или вычитанием перевести в алгебраическую форму (если они имели показательную форму, например после умножения или деления или по условию задачи), а перед умножением или делением — соответственно в показательную (если они имели алгебраическую форму, например после сложения или вычитания или по условию задачи). Для вычисления функций от комплексных чисел существуют специальные формулы, в которые входят по отдельности действительная и мнимая части комплексного числа. Например:

exp(z) = exp(x + i·y) = e x + i·y = e x ·(cos(y) + i·sin(y)) = exp(x)·(cos(y) + i·sin(y))

Некоторые функции в приложении «Маткад» обозначаются не так, как в российской/советской литературе; например для тангенса вместо tg — tan, для арктангенса вместо arctg — atan, для функции e x предусмотрено более удобное обозначение exp(x) (можно использовать любое из них, но символический оператор вывода всегда возвращает функцию exp(x)). Особенно оно удобно, когда под знаком функции «экспонента» стоит дробь. Все функции с различными обозначениями приведены в таблице соответствия:

Кроме перечисленных здесь функций в «Маткаде» имеется огромное количество других функций, недоступных «фраерам дешёвым» (безлошадным крестьянинам): специальные функции (гамма-функция, все функции Бесселя, функция ошибок (функция Лапласа), около 20 стандартных распределений вероятности — дифференциальных, интегральных, обратных к ним и соответствующих им генераторов случайных чисел); всевозможные векторные и матричные функции; статистические функции — построение гистограммы и уравнения прямой регрессии и т.п.; функции чтения из файла и функции записи в файл (таблиц, растровых изображений в различных форматах, звуков); функции (процедуры) решения дифференциальных уравнений, как обыкновенных, так и в частных производных; функции решения уравнений и систем уравнений, функция решения задачи линейного и нелинейного программирования.
При решении задач по теории вероятностей иногда используется функция Лапласа Ф(x). В американской литературе (и соответственно в пакете «Маткад») вместо неё используется функция ошибок erf(x). Между этими функциями существует простая функциональная зависимость: Ф(x) = erf(x/sqrt(2)) или erf(x) = Ф(sqrt(2)·x). Первое уравнение используется для определения функции Лапласа. Можно определить функцию Лапласа с помощью степенного ряда, но тогда компьютер будет вычислять её гораздо дольше и с гораздо меньшей точностью и при x > 5 вообще неверно. Графики этих функций изображены в левом верхнем фрейме (если у вас эта страница не развёрнута во весь экран). Если у Вас рисунки в этот фрейм тоже почему-то не загружаются, то ссылку на этот рисунок я вставил прямо здесь:

Чтобы использовать русские обозначения функций, нужно их определить вначале файла (или сделать ссылку на файл, в котором эти функции определены), например:

tg(x) := tan(x); ctg(x) := tan(x) –1 ; arcsin(x) := asin(x); arccos(x) := acos(x);

ch(x) := 0.5·(exp(x) + exp(–x)); sh(x) := 0.5·(exp(x) – exp(–x))

Arsh(x) := ln(x + sqrt(x 2 + 1)); Arch(x) := ln(x ± sqrt(x 2 – 1)) — «длинный логарифм».

Ссылка на файл имеет вид: Reference:»[буква диска]:\[полный путь файла]\[имя файла.mcd]» (пиктограмма ссылки, показываемая на экране, на распечатке отсутствует). Чтобы не распечатывать определения функций с русскими именами, также можно их определить «за кадром», то есть справа от вертикальной черты, показывающей границу печати (в файле шаблона, который открывается для создания нового файла, в настройках печати у меня стоит галка напротив «print to right margin» — печатать до правой кромки; эта настройка переходит на все новые фалы, основанные на этом шаблоне).

Если задача приводится в нескольких вариантах, которые отличаются только цифрами, то я пишу файл сразу на все эти варианты таким образом, что нужно только подставить значение простой переменной, соответствующей номеру варианта, а компьютер сам автоматически выбирает нужные данные для расчёта. При этом не нужно переписывать все табличные данные, а только свои, которые выводятся с помощью операторов вывода после слова » Дано: «.

Хотя «Маткад» позволяет выполнять действия не только над «голыми» числами, но и над размерными числами — значениями той или иной физической величины с соответствующей единицей измерения и автоматически определять размерность полученного ответа (выражая его через основные единицы измерения физических величин: кг, м, с, Кл (или А), К, моль, лм), но использует он при этом английские обозначения (kg, m, s, coul (A), K, mole, cd, sr). Чтобы он выражал ответы через русские обозначения основных физических величин, нужно ввести их названия в диалоге, который вызывается через меню math, options, закладка dimensions. Поставить галку «display dimensions» и ввести краткие русские обозначения основных физических величин. Чтобы не делать это каждый раз, у меня написан специальный файл, который сохранён в виде специального шаблона («имя_файла.mct»). Также написан специальный файл, в котором определены имена единиц измерения производных физических величин и всех кратных единиц, некоторых внесистемных единиц и основных физических постоянных, операторы для перевода из градусов в радианы и обратно и операторы перевода температуры из шкалы Цельсия в шкалу Кельвина и обратно. Заодно определены русские обозначения функций, которые в американской литературе имеют другое обозначение. Ссылка на этот файл имеет вид:

Reference:C:\Задачи\физика\единицы и константы.mcd Размер файла 21186 байт.

В некоторых задачах по техническим предметам, в которых единицы измерения не существенны, а набор их невелик и заранее известен (например, по кинематике — время, координата, скорость и ускорение или ТММ — также угол поворота, угловая скорость и угловое ускорение) вместо единиц измерения физических величин применяется их профанация (то есть определяются безразмерные простые переменные с именами, как у единиц измерения ФВ), например:

м:=1 с:=1 м/с:=1 м/с^2:=1 рад:=1 рад/с:=1 рад/с^2:=1

чтобы можно было их подставлять в плэйсхолдер ответа в регион с оператором вывода (чтобы ответы были не пустые числа, а с соответствующими единицами измерений). Так как единицы измерения в таких задачах совершенно не существенны, то можно определить любые другие, например, см:

Этот способ употребления единиц измерения в ответах используется для того, чтобы без крайней необходимости не применять ссылку на файл «единицы и константы», так как «Маткад» при этом использует слишком много ресурсов компьютера (точнее говоря, начинает глючить независимо от объёма оперативной памяти), и если открыть несколько таких файлов (а также редактор WordPicture), то он начинает глючить со страшной силой. Например, векторные рисунки показывает в масштабе 400%, на «print preview» («просмотр пред печатью») содержимое страницы выходит за её пределы, если выделить несколько регионов и попытаться их перенести с помощью мышки, то они оказываются в начале файла и наконец, интерфейс перестаёт частично или полностью перерисовывать содержимое окна редактируемого файла, так что вместо нужного файла он рисует другой файл или другое приложение, или рабочий стол (если заглючивший файл не закрыть и не переключиться на другой, а окно «Маткада» свернуть, а затем снова развернуть).

При «ручных» вычислениях часто выполняются подразумеваемые действия, для которых не предусмотрено (в литературе) вообще никаких имён функций, например, округление. Если мы хотим написать файл, который автоматически выполнял бы такие действия для любых исходных данных, в этом случае необходимо применять специальные функции. Например, функция округления до ближайшего большего целого числа имеет имя ceil(x), а а до ближайшего меньшего целого — floor(x). Если требуются более сложные виды округлений, то тогда необходимо определить соответствующую функцию, выраженную через функции ceil(x) и(или) floor(x) или через функцию if([условие], f1(x), f2(x)). Пример: требуется округлить ответ до ближайшего целого количества миллиметров в большую сторону. Тогда функция округления будет иметь вид:

Функции выбора максимальной или минимальной величины из нескольких «max» и «min» соответственно в советской/российской литературе считаются функциями нескольких скалярных переменных, а в американской — функции одной векторной или даже матричной переменной. Поэтому, прежде чем использовать эти функции, нужно определить соответствующий вектор:

Если в задании какая-то (непрерывная) функция задана таблицей и мы хотим, чтобы компьютер автоматически вычислял значения этой функции даже в промежуточных точках и при этом с достаточно высокой точностью, то можно применить встроенную в «Маткад» процедуру кубической интерполяции (сплайнами — отрезками кубических полиномов по обеим переменным). Синтаксис этой процедуры имеет вид:

S := cspline(X,Y) f(x) := interp(S,X,Y,x)

где вектор X — значения переменных в таблице, вектор Y — соответствующие значения функции.

При этом бывает 3 вида кубической интерполяции: с кубическими концами (оператор «cspline«), с параболическими концами (третья производная равна нулю на концах интервала интерполяции (первый и последний элементы вектора X; оператор «pspline«) и линейными концами (третья и вторая производные равны нулю на концах интервала интерполяции; оператор «lspline» соответственно).

По некоторым предметам (особенно по теплотехнике) авторы методичек записывают формулы в таком виде, чтобы ответ получался сразу во внесистемных единицах, без дополнительных вычислений и преобразований. На компьютере это недопустимо, если использовать единицы измерения физических величин, так как по умолчанию предполагается, что ответ должен получиться в стандартных единицах. А если определить внесистемную единицу с соответствующим численным значением и подставить её в плэйсхолдер ответа, то компьютер разделит ответ на её численное значение и ответ будет неправильным. Даже если использовать профанацию единиц измерения, то нелогично было бы присваивать единичное значение внесистемным единицам, например:

кг/ч := 1 или кг/кВт·ч := 1

Если мы захотим узнать величину ответа в системных единицах, то тогда их придётся определить следующим способом:

кг/с := 3600 или кг/Дж := 3600000

А если эти вычисления входят в последующие формулы, да ещё в единицах «СИ», то тогда уж лучше исправить формулы и единицы измерения определить соответственно их численному значению, а ответ во внесистемных единицах компьютер сам вычислит, если подставить эту единицу в плэйсхолдер ответа (региона с оператором вывода численного значения соответствующей переменной.)

Иногда в литературе формулы даются не в системе «СИ», а в какой-нибудь другой, например в книге «Сивухин Д. В., «Общий курс физики», т.5, «Основы квантовой механики и атомная физика»» формула для вычисления постоянной Ридберга (а также все остальные) даются в системе СГС. В этом случае я сам переписываю формулы в нужном виде, чтобы можно было пользоваться приложением «Маткад».

Ниже приводятся примеры того, как выглядит распечатка, и как её надо переписывать. (Пока не приводятся :-))

Источник