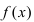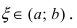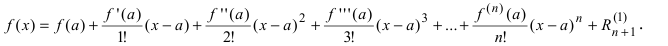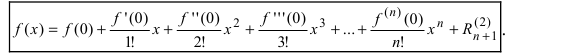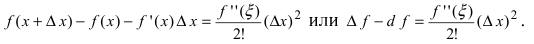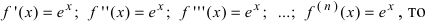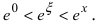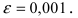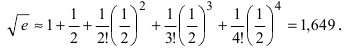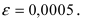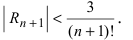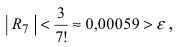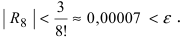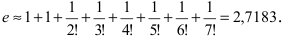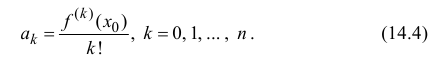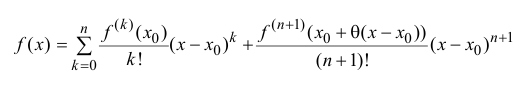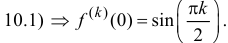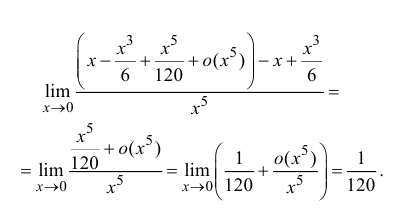Формула Тейлора и ее применение с примерами решения
Содержание:
Формула Тейлора и ее применение
Формула Тейлора
Теорема: Если функция
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора 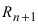
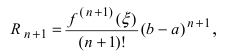
В этой формуле неизвестной является только величина 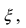
При a = 0 формула Тейлора переходит в формулу Маклoрена:
Пример:
Представить по формуле Маклорена функцию 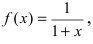
Решение:
Вычислим три первых производных заданной функции:
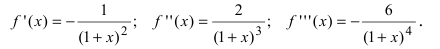
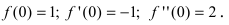
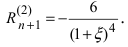
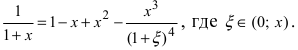
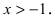
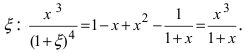
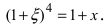
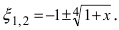
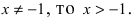
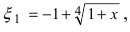
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:
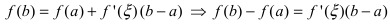
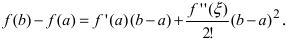
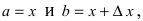
Применение формулы Тейлора
Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 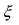
Пример:
Представить функцию 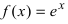
Решение:
Так как 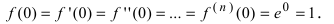
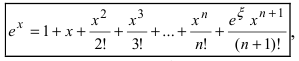
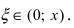
Пример:
Вычислить 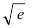
Решение:
Так как основание 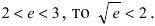
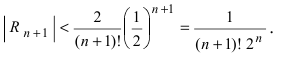
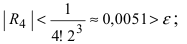
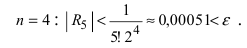
Пример:
Вычислить число е с точностью
Решение:
Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа
При n = 6 имеем
при n = 7 получаем
Итак,
Если вычислять значение числа е с точностью 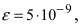
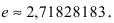
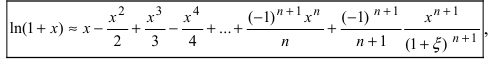
Пример:
Вычислить 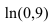
Решение:
Формула тейлора
Пусть функция y=f(x) дифференцируема в точке 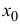
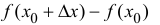
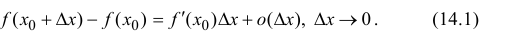
Пусть 
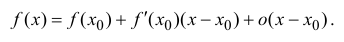
Рассмотрим многочлен 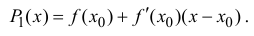
Многочлен 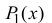
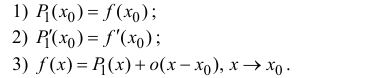
Пусть функция y=f(x) n раз дифференцируема в точке 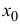
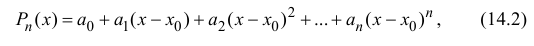
обладающий аналогичными свойствами: 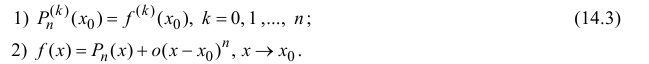
Из (14.2), (14.3) следует, что 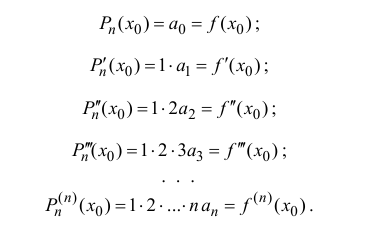
Поэтому коэффициенты 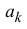
Далее 
Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 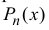
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке 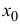
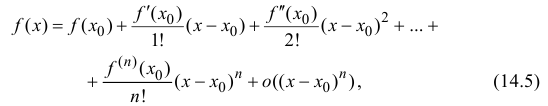
где 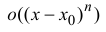
малости, чем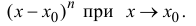
Формула (14.5) называется формулой Тейлора, многочлен 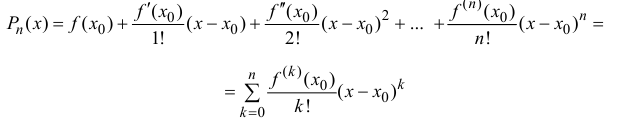
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности 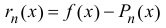
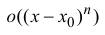
Если функция 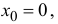
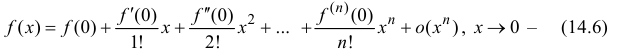
формула Маклорена.
Если функция 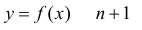
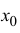
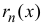
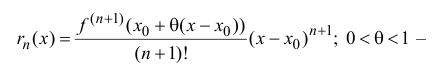
называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.
Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений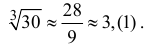
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа: 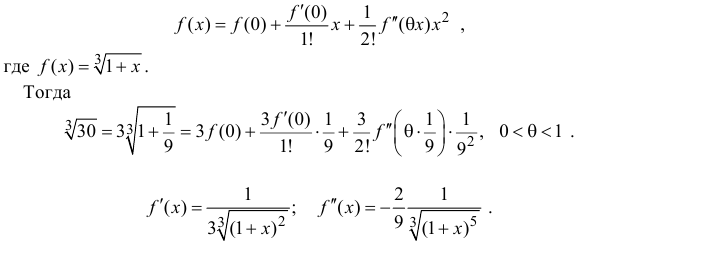
Поэтому
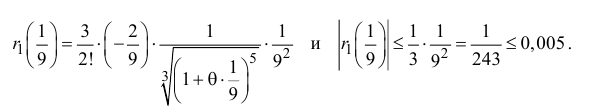
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.
Пример 14.2
Запишем формулу Маклорена n-го порядка для функции y=sin x: 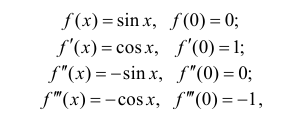
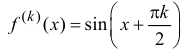
Таким образом, 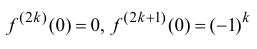
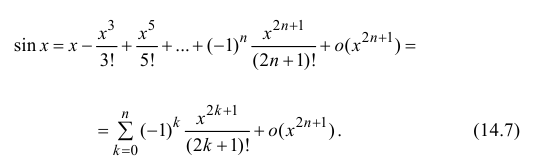
Аналогично 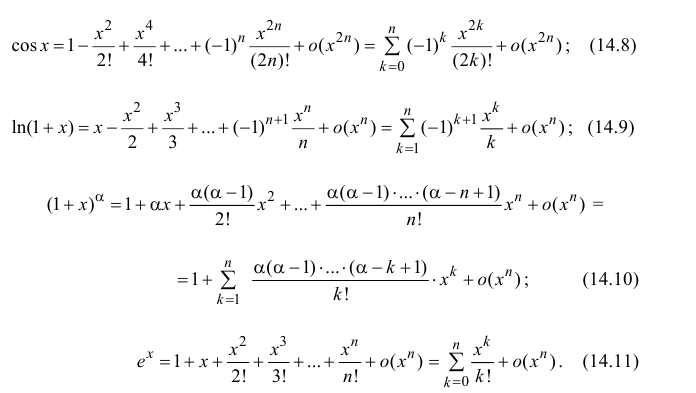
Формулы (14.7)–(14.11) называются основными разложениями.
Пример 14.3
Разложить 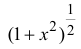
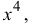
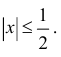
Решение
Пусть 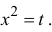
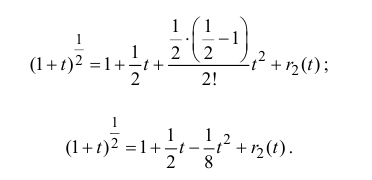
Остаточный член запишем в форме Лагранжа: 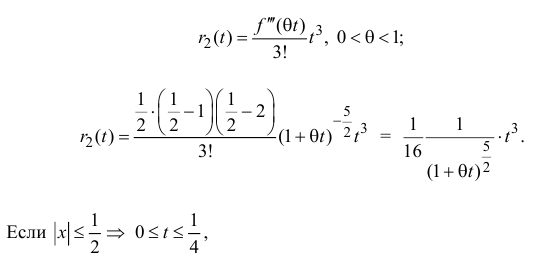
поэтому 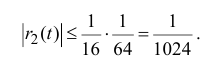
Таким образом, 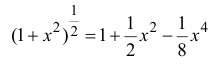
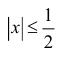
Пример 14.4
Найти 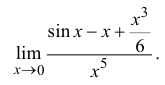
Решение
Воспользуемся разложением (14.7): 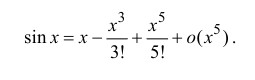
Тогда
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Формула Тейлора
Формула Тейлора с остаточным членом в форме Лагранжа.
Если функция \(f(x)\) имеет в точке \(x_<0>\) производную n-го порядка, то существует многочлен \(P_
$$
P_n(x_0)=f(x_<0>),\ P_
$$
Этот многочлен представляется в виде
$$
P_n(x)=f(x_<0>)+\frac
$$
\(\circ\) Пусть \(\varphi(x)=(x-x_0)^m\), где \(m\in\mathbb
$$
\varphi^<(k)>(x_<0>)=\left\<\begin
0, & если \ k\neq m,\\
k!, & если \ k=m.
\end
$$
Из \eqref
Пусть функции \(f(x)\) и \(\psi(x)\) определены в \(\delta\)-окрестности точки \(x_0\) и удовлетворяют следующим условиям:
Тогда для каждого \(x\in\dot_<\delta>(x_<0>)\) существует точка \(\xi\), принадлежащая интервалу с концами \(x_0\) и \(x\) такая, что
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi^<(n+1)>(\xi)><\psi^<(n+1)>(\xi)>.\label
$$
\(\circ\) Пусть, например, \(x\in(x_0,x_0+\delta)\). Тогда, применяя к функциям \(\varphi\) и \(\psi\) на отрезке \([x_0,x]\) теорему Коши и учитывая, что \(\varphi(x_0)=\psi(x_0)=0\) в силу условий \eqref
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi(x)-\varphi(x_0)><\psi(x)-\psi(x_0)>=\frac<\varphi'(\xi_1)><\psi'(\xi_1)>\quad x_0 Теорема 1.
Пусть существует \(\delta >0\) такое, что функция \(f(x)\) имеет в \(\delta\)-окрестности точки \(x_0\) производные до \((n+1)\)-го порядка включительно.
Тогда для любого \(x\in\dot_\delta(x_0)\) найдется точка \(\xi\), принадлежащая интервалу \(\Delta\) с концами \(x_<0>\) и \(x\), такая, что
$$
f(x)=f(x_0)+\frac
$$
\(\circ\) Пусть \(x\in\dot_\delta(x_0)\), \(P_n(x)=\displaystyle \sum_
$$
r_
$$
Так как многочлен \(P_
$$
r_n(x_0)=r_n'(x_0)=\ldots=r_
$$
Рассмотрим функции \(\varphi(x)=r_n(x)\), \(\psi(x)=(x-x_0)^
$$
\frac<\varphi(x)><\psi(x)>=\frac
$$
так как \(P_n^<(n+1)>(x)\equiv 0,\ \psi^<(n+1)>(x)=(n+1)!\) Из равенств \eqref
Функцию \(r_n(x)=\displaystyle \frac
Если функции \(\varphi\) и \(\psi\) дифференцируемы \(n\) раз при \(x\geq x_<0>\) и удовлетворяют условиям \(\varphi^<(k)>(x_<0>)=\psi^<(k)>(x_<0>)\), \(k=\overline<0,n-1>\), \(\varphi^<(n)>(x)>\psi^<(n)>(x)\) при \(x > x_0\), то \(\varphi(x) > \psi(x)\) при \(x > x_<0>\).
\(\circ\) Для \(n=1\) утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим \(f(x)=\varphi(x)-\psi(x)\). Тогда \(f^<(k)>(x_<0>)=0\) при \(k=\overline<0,n-1>0\), и по формуле \eqref
$$
f(x)=\frac<1>
$$
Если \( x> x_<0>\), то \(\xi > x_0\), \(f^<(n)>(\xi)=\varphi^<(n)>(\xi)-\psi^<(n)>(\xi) > 0\), и поэтому \(f(x) > 0\), то есть \(\varphi(x) > \psi(x)\) при \(x > x_<0>\). \(\bullet\)
Формула Тейлора с остаточным членом в форме Пеано.
Из существования \(f^<(n)>(x_0)\) следует, что функция \(f(x)\) определена и имеет производные до \((n-1)\)-го порядка включительно в \(\delta\)-окрестности точки \(x_0\). Обозначим \(\varphi(x)=r_n(x)\), \(\psi(x)=(x-x_0)^n\), где функция \(r_n(x)\) определяется формулой \eqref
$$
\frac
$$
где \(\xi=\xi(x)\) и
$$
x_0 Замечание 2.
Формулу \eqref
Разложить функцию \(f(x)\) по формуле Тейлора в окрестности точки \(x_0\) до \(o((x-x_0)^n)\) — значит представить ее в виде \eqref
\(\circ\) По теореме 2 справедлива формула \eqref
$$
a_0+a_1(x-x_0)+\ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\\=f(x_<0>)+f'(x_<0>)(x-x_0)+\ldots+f^<(n)>(x_<0>)\frac<(x-x_<0>)^
$$
Переходя к пределу при \(x\rightarrow x_<0>\) в равенстве \eqref
$$
a_1+a_2(x-x_0)+\ldots+a_n(x-x_0)^
$$
Переходя в этом равенстве к пределу при \(x\rightarrow x_0\), находим \(f'(x_<0>)=a_<1>\). Продолжая эти рассуждения, получаем равенства \eqref
Теорема 3 означает, что представление в виде \eqref
Разложить функцию \(\displaystyle \frac<1><1-x>\) по формуле Тейлора в окрестности точки \(x_<0>=0\) до \(o(x^
\(\triangle\) Воспользуемся равенством \((1+x+\ldots+x^
$$
\frac<1><1-x>=1+x+\ldots+x^n+o(x^n).\label
$$
Так как функция \(\displaystyle \frac<1><1-x>\) бесконечно дифференцируема при \(x\neq 1\) (имеет производные любого порядка), то по теореме 3 формула \eqref
Разложение основных элементарных функций по формуле Тейлора.
Если \(x_<0>=0\) и существует \(f^<(n)>(0)\), то равенство \eqref
$$
f(x)=\sum_
$$
Формулу \eqref
Пусть, функция \(f(x)\) бесконечно дифференцируема на интервале \((-l,l)\). Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции \(f\) выполняются условия \(f^<(2k)>(0)=0\), \(k\in\mathbb
Поэтому формулу \eqref
$$
f(x)=\sum_
$$
а для нечетной функции — в виде
$$
f(x)=\sum_
$$
В формуле \eqref
Показательная функция.
Гиперболические функции.
Так как \(\operatorname