Периметр
Периметр — это сумма длин всех сторон многоугольника.
Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».
Периметр измеряется в единицах длины: мм, см, м, км и т.д.
При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».
Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

PABCD = (AB + BC) · 2
PABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

PEKFM = 4 · KE
PEKFM = 4 · 7 = 28 (см)
Как найти периметр многоугольника
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

PABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)
Как найти периметр фигуры
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.
P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
Периметр многоугольника
Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.
В математике периметр обозначают буквой P (пэ).
Периметр прямоугольника
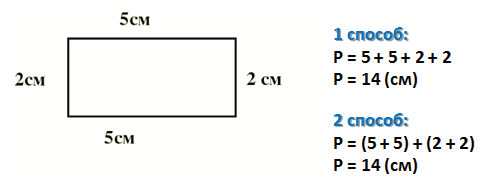
Например, найдём периметр данного прямоугольника.
Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.
Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.
Формула для подсчета периметра прямоугольника:
(a + b) • 2
a – длина прямоугольника
b – ширина прямоугольника.
Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:
Периметр треугольника
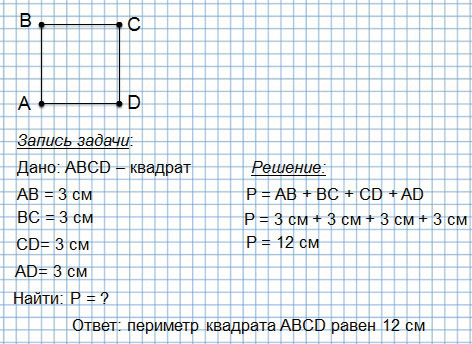
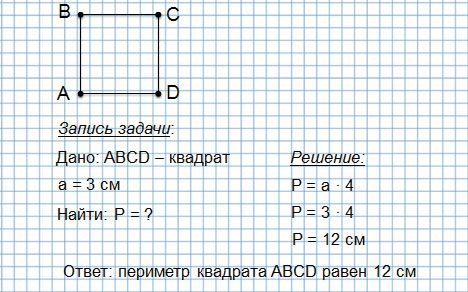
Периметр квадрата
Первый способ (когда мы еще не знаем действие умножения):
Второй способ (когда мы изучили действие умножения):
Поделись с друзьями в социальных сетях:
Формула расчета периметра многоугольника
Что такое периметр многоугольника
Периметр многоугольника в геометрии — это результат сложения длин всех его сторон.
Свойства многоугольника
Как вычислить периметр правильного многоугольника
Свойства правильного многоугольника
Формула
где a — длина стороны, n — количество сторон.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для неправильного многоугольника
Описание
У неправильного многоугольника все стороны разного размера.
Формула
Его периметр (P) можно рассчитать, сложив все длины его сторон (a, b, c,d и т.д.). Это первый способ.
Второй способ: если есть стороны с одинаковыми длинами, формулу можно сократить, использовав умножение.
Дан прямоугольник со сторонами 4см, 4см, 2см и 2см. Чтобы узнать периметр, можно просто их все сложить, как показано в формуле выше. А можно сделать так: 4×2+2×2, так как стороны попарно равны.
Этот способ подойдет и для фигур с большим количеством сторон, некоторые из которых равны.
Дан восьмиугольник со сторонами 5см, 5см, 3см, 3см, 3см, 2см и 1см. Периметр можно высчитать сложением, а можно считать так: 5×2+3×3+2+1.
По заданным координатам
Как начертить многоугольник
Формула для расчета периметра
Далее нужно находить длины всех получившихся сторон.
В формулу нужно подставить вместо x и y координаты сторон.
Примеры решения задач
Задания приведены разного уровня сложности. Расположены по принципу «от простого к сложному».
Во всех задачах нужно найти периметр фигур. Этот вопрос дублироваться в каждом примере ниже не будет.
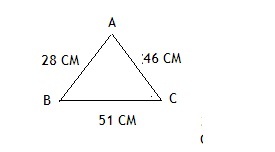
Пример 1
Дан треугольник ABC. AB=28см, BC=51см, AC=46см.
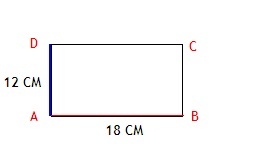
Пример 2
В прямоугольнике ABCD длина синей стороны 12 см, а красной 18 см.
Пример 3
Дан квадрат со стороной 12 см.
Мы знаем, что все стороны квадрата одинаковые. Их всего 4. Значит, P=12×4=48см.
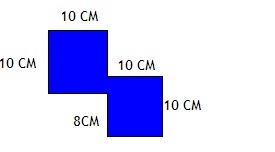
Пример 4
Дана фигура (данные на рисунке).
На рисунке мы видим восьмиугольник. У него шесть сторон по 10 см и две стороны по 8 см. Значит, P=10×6+8×2=60+16+76см.
Урок 27 Тема : ПЕРИМЕТР МНОГОУГОЛЬНИКА
Педагогические задачи: дать представление о периметре многоугольника; познакомить с понятием «периметр»; продолжать работу над задачами и выражениями изученных видов; формировать умение решать составные задачи выражением, сравнивать выражения.
Планируемые образовательные результаты:
Личностные: принимают и осваивают социальную роль обучающегося; имеют мотивацию к учебной деятельности; стремятся развивать внимание, память, мышление, навыки счета, навыки сотрудничества со сверстниками и со взрослыми; умеют аргументировать свою точку зрения; проявляют самостоятельность, личную ответственность.
Предметные: знают, что такое периметр многоугольника, виды многоугольников, устную и письменную нумерацию чисел в пределах 100, отличительные особенности задачи; умеют: находить периметр различных многоугольников, решать задачи изученных видов, соотносить задачи с данным решением и чертежом, решать задачи выражением, составлять и сравнивать числовые выражения.
Метапредметные (критерии сформированности/оценки компонентов УУД): регулятивные: формулируют учебную задачу урока, составляют план и последовательность действий; контролируют и оценивают, собственную деятельность и деятельность партнеров по образовательному процессу, при необходимости вносят корректировки; способны к саморегуляции; познавательные: формулируют познавательную цель, выделяют необходимую информацию; создают алгоритм деятельности; структурируют знания, анализируют объекты, сравнивают их, строят логическую цепочку рассуждений; коммуникативные: знают правила ведения диалога, достаточно полно и точно выражают свои мысли, уважают в общении и сотрудничестве всех участников речевого высказывания, при возникновении спорных ситуаций не создают конфликтов.
м етоды и формы обучения: частично-поисковый; индивидуальная, фронтальная, групповая
Наглядно-демонстрационный материал: многоугольники, домик со сменными окошками для устного счета.
Основные понятия и термины: периметр, многоугольники, сложить, вычесть, слагаемое, сумма, значение суммы, уменьшаемое, вычитаемое, разность, значение разности, задача, простая задача, составная задача, выражение, сравнить.
о рганизационная структура (сценарий) урока
I. Каллиграфическая минутка. – Рассмотрите числа, записанные на доске: 20 20 20 20 20 . 50 50 50 50 50 .
– Что вы заметили? Что можете сказать? – Пропишите числа в своих тетрадях.
II. Устный счет. 1. «Расшифруй и зашифруй». На доске записано задание 8 (с. 43).
Зашифрованы слова: кот, сова, вол.
салют – 21, 53, 25, 57, 29;
пакет – 23, 53, 55, 59, 29;
III. Подготовка к восприятию нового материала. Сообщение темы и целей. На магнитной доске расположены различные многоугольники:
– Что объединяет все фигуры? (Они все – многоугольники.)
– На какие группы вы бы разделили все изображенные многоугольники?
– Измерьте стороны четырехугольника АВСD (нарисован на доске).
– Запишем, чему равна каждая сторона.
Запись на доске и в тетрадях:
АВ = 2 см 5 мм СD = 2 см
– Запишем сумму всех сторон четырехугольника.
Запись на доске и в тетрадях:
– Найдите значение суммы. (2 см 5 мм + 3 см + 2 см + 5 см = 12 см 5 мм.)
– Слышали ли вы слово «периметр» раньше? Знаете ли, что оно означает?
– Сегодня на уроке вы узнаете, что такое периметр, будете находить периметры разных многоугольников, познакомитесь с различными способами нахождения периметра многоугольника.
IV. Открытие новых знаний.
Открывается закрытая доска (или проецируется слайд), на которой написано:
Периметр – это сумма длин всех сторон многоугольника.
– Кратко слово «периметр» записывается буквой Р – «пэ».
– Рассмотрите фигуры в задании 1 (с. 42). Назовите их.
– Измерьте стороны голубого четырехугольника.
– Как найти периметр данной фигуры? (Все стороны сложить.) Найдите его периметр.
– Найдите периметр зеленого четырехугольника. Что для этого следует сделать?
– Как найти периметр треугольника? Найдите его периметр.
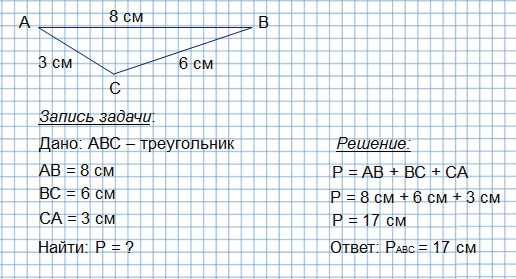
Затем подробно разбирается задача 2 (с. 42). Поскольку это геометрическая задача, то ее запись будет несколько отличаться от записи задач, которые учащиеся решали ранее. Прежде чем записать задачу, необходимо выполнить чертеж.
Дано: АВС – треугольник Решение :
ВС = 3 см Р тр = 8 см + 3 см + 6 см;
Р тр = 8 см + 3 см + 6 см;
Вместе по лесу идем, Расстилается ковер
Не спешим, не отстаем. И направо, и налево.
Вот выходим мы на луг. К небу руки протянули,
Тысяча цветов вокруг! Позвоночник растянули.
Вот ромашка, василек, Отдохнуть мы все успели
Медуница, кашка, клевер. И на место снова сели.
V. Работа над задачами.
– Прочитайте текст задачи 4 (с. 42). Что в задаче известно? Что следует узнать?
– Назовите данные и искомое число.
– Как бы вы решили эту задачу?
– Можно ли было эту же задачу решить по-другому? Как?
– Запишите любое из выражений, найдите его значение. Запишите ответ задачи.
Затем учащиеся читают текст задачи 5 (с. 43) и соотносят его с чертежом-схемой, приведенным ниже. После чего под руководством учителя составляется выражение, а затем формулируется и записывается ответ задачи.
VI. Работа с выражениями.
VII. Рефлексия учебной деятельности. – Какие открытия сделали на уроке? Что такое «периметр»? – Что бы вам хотелось выполнить еще? Как вы сегодня работали?