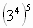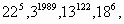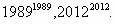Как получить последнию цифру числа!
Скажите пожалуйста как получить последнюю цифру числа!
Как получить последнию дату месяца?
Люди, подскажите, как расчитать последнию дату месяца?
Переставить последнию и первую цифру в числе
Как переставить последнию и первую цифру в числе местами? Используя for,if,while и никаких более.
Решение
Дано натуральное число n, переставить местами первую и последнию цифру местами.
№ 1: Дано натуральное число n, найти сумму первой и последней цифры этого числа. № 2: Дано.
Из двух чисел получить новое путём замены чётных цифр первого числа на наибольшую цифру второго числа
Условие: Разработать программу для реализации указанного действия над целыми числами без знака.
Из одного числа получить второе, заменив каждую цифру на единицу
Доброго времени суток. Недавно мне в голову пришла идея написать следующюю программу. Её смысл.
Получить первую цифру из дробной части положительного вещественного числа
Присвоить целой переменной k первую цифру из дробной части положительного вещественного.
Последняя цифра числа
Найдите последнюю цифру числа:
а) Заметим, что последняя цифра произведения двух натуральных чисел такая же, как последняя цифра произведения последних цифр этих двух чисел.
Пользуясь этим правилом, составим последовательность последних цифр степеней тройки: \[3,\, 9,\, 7,\, 1,\, 3,\, 9,\, 7,\, 1,\cdots\] Заметим, что в этой последовательности блоки по четыре цифры \(3,\ 9, \ 7, \ 1\) повторяются, значит, последняя цифра числа \(3^<33>\) зависит от того, какой остаток будет давать число \(33\) при делении на \(4\) (так как блоки по \(4\) цифры).
Последняя цифра суммы равна последней цифре суммы последних цифр исходных слагаемых.
Последняя цифра числа \(n^2\) равна \(4\) ( \(n\in\mathbb
Таким образом, предпоследняя цифра числа \(n^2\) обязательно чётна.
Таким образом, подходящих \(m\) и \(n\) не существует.
ЕГЭ по математике — одно из самых сложных тестирований для выпускников. Многолетняя практика показала, что очень часто ученики допускают неточности при вычислении последней цифры натурального числа. Данная тематика сама по себе довольно сложна, так как требует особой точности, внимательности и развитого логического мышления. Чтобы без проблем справиться с подобными заданиями, рекомендуем воспользоваться удобным онлайн-сервисом «Школково». На нашем сайте вы найдете все необходимое для решений уравнений на нахождение последней ненулевой цифры числа и подтяните знания в смежных тематиках.
Сдавайте Единый государственный экзамен на «отлично» вместе со «Школково»!
Наш образовательный портал построен таким образом, чтобы выпускнику было максимально удобно готовиться к итоговой аттестации. Сначала ученик обращается к разделу «Теоретическая справка»: вспоминает правила решения уравнений, освежает в памяти важные формулы, которые помогают найти последнюю цифру числа. После этого переходит в «Каталоги», где находит множество задач различных уровней сложности. Если с каким-либо упражнением возникают затруднения, его можно перенести в «Избранное», чтобы вернуться к нему позже и решить самостоятельно либо с помощью преподавателя.
Специалисты «Школково» собрали, систематизировали и изложили материалы по теме в максимально простой и понятной форме. Таким образом большое количество информации усваивается в короткие сроки. Школьники смогут выполнять даже те задания, которые совсем недавно вызывали у них большие трудности, в том числе и те, где необходимо указать несколько решений.
Чтобы занятия проходили максимально эффективно, рекомендуем начать с наиболее легких примеров. Если они не вызвали сложностей, не теряйте время — переходите к задачам среднего уровня, так вы определите свои слабые стороны, сделаете упор на наиболее сложные для вас задания и добьетесь больших результатов. После ежедневных занятий в течение 1―2 недель вы сможете за пару минут вывести даже последнюю цифру числа Пи. Данное задание достаточно часто встречается в ЕГЭ по математике.
База упражнений на нашем портале постоянно обновляется и дополняется преподавателями с большим стажем. У школьников есть отличная возможность каждый день получать совершенно новые задания, а не зацикливаться на одних и тех же примерах, как зачастую приходится делать при повторении по школьному учебнику.
Начните занятия на сайте «Школково» уже сегодня, и результат не заставит себя ждать!
Обучение на нашем портале доступно всем желающим. Чтобы вы отслеживали свой прогресс и получали новые задания, созданные персонально для вас, зарегистрируйтесь в системе. Желаем вам удачной подготовки!
Как написать последнюю цифру числа
При помощи операции нахождения остатка и целочисленного деления можно достаточно несложно вычислить любую цифру числа.
Рассмотрим программу получения цифр двузначного числа:
Результатом выполнения программы будут два числа:
То есть сначала мы вывели последнюю цифру числа, а затем первую цифру.
Рассмотрим программу получения цифр трёхзначного числа:
Результатом выполнения программы будут три числа:
То есть сначала мы вывели последнюю цифру числа, затем среднюю цифру, а затем первую цифру.
Решение задач
Задача 1. Напишите программу, определяющую число десятков и единиц в двузначном числе.
Решение. Число единиц – это последняя цифра числа, число десятков – первая цифра. Чтобы получить последнюю цифру любого числа, нужно найти остаток от деления числа на 10. Чтобы найти первую цифру двузначного числа, нужно поделить число нацело на 10. Программа, решающая поставленную задачу, может иметь следующий вид:
Задача 2. Напишите программу, в которой рассчитывается сумма цифр двузначного числа.
Решение. Программа, решающая поставленную задачу, может иметь следующий вид:
Задача 3. Напишите программу, которая печатает число, образованное при перестановке цифр двузначного числа.
Решение. Программа, решающая поставленную задачу, может иметь следующий вид:
Задача 4. Напишите программу, в которую вводится трёхзначное число и которая выводит на экран его цифры (через запятую).
Решение. Программа, решающая поставленную задачу, может иметь следующий вид:
Исследовательская работа «Ключ к угадыванию цифры»
Разделы: Математика
Основная часть
I. Нахождение последней цифры в записи степени натурального числа.
После изучения темы “Степень с натуральным показателем” была предложена такая задача: найти последнюю цифру степеней:
а) 
, 
, 
, 
, 
;
б) 
, 
.
Мы заметили, что в первом случае показатели степеней составные числа, а во втором случае показатели степеней простые числа. В обоих случаях есть основания четные и нечетные. Мы сначала попробовали представить степени в виде произведения степеней с тем же основанием и одинаковыми показателями, затем воспользовались со свойствами степеней с натуральными показателями
Например, = 
*
*
* 
или 
В ходе решения таких задач мы поняли, что
всегда оканчивается (при натуральном) n на 6.
Но вторая задача достаточно сложная, так как показатели степеней простые числа и мы не можем представить эти степени в виде произведения степеней с одинаковыми показателями, как делали раньше. Но мы нашли способы решения.
 =  *  * * *  | или  | ||||||
| 9 | 9 | 9 | 9 | 3 | 1 | 3 | |
 | 3 | ||||||
| 1 | 3 | 3 | |||||
| 3 | |||||||
Значит, последняя цифра степени равна 3.
Мы решили найти более удобный, универсальный способ нахождения последней цифры степени.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
 | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 | 0 |
 | 1 | 6 | 1 | 6 | 5 | 6 | 1 | 6 | 1 | 0 |
 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Мы заполнили пятую строку, затем шестую и удивились. Оказывается, пятая степень числа оканчивается той же цифрой, что и первая степень числа; а шестая степень числа оканчивается той же цифрой, что и вторая степень этого числа; седьмая степень – что и третья степень этого числа.
К нашему удивлению, результаты в таблице повторяются через каждые четыре строки.
Мы поставили перед собой такую задачу, а нельзя ли найти способ определения последней цифры степени по остатку от деления ее показателя на 4.
II. Составление алгоритма нахождения последней цифры степени по остатку от деления ее показателя на 4.
Вернулись к нашим же примерам.
Найти последнюю цифру степеней: , 
, 
, 
;.
| | 20: 4 = 5 (остаток 0) | 1 |
| | 8: 4 = 2 (остаток 0) | 6 |
| | 36: 4 = 9 (остаток 0) | 6 |
 | 24: 4 = 6 (остаток 0) | 1 |
| | 12: 4 = 3 (остаток 0) 5 |
Итак, мы заметили, что если остаток равен 0, то для всех нечетных оснований, кроме чисел, оканчивающихся на 5, искомая цифра равна 1, а для четных, искомая цифра равна 6.
Далее мы начали подбирать такие степени, когда при делении показателя степени на 4 получаются остатки 1, 2, 3.
Например, 
.
 | 5: 4= 1 (остаток 1) | 2 |
 | 1989:4 = 497 (остаток 1) | 3 |
Если остаток равен 1, то искомая цифра будет равна последней цифре основания степени.
 | 22: 4 = 5 (остаток 2) | 4 |
 | 18: 4 = 4 (остаток 2) | 9 |
Если остаток равен 2, то искомая цифра будет равна последней цифре в записи квадрата основания.
 | 43: 4 = 10 (остаток 3) | 3 |
 | 19: 4 = 4 (остаток 3) | 8 |
Если остаток равен 3, то искомая цифра будет равна последней цифре в записи куба основания.
А если степени с очень большими показателями?
Например, 
Мы легко справились и с этой задачей.
Итак, мы получили алгоритм нахождения последней цифры степени натурального числа.
Чтобы найти последнюю цифру степени натурального числа с натуральным показателем, надо:
Найти остаток от деления показателя степени на 4;
Если остаток равен
а) 1, то искомая цифра будет совпадать с последней цифрой основания степени;
б) 2, то искомая цифра будет равна последней цифре в записи квадрата основания;
в) 3, то искомая цифра будет равна последней цифре в записи куба основания;
г) 0, то для всех нечетных оснований, кроме чисел, оканчивающихся на 5, искомая цифра равна 1, а для четных, кроме круглых чисел, искомая цифра равна 6.
Мы научились быстро находить последнюю цифру степени и попробовали расширить круг знаний. Например, мы составили такие задачи.
III. Составление упражнений на применение алгоритма.
1. Доказать, что число 
кратно 2.
2. Доказать, что 
-1 кратно 5 (при натуральном n).
3. Верно ли, что 1,6*( -1 ) – целое число при любом (натуральном) n.
4. Какой цифрой оканчивается произведение всех двузначных чисел, каждое из которых оканчивается на 7?
Как определить последнюю цифру числа в степени
Разделы: Математика
Основная часть
I. Нахождение последней цифры в записи степени натурального числа.
После изучения темы “Степень с натуральным показателем” была предложена такая задача: найти последнюю цифру степеней:
а)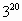 
, 
, 
, 
, 
;
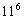
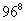
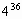
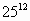
б)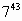 
, 
.
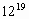
Мы заметили, что в первом случае показатели степеней составные числа, а во втором случае показатели степеней простые числа. В обоих случаях есть основания четные и нечетные. Мы сначала попробовали представить степени в виде произведения степеней с тем же основанием и одинаковыми показателями, затем воспользовались со свойствами степеней с натуральными показателями
Например, =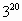 
*
*
* 
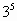
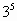
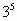
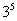
или 
В ходе решения таких задач мы поняли, что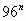
всегда оканчивается (при натуральном) n на 6.
Но вторая задача достаточно сложная, так как показатели степеней простые числа и мы не можем представить эти степени в виде произведения степеней с одинаковыми показателями, как делали раньше. Но мы нашли способы решения.
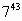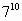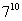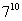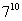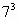 =  *  * * *  | или  | ||||||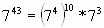
| 9 | 9 | 9 | 9 | 3 | 1 | 3 | |
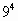 | 3 | ||||||
| 1 | 3 | 3 | |||||
| 3 | |||||||
Значит, последняя цифра степени равна 3.
Мы решили найти более удобный, универсальный способ нахождения последней цифры степени.
Решили заполнить таблицу, где в первой строке написаны цифры, которыми оканчиваются записи натуральных чисел. Во — второй строке — цифры, которыми оканчиваются соответствующие квадраты, в третьей – кубы и т.д.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
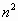 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
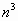 | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 | 0 |
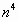 | 1 | 6 | 1 | 6 | 5 | 6 | 1 | 6 | 1 | 0 |
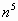 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
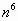 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Мы заполнили пятую строку, затем шестую и удивились. Оказывается, пятая степень числа оканчивается той же цифрой, что и первая степень числа; а шестая степень числа оканчивается той же цифрой, что и вторая степень этого числа; седьмая степень – что и третья степень этого числа.
К нашему удивлению, результаты в таблице повторяются через каждые четыре строки.
После решения этих примеров и заполнения таблицы мы пришли к выводу, что:
Мы поставили перед собой такую задачу, а нельзя ли найти способ определения последней цифры степени по остатку от деления ее показателя на 4.
II. Составление алгоритма нахождения последней цифры степени по остатку от деления ее показателя на 4.
Вернулись к нашим же примерам.
Найти последнюю цифру степеней: ,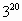 
, 
, 
;.
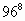
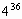
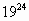
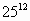
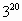| 20: 4 = 5 (остаток 0) | 1 |
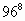| 8: 4 = 2 (остаток 0) | 6 |
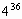| 36: 4 = 9 (остаток 0) | 6 |
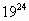 | 24: 4 = 6 (остаток 0) | 1 |
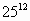| 12: 4 = 3 (остаток 0) 5 |
Итак, мы заметили, что если остаток равен 0, то для всех нечетных оснований, кроме чисел, оканчивающихся на 5, искомая цифра равна 1, а для четных, искомая цифра равна 6.
Далее мы начали подбирать такие степени, когда при делении показателя степени на 4 получаются остатки 1, 2, 3.
Например,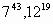 
.
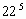 | 5: 4= 1 (остаток 1) | 2 |
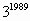 | 1989:4 = 497 (остаток 1) | 3 |
Если остаток равен 1, то искомая цифра будет равна последней цифре основания степени.
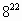 | 22: 4 = 5 (остаток 2) | 4 |
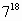 | 18: 4 = 4 (остаток 2) | 9 |
Если остаток равен 2, то искомая цифра будет равна последней цифре в записи квадрата основания.
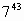 | 43: 4 = 10 (остаток 3) | 3 |
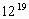 | 19: 4 = 4 (остаток 3) | 8 |
Если остаток равен 3, то искомая цифра будет равна последней цифре в записи куба основания.
А если степени с очень большими показателями?
Например, 
Мы легко справились и с этой задачей.
Итак, мы получили алгоритм нахождения последней цифры степени натурального числа.
Чтобы найти последнюю цифру степени натурального числа с натуральным показателем, надо:
Найти остаток от деления показателя степени на 4;
Если остаток равен
а) 1, то искомая цифра будет совпадать с последней цифрой основания степени;
б) 2, то искомая цифра будет равна последней цифре в записи квадрата основания;
в) 3, то искомая цифра будет равна последней цифре в записи куба основания;
г) 0, то для всех нечетных оснований, кроме чисел, оканчивающихся на 5, искомая цифра равна 1, а для четных, кроме круглых чисел, искомая цифра равна 6.
Мы научились быстро находить последнюю цифру степени и попробовали расширить круг знаний. Например, мы составили такие задачи.
III. Составление упражнений на применение алгоритма.
1. Доказать, что число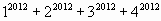 
кратно 2.
2. Доказать, что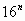 
-1 кратно 5 (при натуральном n).
3. Верно ли, что 1,6*( 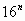-1 ) – целое число при любом (натуральном) n.
4. Какой цифрой оканчивается произведение всех двузначных чисел, каждое из которых оканчивается на 7?
Введение
«Математику уже затем учить следует,
что она ум в порядок приводит»
В ходе решения этой задачи возникла идея исследовать, а какой будет последняя цифра любого натурального числа в любой степени, есть ли какая-нибудь закономерность в том, как меняется последняя цифра степени натурального числа?
Составить опорную таблицу «Последние цифры степени», найти закономерности в них, научится вычислять последние цифры степеней.
Актуальность темы исследования обусловлена насущной необходимостью поиска быстрых алгоритмов решения практически важных задач, отработки навыков устного счета.
2. Последняя цифра степени
Для наглядности составим таблицу, где будут записаны цифры, которыми оканчиваются записи натуральных чисел:
Заполняя столбики получаем такой результат: пятая и девятая и т. д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.
3. Закономерности возведения в степень
Результаты в таблице повторяются через каждые четыре столбца.
Про числа 1 и 10 писать не будем, т.к. результат всегда будет 1 или 0 соответственно.
Любая степень чисел 5 и 6 оканчивается соответственно на 5 и на 6.
Последние цифры степеней чисел 4 и 9 повторяются через каждые два шага, при возведении в четную степень последняя цифра не меняется, будет соответственно 4 или 9, при возведении в нечетную степень изменится на 6 или 1 соответственно.
Квадрат любого натурального числа может оканчиваться на 0, 1,4, 5, 6 и 9,
Куб натурального числа может оканчиваться любой цифрой
Используя полученные результаты попробуем найти последние цифры степени по остатку от деления её показателя на 4
Если остаток равен 0 и основание нечетное, то число будет оканчиваться на 1(кроме чисел оканчивающихся на цифру 5), если основание четное (кроме круглых чисел), то числа будут оканчиваться на цифру 6.
Теперь будем подбирать такие числа, что при делении показателя степени на 4 будут давать остатки 1, 2, 3
Если остаток равен 1, то последняя цифра степени будет равна последней цифре в записи основания степени;
Если остаток равен 2, то последняя цифра степени будет равна последней цифре в записи квадрата основания;
Если остаток равен 3, то последняя цифра степени будет равна последней цифре в записи куба основания.
Значит чтобы найти последнюю цифру степени натурального числа с натуральным показателем, нужно найти остаток от деления показателя степени на 4.
4. Последние две цифры степени
Глядя на таблицу, замечаем что последние две цифры тоже повторяются, только период повторения увеличивается, кроме того у некоторых чисел 1-е не входит в период, так например:
Но начиная с 21 степени по 40 последние две цифры будут повторяться.
Последние цифры чисел 3,13 и 8 тоже будут повторятся с периодом 20, но последние две цифры чисел 3 и 13 совпадать не будут, не будут совпадать последние две цифры для степеней чисел 4 и 14 и т.д.
Последние цифры чисел 4 и 9 будут повторяться с периодом 10,последние цифры числа 6 будут повторятся с периодом 5, но число 6 не входит в период, последние цифры числа 7 будут повторятся с периодом – 4. Любая степень числа 5 (начиная со 2 –ой) и 25 будет оканчиваться на 25, а число 15 в четной степени будет оканчиваться на 25, а в нечетной на 75. Период чисел 11, тоже будет равен 10, но здесь есть еще одна закономерность:
Для числа 11 в степени – число десятков будет равно показателю степени
5. Заключение
Мы провели большую работу: составили таблицы для последней и двух последних цифр степеней и получили интересные с нашей точки зрения выводы. Результаты работы могут быть использованы на занятиях математического кружка и факультативах в 5- 7 классах для развития интереса к математике у учащихся, а так же для индивидуальной работы с теми учениками, кто интересуется математикой. Кроме того, данными выводами можно воспользоваться при подготовке к различным олимпиадам и конкурсам. Кроме того сам процесс проведённого исследования позволил нам ещё раз убедиться в своих возможностях.
6. Задачи
Определите последнюю цифру в записи числа (ответ 8)
Найдите последнюю цифру числа 2017 в степени 4207.(ответ 3)
(8+3=11, последняя цифра 1)
Найдите последнюю цифру суммы степеней числа 2 с показателями, равными 32, 69, 469, 1995, 19951995.
(6+2+2+8+8=26 последняя цифра 6)
В книге рекордов Гиннеса написано, что наибольшее известное простое число равно (− 1). Не опечатка ли это?
(опечатка. Число 23021 337 оканчивается единицей Поэтому последняя цифра числа (23021 337 − 1) равна 0, а значит, это число делится на 10 и потому составное.)
(Число 4730 оканчивается цифрой 9, а число 3950 — цифрой 1 Значит, их сумма оканчивается на 0 и потому делится на 10.)
Последние две цифры числа 7 7 образуют число 43 (это можно вычислить непосредственно, отбрасывая при каждом умножении все цифры результата, кроме последних двух). Значит, число 7 7 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени). В нашем случае 43 делится на 4 с остатком 3, значит, и 7 7 делится на 4 с остатком 3 (согласно признаку делимости на 4). А у всех степеней семёрки, показатели которых делятся на 4 с остатком 3, последняя цифра равна 3).
Сейчас на часах 10:00. Какое время они будут показывать через 102938475 часов?
(У часов период повторения равен 24, значит число 102938475 разделить на 24 = 4289103,12… 102938475 — (4289103 * 24) = 3. Значит время которое часы будут показывать через 102938475 часов равно 10+3 = 13 часов, через 102938475 часы будут показывать 13:00).
11. Доказать, что число кратно 2.
7. Использованная литература
1. «Все задачи «Кенгуру» 1994-2008- Санкт-Петербург, 2008.
2. «Задачи для подготовки к олимпиадам. Математика 5-8 классы» сост. Н.В. Заболотнева. – Волгоград: Учитель, 2007.- 99с.
3. Лихтарников Л.М. Занимательные логические задачи. (Для учащихся начальной школы) Оформление С. Григорьева — СПб.: Лань, МИК, 1996.- 125с.
4. Л.М.Лоповок 1000 проблемных задач по математике. Книга для учащихся Москва : Просвещение, 1995
5. Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы — М.: Просвещение, 1990.- 224 с.: ил.
6. Чулков П.В. Математика. Школьные олимпиады: методическое пособие. 5- кл./ П.В. Чулков.- М.: Издательство НЦ ЭНАС, 2007.- 88с. (Портфель учителя).
7. Шуба М.Ю. Занимательные задачи в обучении математике: Книга для учителя. — 2-е изд.-М.: Просвещение, 1995.- 22с.
МОУ «Шербакульская средняя общеобразовательная школа №1»
Научное сообщество учащихся «Поиск»
Тема: « Последняя цифра степени.»
Выполнила: ученица 7 «б» класса
Руководитель: Пушило Т.Л.
· Последняя цифра степени.
· Закономерности возведения в степень
· Две последних цифры степени.
Однажды, листая страницы книги «Тысяча проблемных задач по математике», я увидела с первого взгляда очень трудную задачу, точнее сказать пример надо было найти последнюю цифру суммы
Потом я подумала, а ведь должен же быть, какой-нибудь рациональный способ вычисления и тут я принялась считать…
Гипотеза: Можно ли сказать какой будет последняя цифра у любой степени?
· Узнать, можно ли построить таблицу последних цифр различных степеней.
· Найти закономерность в них.
· Используя таблицу практиковаться на более легких задачах и решить вышеупомянутый пример и если получится более сложные.
Последняя цифра степени.
| 2 1 = 2 2 5 = 32 2 9 = 512 | 2 2 = 4 2 6 = 64 2 10 = 1024 | 2 3 = 8 2 7 = 128 2 11 = 2048 | 2 4 = 16 2 8 = 256 2 12 = 4096 |
Теперь попробуем пользоваться таблицей, но в таблице 4 числа, а показатель степени 22, однако, после последнего числа этот «круг» начинается заново. Поэтому, показатель степени 22 делим на 4, получаем число 5 и остаток 2 т.е мы сделаем 5 «кругов», и отсчитаем ещё 2 в перед, а второе число – это 4, значит, таблица работает.
А теперь посмотрим, можно ли составить таблицы для остальных чисел. Все описывать не буду, лишь скажу, что у меня получилось составить таблицу для всех чисел от 1 до 10, а далее будет повторяться, допустим, у 12 последние числа будут такие же, как и у 2, а у 25 – так же, как и у 5.
Закономерности возведения в степень:
Две последних цифры степени.