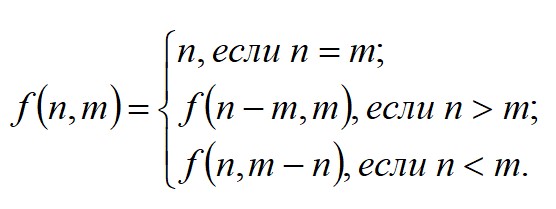BestProg
Рекурсия. Примеры решения задач. Преимущества и недостатки рекурсии
Содержание
Поиск на других ресурсах:
1. Что такое рекурсия? Что называется рекурсией?
Любая функция (метод) в своем теле может вызывать сама себя. Рекурсия – это такой способ определения функции, при котором результат возврата из функции для данного значения аргумента определяется на основе результата возврата из той же функции для предыдущего (меньшего или большего) значения аргумента.
Если функция (метод) вызывает сам себя, то такой вызов называется рекурсивным вызовом функции. При каждом рекурсивном вызове запоминаются предыдущие значения внутренних локальных переменных и полученных параметров функции. Чтобы следующий шаг рекурсивного вызова отличался от предыдущего, значение как-минимум одного из параметров функции должно быть изменено. Остановка процесса рекурсивных вызовов функции происходит, когда изменяемый параметр достиг некоторого конечного значения, например, обработан последний элемент в массиве.
2. Объяснения к реализации задач на рекурсию. Как правильно организовать рекурсивный вызов функции?
Рекурсивное обращение к функции может быть осуществлено, если алгоритм определен рекурсивно.
Чтобы циклический процесс преобразовать в рекурсивный, нужно уметь определить (выделить) три важных момента:
3. Поиск суммы элементов массива. Пример
По подобному примеру можно создавать собственные рекурсивные функции, которые определяют любые суммы элементов любых массивов.
где n – количество элементов массива. Программный код функции следующий:
Как видно из примера, в рекурсивную функцию Sum() передается 3 параметра:
Выход из функции осуществляется, если будет обработан последний элемент массива. Условие прекращения рекурсивного процесса имеет вид:
Для суммирования текущего значения A[i] со следующими указывается строка:
Использование функции Sum() в другом программном коде может быть, например, таким:
4. Пример подсчета количества вхождений заданного символа в строке
Реализация функции Count() следующая:
5. Пример нахождения факториала числа – n!
Вычисление факториала числа методом рекурсии есть почти в каждом учебнике. Факториал числа вычисляется по формуле
Рекурсивный вызов можно организовать двумя способами:
В данном примере разработаны две функции, которые находят факториал обоими способами. Программный код функций следующий:
Использование функций в другом программном коде может быть следующим:
6. Программа нахождения наибольшего общего делителя (алгоритм Евклида). Пример
В примере определяется наибольший общий делитель по формуле Евклида:
Программный код функции следующий:
Использование функции MaxDiv() может быть следующим:
7. Подсчет количества элементов массива, больших заданного числа. Пример
Использование метода Count() в другом методе
8. Преимущества использования рекурсии в программах. Пример
Рекурсию часто сравнивают с итерацией. Организация циклического процесса с помощью рекурсии имеет свои преимущества и недостатки.
Можно выделить следующие взаимосвязанные преимущества рекурсии:
Недостатки рекурсии состоят в следующем:
Как работает рекурсия – объяснение в блок-схемах и видео
Представляю вашему вниманию перевод статьи Beau Carnes How Recursion Works — explained with flowcharts and a video.
«Для того чтобы понять рекурсию, надо сначала понять рекурсию»
Рекурсию порой сложно понять, особенно новичкам в программировании. Если говорить просто, то рекурсия – это функция, которая сама вызывает себя. Но давайте попробую объяснить на примере.
Представьте, что вы пытаетесь открыть дверь в спальню, а она закрыта. Ваш трехлетний сынок появляется из-за угла и говорит, что единственный ключ спрятан в коробке. Вы опаздываете на работу и Вам действительно нужно попасть в комнату и взять вашу рубашку.
Вы открываете коробку только чтобы найти… еще больше коробок. Коробки внутри коробок и вы не знаете, в какой из них Ваш ключ. Вам срочно нужна рубашка, так что вам надо придумать хороший алгоритм и найти ключ.
Есть два основных подхода в создании алгоритма для решения данной проблемы: итеративный и рекурсивный. Вот блок-схемы этих подходов:
Какой подход для Вас проще?
В первом подходе используется цикл while. Т.е. пока стопка коробок полная, хватай следующую коробку и смотри внутрь нее. Ниже немного псевдокода на Javascript, который отражает то, что происходит (Псевдокод написан как код, но больше похожий на человеческий язык).
В другом подходе используется рекурсия. Помните, рекурсия – это когда функция вызывает саму себя. Вот второй вариант в псевдокоде:
Оба подхода выполняют одно и тоже. Основный смысл в использовании рекурсивного подхода в том, что однажды поняв, вы сможете легко его читать. В действительности нет никакого выигрыша в производительности от использования рекурсии. Порой итеративный подход с циклами будет работать быстрее, но простота рекурсии иногда предпочтительнее.
Поскольку рекурсия используется во многих алгоритмах, очень важно понять как она работает. Если рекурсия до сих пор не кажется Вам простой, не беспокойтесь: Я собираюсь пройтись еще по нескольким примерам.
Граничный и рекурсивный случай
То, что Вам необходимо принять во внимание при написании рекурсивной функции – это бесконечный цикл, т.е. когда функция вызывает саму себя… и никогда не может остановиться.
Допустим, Вы хотите написать функцию подсчета. Вы можете написать ее рекурсивно на Javascript, к примеру:

Эта функция будет считать до бесконечности. Так что, если Вы вдруг запустили код с бесконечным циклом, остановите его сочетанием клавиш «Ctrl-C». (Или, работая к примеру в CodePen, это можно сделать, добавив “?turn_off_js=true” в конце URL.)
Рекурсивная функция всегда должна знать, когда ей нужно остановиться. В рекурсивной функции всегда есть два случая: рекурсивный и граничный случаи. Рекурсивный случай – когда функция вызывает саму себя, а граничный – когда функция перестает себя вызывать. Наличие граничного случая и предотвращает зацикливание.
И снова функция подсчета, только уже с граничным случаем:

То, что происходит в этой функции может и не быть абсолютно очевидным. Я поясню, что произойдет, когда вы вызовете функцию и передадите в нее цифру 5.
Сначала мы выведем цифру 5, используя команду Console.Log. Т.к. 5 не меньше или равно 1, то мы перейдем в блок else. Здесь мы снова вызовем функцию и передадим в нее цифру 4 (т.к. 5 – 1 = 4).
Мы выведем цифру 4. И снова i не меньше или равно 1, так что мы переходим в блок else и передаем цифру 3. Это продолжается, пока i не станет равным 1. И когда это случится мы выведем в консоль 1 и i станет меньше или равно 1. Наконец мы зайдем в блок с ключевым словом return и выйдем из функции.
Стек вызовов
Рекурсивные функции используют так называемый «Стек вызовов». Когда программа вызывает функцию, функция отправляется на верх стека вызовов. Это похоже на стопку книг, вы добавляете одну вещь за одни раз. Затем, когда вы готовы снять что-то обратно, вы всегда снимаете верхний элемент.
Я продемонстрирую Вам стек вызовов в действии, используя функцию подсчета факториала. Factorial(5) пишется как 5! и рассчитывается как 5! = 5*4*3*2*1. Вот рекурсивная функция для подсчета факториала числа:
Теперь, давайте посмотрим что же происходит, когда вы вызываете fact(3). Ниже приведена иллюстрация в которой шаг за шагом показано, что происходит в стеке. Самая верхняя коробка в стеке говорит Вам, что вызывать функции fact, на которой вы остановились в данный момент:

Заметили, как каждое обращение к функции fact содержит свою собственную копию x. Это очень важное условие для работы рекурсии. Вы не можете получить доступ к другой копии функции от x.
Нашли уже ключ?
Давайте кратенько вернемся к первоначальному примеру поиска ключа в коробках. Помните, что первым был итеративный подход с использованием циклов? Согласно этому подходу Вы создаете стопку коробок для поиска, поэтому всегда знаете в каких коробках вы еще не искали.

Но в рекурсивном подходе нет стопки. Так как тогда алгоритм понимает в какой коробке следует искать? Ответ: «Стопка коробок» сохраняется в стеке. Формируется стек из наполовину выполненных обращений к функции, каждое из которых содержит свой наполовину выполненный список из коробок для просмотра. Стек следит за стопкой коробок для Вас!
И так, спасибо рекурсии, Вы наконец смогли найти свой ключ и взять рубашку!

Вы также можете посмотреть мое пятиминутное видео про рекурсию. Оно должно усилить понимание, приведенных здесь концепций.
Заключение от автора
Надеюсь, что статья внесла немного больше ясности в Ваше понимание рекурсии в программировании. Основой для статьи послужил урок в моем новом видео курсе от Manning Publications под названием «Algorithms in Motion». И курс и статься написаны по замечательной книге «Grokking Algorithms», автором которой является Adit Bhargava, кем и были нарисованы все эти замечательные иллюстрации.
И наконец, чтобы действительно закрепить свои знания о рекурсии, Вы должны прочитать эту статью, как минимум, еще раз.
От себя хочу добавить, что с интересом наблюдаю за статьями и видеоуроками Beau Carnes, и надеюсь что Вам тоже понравилась статья и в особенности эти действительно замечательные иллюстрации из книги A. Bhargav «Grokking Algorithms».
BestProg
Рекурсия. Примеры рекурсивных методов (функций) в C#
В данной теме показано, что с помощью рекурсии можно легко разрабатывать методы, которые решают задачи любой сложности.
Содержание
Поиск на других ресурсах:
1. Что такое рекурсия? Что такое рекурсивный метод (функция)?
Рекурсия – это разработка метода таким образом, чтобы он вызывал сам себя. Рекурсивные вызовы метода должны завершаться при достижении некоторого условия. В противном случае произойдет переполнение памяти и программа «зависнет» не достигнув вычисления необходимого результата.
Рекурсивный метод – это метод, который вызывает сам себя. В рекурсивном методе помещается вызов этого же метода по его имени.
Последовательный процесс рекурсивных вызовов метода подобен циклическому процессу.
⇑
2. Как работает рекурсивный вызов метода?
Если метод вызывает сам себя, то в памяти происходят следующие процессы:
⇑
3. Какие преимущества дает использование рекурсии в программах?
Рекурсию всегда сравнивают с итерацией. Для многих задач рекурсия дает следующие взаимосвязанные преимущества:
⇑
4. Какие недостатки использования рекурсии в программах?
В сравнении с итерационными вызовами, построение рекурсивных вызовов имеет следующие недостатки:
⇑
5. Пример вычисления суммы ряда
Разработать рекурсивную функцию вычисления суммы ряда
S = 5 + 10 + 15 + … + 5·n,
Программный код функции следующий
⇑
6. Пример конвертирования строки «AAABCCCCAADDDEF» => «3AB4C2A3DEF»
Данная задача очень удобно решается с помощью рекурсии. По данному образцу можно разрабатывать рекурсивные функции, которые обрабатывают строки по любым правилам.
В рекурсивной функции ConvertStr() рекурсивно просматривается вся строка. На каждом рекурсивном вызове обрабатывается один символ строки. В зависимости от позиции текущего обрабатываемого символа происходит соответствующий рекурсивный вызов функции.
Рекурсивная функция содержит следующие параметры:
Использование функции в другом программном коде
⇑
7. Пример сравнения строк
Разработать рекурсивную функцию, которая сравнивает две строки на идентичность. Две строки считаются идентичными, если:
Рекурсивная функция должна получать следующие параметры:
Использование функции в другом программном коде
⇑
8. Пример рекурсивной функции реверсирования строки
Программный код функции следующий
В функции RString() определение последнего символа в строке происходит по формуле:
Поскольку функция должна что-то возвратить, то перед формулой обработки строки нужно вставить оператор return
Использование функции RString() в другом методе может быть следующим:
⇑
9. Пример рекурсивной функции определения, является ли строка симметричной
В вышеприведенной функции сравниваются символы, которые размещаются на позициях i+pos и j-pos строки с помощью оператора if
есть середина диапазона (j-i) в соответствии с условием задачи.
Использование функции в другом программном коде
Рекурсивная функция C++
Известно, что процесс, в котором конкретная функция вызывает себя прямо или косвенно, является рекурсией, а соответствующая функция является рекурсивной функцией. Процесс рекурсии имеет дело с итерацией нескольких чисел для одной и той же функции. Чтобы завершить выполнение процесса рекурсии, нам нужно иметь базовый случай, за которым следует любое условие. В этом руководстве используются функции рекурсии в C ++, поэтому перед чтением вы должны быть знакомы с основами этого языка программирования.
Рекурсия — это эффективный подход к решению таких проблем, как сложные математические вычислительные задачи. Это делается путем разделения задачи на подзадачи. Этот процесс осуществляется в соответствии с правилом «разделяй и властвуй». Необязательно всегда использовать процесс рекурсии в вашей программе для повторения. Любая проблема, решаемая с помощью рекурсии, также может быть решена с помощью итераций. Но рекурсивная функция более эффективна в программировании, поскольку код очень короткий и легко понятный при выполнении той же задачи. Процесс рекурсии всегда рекомендуется для таких задач, как поиск и сортировка, обход дерева и т.д.
Примечание: процесс рекурсии должен иметь условие завершения или базовый класс. Во втором случае это приведет к бесконечному количеству выполнений, как цикл итераций.
Синтаксис рекурсивной функции (C ++)
Базовый синтаксис рекурсивной функции имеет следующий вид:
Идея состоит в том, чтобы разделить проблему на множество более мелких проблем, а затем добавить все базовые условия, которые могут остановить рекурсию.
Базовое состояние
В любой рекурсивной программе решение более крупной проблемы выражается в более мелких задачах.
int fact ( int n )
<
if ( n = 1 ) // base case
return 1 ;
else
‘other statement’
>
Утверждение / условие «n ( val 1 )
В то время как основная функция применяется к «else» части функции. Это рекурсивная функция.
Значение отображается до и после этого оператора, поэтому выходные данные будут содержать числа в порядке убывания и возрастания. Выполнение кода выполняется компилятором g ++. ’-o’ используется для сохранения вывода исходного кода в выходной файл.
Теперь мы хотим увидеть эффект базового условия в этой программе. Мы увидим результирующее значение; если мы удалим из той же программы оператор if-else, как описано выше, каким будет результат.
Вы можете видеть, что остальной код не изменился после удаления условного оператора. После удаления базового оператора результат будет выглядеть, как на изображении ниже. Для этого выполнения не будет определенной конечной точки. Вы можете заметить, что на выходе получается бесконечное число.
Этот же вывод занимает много строк, пока не появится сообщение о дампе ядра.
Работа рекурсии
Предположим, что программист хочет определить сумму первых n чисел, существует много способов определить сумму, но самый простой — сложить числа, начиная с 1 до n. Итак, функция будет выглядеть так:
Приведенный выше пример представляет собой простое сложение чисел. Второй подход связан с использованием рекурсивной функции.
F ( n ) = 1 n = 1
F ( n ) = n + f ( n — 1 ) n > 1
Теперь вы можете указать на разницу между обоими подходами. Во втором подходе f () — это основное несходство, как оно само называется.
Рекурсия бывает двух типов. Один из них — прямая рекурсия. Второй — косвенная рекурсия. Функция называется косвенной рекурсивной, если у нее есть вызов другой функции и эта другая функция прямо или косвенно вызывает первую функцию. Пример прямой рекурсии проиллюстрирован как:
В то время как образец для косвенной рекурсии представлен как:
void f ( int n ) <
f1 ( ) ; >
void f1 ( int n ) <
f ( ) ;
return ; >
Теперь мы подробно рассмотрим оба типа рекурсивных функций на некоторых основных примерах.
Прямая рекурсия
Пример 1
В этом примере рассматривается расчет ряда Фибоначчи. Опять же, концепция та же; здесь используется условный оператор, чтобы остановить условие; значение должно быть равно нулю. В противном случае, если значение равно 1 или 2, оно вернет 1. Поскольку для формирования этого ряда требуется 2 числа, поэтому число, используемое в основной программе, должно быть больше 2. Формула оператора для Фибоначчи записывается в ’ остальное искусство условия. В основном это рекурсия программы.
В то время как основная функция инициирует функциональный вызов в обход значения. Это значение — число, до которого должен быть вывод. Вывод можно проверить через терминал Linux с помощью компилятора g ++.
Пример 2
В этом примере рассматривается факториальное вычисление числа. Для этого расчета число должно быть больше 1, поэтому здесь мы применили базовое условие; если эта часть оператора if выполняется, то программа завершается; в противном случае к числу применяется математическая операция.
Это функция рекурсии, в которой ответ функции снова используется в вызове функции.
Полученное значение показано ниже.
Косвенная рекурсия
Мы применим тот же расчет факториала косвенно. Как мы описали ранее, при косвенной рекурсии функции не вызывают ее, поэтому для этой цели нам нужна другая функция. Возьмем пример, который выполняет две функции. В функции A функция рекурсии объявлена так же, как в предыдущем примере, но вызов функции предназначен для второй функции, Function-B. Функция B содержит тот же метод расчета и рекурсивный вызов функции A.
В основной программе выполняется вызов функции A.
Когда вы увидите результат, вы заметите, что ответ для обоих методов рекурсии одинаковый, но разница только в используемом подходе.
Заключение
«Рекурсивная функция C ++» имеет много преимуществ, поскольку она используется в процессах поиска и сортировки. Базовое условие играет основную роль в выполнении рекурсии, поскольку оно ограничивает вывод и бесконечное выполнение. Здесь объясняются часто используемые примеры, чтобы дать пользователю понимание рекурсии.
Урок №107. Рекурсия и Числа Фибоначчи
Обновл. 28 Авг 2021 |
На этом уроке мы рассмотрим, что такое рекурсия в языке C++ и зачем её использовать, а также последовательность Фибоначчи и факториал целого числа.
Рекурсия
Рекурсивная функция (или просто «рекурсия») в языке C++ — это функция, которая вызывает сама себя. Например:
На уроке о стеке и куче в С++ мы узнали, что при каждом вызове функции, определенные данные помещаются в стек вызовов. Поскольку функция countOut() никогда ничего не возвращает (она просто снова вызывает countOut()), то данные этой функции никогда не вытягиваются из стека! Следовательно, в какой-то момент, память стека закончится и произойдет переполнение стека.
Условие завершения рекурсии
Рекурсивные вызовы функций работают точно так же, как и обычные вызовы функций. Однако, программа, приведенная выше, иллюстрирует наиболее важное отличие простых функций от рекурсивных: вы должны указать условие завершения рекурсии, в противном случае — функция будет выполняться «бесконечно» (фактически до тех пор, пока не закончится память в стеке вызовов).
Условие завершения рекурсии — это условие, которое, при его выполнении, остановит вызов рекурсивной функции самой себя. В этом условии обычно используется оператор if.
Вот пример функции, приведенной выше, но уже с условием завершения рекурсии (и еще с одним дополнительным выводом текста):
Когда мы запустим эту программу, то countOut() начнет выводить:
push 4
push 3
push 2
push 1
Если сейчас посмотреть на стек вызовов, то увидим следующее:
countOut(1)
countOut(2)
countOut(3)
countOut(4)
main()
Таким образом, результат выполнения программы, приведенной выше:
push 4
push 3
push 2
push 1
pop 1
pop 2
pop 3
pop 4
Стоит отметить, что push выводится в порядке убывания, а pop — в порядке возрастания. Дело в том, что push выводится до вызова рекурсивной функции, а pop выполняется (выводится) после вызова рекурсивной функции, когда все экземпляры countOut() вытягиваются из стека (это происходит в порядке, обратном тому, в котором эти экземпляры были введены в стек).
Теперь, когда мы обсудили основной механизм вызова рекурсивных функций, давайте взглянем на несколько другой тип рекурсии, который более распространен:
Рассмотреть рекурсию с первого взгляда на код не так уж и легко. Лучшим вариантом будет посмотреть, что произойдет при вызове рекурсивной функции с определенным значением. Например, посмотрим, что произойдет при вызове вышеприведенной функции с value = 4 :
sumCount(4). 4 > 1, поэтому возвращается sumCount(3) + 4
sumCount(3). 3 > 1, поэтому возвращается sumCount(2) + 3
sumCount(2). 2 > 1, поэтому возвращается sumCount(1) + 2
sumCount(1). 1 = 1, поэтому возвращается 1. Это условие завершения рекурсии
Теперь посмотрим на стек вызовов:
sumCount(1) возвращает 1
sumCount(2) возвращает sumCount(1) + 2, т.е. 1 + 2 = 3
sumCount(3) возвращает sumCount(2) + 3, т.е. 3 + 3 = 6
sumCount(4) возвращает sumCount(3) + 4, т.е. 6 + 4 = 10
На этом этапе уже легче увидеть, что мы просто добавляем числа между 1 и значением, которое предоставил caller. На практике рекомендуется указывать комментарии возле рекурсивных функций, дабы облегчить жизнь не только себе, но, возможно, и другим людям, которые будут смотреть ваш код.
Рекурсивные алгоритмы
Числа Фибоначчи
Одним из наиболее известных математических рекурсивных алгоритмов является последовательность Фибоначчи. Последовательность Фибоначчи можно увидеть даже в природе: ветвление деревьев, спираль ракушек, плоды ананаса, разворачивающийся папоротник и т.д.
Спираль Фибоначчи выглядит следующим образом:
Каждое из чисел Фибоначчи — это длина горизонтальной стороны квадрата, в которой находится данное число. Математически числа Фибоначчи определяются следующим образом:
F(n) = 0, если n = 0
1, если n = 1
f(n-1) + f(n-2), если n > 1
Следовательно, довольно просто написать рекурсивную функцию для вычисления n-го числа Фибоначчи: