Слово Как написать уравнение перпендикуляра к плоскости - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

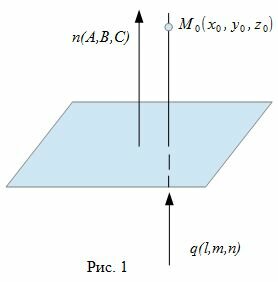
Общее уравнение плоскости имеет вид:

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

Общее уравнение плоскости имеет вид (1), где :

Источник

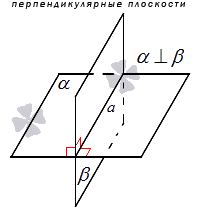
Перпендикулярные плоскости, условие перпендикулярности плоскостей

Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.

Перпендикулярные плоскости – основные сведения

При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.

При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.

Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.

Перпендикулярность плоскостей – признак и условие перпендикулярности

На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.

Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.

Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.

Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.

Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.

Рассмотрим подробнее на примерах.

Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.

Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.

Ответ: плоскости не перпендикулярны.

Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.

Ответ: плоскости перпендикулярны.

Источник

Уравнения прямой, которая проходит через заданную точку и перпендикулярна к заданной плоскости.

В этой статье мы разберемся с нахождением уравнений прямой, которая в прямоугольной системе координат в трехмерном пространстве проходит через заданную точку и перпендикулярна к заданной плоскости. Сначала разберем принцип составления уравнений такой прямой, после чего перейдем к решению задач.

Навигация по странице.

Принцип составления уравнений прямой, проходящей через заданную точку перпендикулярно к заданной плоскости.

Прежде чем приступить к составлению уравнений прямой, которая проходит через заданную точку пространства перпендикулярно к заданной плоскости, освежим в памяти один момент.

В 10 классе на уроках геометрии доказывается теорема: через любую точку трехмерного пространства проходит единственная прямая, перпендикулярная к заданной плоскости. Таким образом, мы можем определить конкретную прямую, указав точку, через которую она проходит, и плоскость, к которой она перпендикулярна.

Сформулируем условие задачи.

Итак, задача нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости, решена. Осталось лишь рассмотреть несколько решенных примеров.

Примеры нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости.

В этом пункте статьи мы приведем подробные решения наиболее характерных задач, в которых находятся уравнения прямой, проходящей через заданную точку пространства перпендикулярно к заданной плоскости.

Начнем с самого простого случая, когда требуется написать уравнения прямой, проходящей через заданную точку перпендикулярно к одной из координатных плоскостей.

.

Аналогично решается задача, в условии которой даны координаты точки, через которую проходит прямая, и задана плоскость с помощью общего уравнения плоскости.

.

В заключении рассмотрим пример составления уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к плоскости, заданной тремя не лежащими на одной прямой точками.

Тогда, , а в координатной форме (при необходимости обращайтесь к статье координаты вектора).

Приведем второй способ решения этой задачи.

.

Источник

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

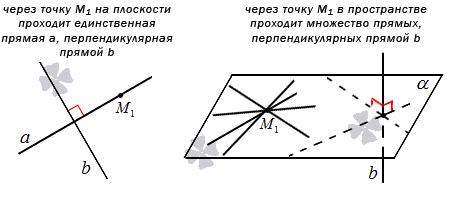
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Полученное уравнение является искомым.

Источник

Как написать уравнение перпендикуляра к плоскости

В планиметрии построение перпендикуляра основано на том, что он соединяет данную точку и точку, симметричную с ней относительно рассматриваемой прямой. Если мы хотим составить понятие о перпендикуляре к плоскости, то можно взять любую точку, лежащую вне этой плоскости, отразить эту точку в данной плоскости, как в зеркале, и соединить данную точку с ее отражением; тогда получим перпендикуляр к плоскости. Следует, однако, заметить, что в случае отражения относительно прямой все дело сводилось к сгибу плоскости вдоль данной прямой, т. е. к движению, хотя и производимому в пространстве. Отражение же в плоскости уже не сводится к движению. Поэтому изложение вопроса о перпендикуляре к плоскости сложнее соответствующего изложения вопроса о перпендикуляре к прямой в планиметрии, оно опирается на следующее известное читателю

Определение. Прямая называется перпендикуляром к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Так как угол между двумя скрещивающимися прямыми равен по определению углу между пересекающимися прямыми, параллельными данным, то прямая а (рис. 337), перпендикулярная ко всем прямым плоскости К, проходящим через точку пересечения прямой а с плоскостью К, будет перпендикулярна и к плоскости К. Действительно, она образует прямой угол с любой прямой в плоскости так как она перпендикулярна к прямой b, проведенной в этой плоскости через точку параллельно b.

В действительности имеет место гораздо более простой Признак перпендикулярности прямой и плоскости. Прямая, перпендикулярная к двум пересекающимся прямым плоскости, перпендикулярна к этой плоскости.

Доказательство. Пусть на рис. 338 прямая а перпендикулярна к двум пересекающимся прямым , лежащим в плоскости Х. В силу сделанного выше замечания мы можем, не нарушая общности, предположить, что прямая а проходит через точку пересечения прямых тип. Требуется доказать, что прямая а перпендикулярна и к любой прямой плоскости в силу того же замечания можно предположить, что прямая проходит через точку . Сделаем следующие вспомогательные построения: на прямой а возьмем произвольную точку М и точку М на продолжении по другую сторону плоскости Я на расстоянии от точки Три прямые в плоскости X пересечем какой-либо прямой с, не проходящей через точки пересечения обозначим соответственно Р, Q, R. Соединим точки М и М с точками Р, Q, R. Треугольники равны, так как они прямоугольные, катеты равны по построению, а катет общий; значит, равны и их гипотенузы: (можно еще проще заметить, что МР — МР, как наклонные с равными проекциями). Отрезки MQ, MQ также равны. Значит, равны треугольники MPQ и MPQ (по трем сторонам). Отсюда заключаем, что равны треугольники MQR и у них между равными сторонами MQ и MQ и общей стороной QR заключены равные углы: (соответственные углы в равных треугольниках). Теперь уже видно, что равны и треугольники трем сторонам). Таким образом, углы MMUR и равны, и так как они смежные, то каждый из них прямой. Утверждение доказано.

К любой прямой можно провести перпендикулярную плоскость.

В самом деле, возьмем произвольную прямую и в любой ее точке проведем к ней два каких-либо перпендикуляра (лежащие в каких-либо двух плоскостях, проведенных через эту прямую). Через них, как через две пересекающиеся прямые, проходит плоскость. По предыдущему, данная прямая служит перпендикуляром к этой плоскости.

Из проведенных рассуждений также следует вывод: все прямые, перпендикулярные к данной прямой в одной из ее точек, лежат в одной плоскости, перпендикулярной к этой прямой.

В любой точке плоскости также можно восставить перпендикуляр к ней.

Для этого достаточно провести через данную в плоскости точку две прямые, лежащие в этой плоскости, а затем построить в той же точке две плоскости, перпендикулярные к проведенным прямым. Имея общую точку, эти две плоскости пересекутся по прямой, которая будет одновременно перпендикулярна к двум пересекающимся прямым в плоскости и, следовательно, перпендикулярна к самой плоскости.

Источник