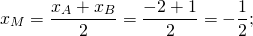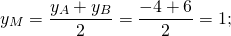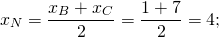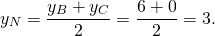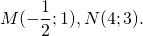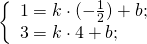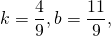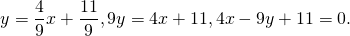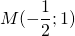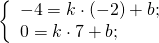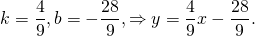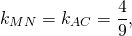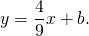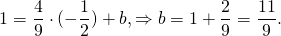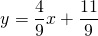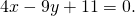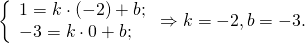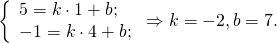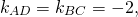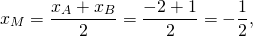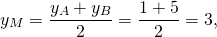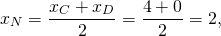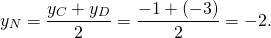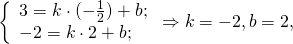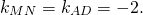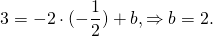Уравнение средней линии
Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?
Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.
Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.
1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.
М — середина отрезка AB, N — середина BC.
Составим уравнение прямой MN, например, в виде y=kx+b:
Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.
— середина отрезка AB. Составим уравнение прямой AC:
Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.
Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:
то есть уравнение прямой MN ищем в виде
Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:
Таким образом, уравнение прямой MN
Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.
Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).
Сначала следует определить основания данной трапеции.
Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.
Поскольку угловые коэффициенты прямых равны:
то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.
Составим уравнение прямой MN, M(-1/2;3), N(2;-2):
Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:
Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.
Написать уравнение сторон равнобедренной трапеции
Линейные образы на плоскости и в пространстве: Написать уравнение сторон равнобедренной трапеции
Написать уравнение сторон равнобедренной трапеции, зная середины ее оснований (1;1), (2;8) и точки.
в равнобедренной трапеции боковая сторона
в равнобедренной трапеции боковая сторона с=13 а основания а=21 b=11 вычислить длину диолонали.
Периметр равнобедренной трапеции по основанию и углу
Условие задачи следующее: В равнобедренной трапеции меньшая основа=боковой стороне,большая.
Катет равен боковой стороне равнобедренной трапеции
Имеется равнобокая трапеция ABMN, которая вписана в окружность. Так же известно, что на нижнем.
Далее, координаты середины М отрезка АВ равны полусумме координат его концов; отсюда М((х+4)/2,(у-3)/2). Так как М лежит на прямой L, то
7(х+4)/2-(у-3)/2-6=0. (Это второе уравнение.)
Решайте систему для вычисления координат точки В.
Добавлено через 13 минут
Чтобы не заморачиваться с точкой М на прямой, формулу можно ещё упростить:
Написать уравнение трёх сторон квадрата
1) Дана одна из сторон квадрата АВ х+3у-3=0 и дана точка М(-2;0) пересечения его диагоналей d1 и.
Найти уравнения боковых сторон трапеции
Не могу справиться с заданием! Решения подобных задач тоже не нахожу..
Найти длину боковой стороны равнобедренной трапеции с углом при основании α (альфа), который при заданной площади S имела бы наименьший периметр
Помогите пожалуйста решить задачу: Найти длину боковой стороны равнобедренной трапеции с углом при.