Как написать функцию в matlab

Морфемный разбор слова:

Однокоренные слова к слову:

Документация

Объявите имя функции, входные параметры и выходные параметры

Синтаксис

Описание

Можно сохранить функцию:

В файле функции, который содержит только функциональные определения. Имя файла должно совпадать с именем первой функции в файле.

В файле скрипта, который содержит команды и функциональные определения. Функции должны быть в конце файла. Файлы скрипта не могут иметь того же имени как функция в файле. Функции поддерживаются в скриптах в R2016b или позже.

Файлы могут включать несколько локальных функций или вложенных функций. Для удобочитаемости используйте end ключевое слово, чтобы указать на конец каждой функции в файле. end ключевое слово требуется когда:

Любая функция в файле содержит вложенную функцию.

Функция является локальной функцией в файле функции, и любая локальная функция в файле использует end ключевое слово.

Функция является локальной функцией в файле скрипта.

Примеры

Функция с одним Выводом

Задайте функцию в файле с именем average.m это принимает входной вектор, вычисляет среднее значение значений и возвращает один результат.

Вызовите функцию из командной строки.

Функция с несколькими Выходными параметрами

Задайте функцию в файле с именем stat.m это возвращает среднее и стандартное отклонение входного вектора.

Вызовите функцию из командной строки.

Функция в файле скрипта

Задайте скрипт в файле с именем integrationScript.m это вычисляет значение подынтегрального выражения в и вычисляет область под кривой от 0 до . Включайте локальную функцию, которая задает подынтегральное выражение .

Примечание: Включая функции в скриптах требует MATLAB® R2016b или позже.

Несколько функций в функциональном файле

Функциональный avg local function. Локальные функции только доступны для других функций в том же файле.

Вызовите функциональный stat2 из командной строки.

Функция с валидацией аргумента

Задайте функцию, которая ограничивает вход числовым вектором, который не содержит Inf или NaN элементы. Эта функция использует arguments ключевое слово, которое допустимо для MATLAB ® версии R2019b и позже.

Вызывание функции с вектором, который содержит элемент, который является NaN нарушает объявление входного параметра. Это нарушение приводит к ошибке, будучи выданным mustBeFinite функция валидации.

Смотрите также

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация MATLAB

Поддержка

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник

Содержание

В этом пособии рассказывается о применении пакета MatLab для анализа многомерных данных. Этот текст не является учебником по MatLab. В нем приведены только базовые сведения о работе в этой среде, необходимые для реализации основных алгоритмов. Более подробное изложение можно найти здесь.

В пособии интенсивно используются понятия и методы матричной алгебры – вектор, матрица, и т.п. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, пособие «Матрицы и векторы».

Для практического воплощения хемометрических методов используются как специализированные пакеты программ (например, the Unsrambler или SIMCA), так и статистические пакеты общего назначения (например, SPSS или Statistica). Среди средств общего назначения, используемых в хемометрике, особое место занимает пакет MatLab. Его популярность необычайно высока. Это объясняется тем, что MatLab является мощным и универсальным обработки многомерных данных. Сама структура пакета делает его удобным средством для проведения матричных вычислений. Спектр проблем, исследование которых может, осуществлено при помощи MatLab, охватывает: матричный анализ, обработку сигналов и изображений, нейронные сети и многие другие. MatLab — это язык высокого уровня, имеющий открытый код, что дает возможность опытным пользователям разбираться в запрограммированных алгоритмах. Простой встроенный язык программирования позволяет легко создавать собственные алгоритмы. За много лет использования MatLab создано огромное количество функций и ToolBox (пакетов специализированных средств). Самым популярным является пакет PLS ToolBox компании Eigenvector Research, Inc.

Многие книги и статьи содержат MatLab коды, позволяющие читателю сразу применить описываемые методы на практике. MatLab прекрасно интегрируется с Microsoft Word и Excel. Российское хемометрическое общество издало учебное пособие, являющееся полезным введением в хемометрические приложения MatLab.

1. Базовые сведения

1.1. Рабочая среда MatLab

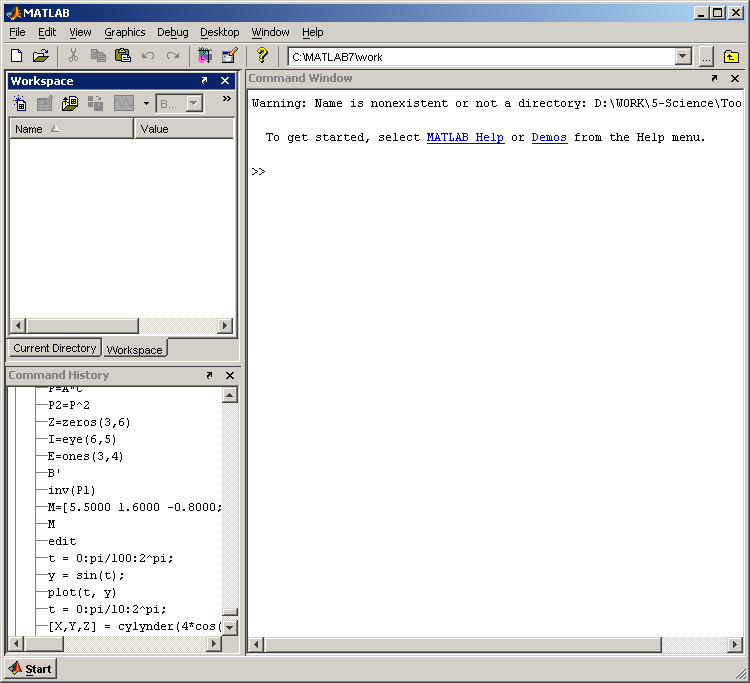
Чтобы запустить программу дважды щелкните на иконку . Перед Вами откроется рабочая среда, изображенная на рисунке.

Рабочая среда MatLab 6.х немного отличается от рабочей среды предыдущих версий, она имеет более удобный интерфейс для доступа ко многим вспомогательным элементам

Рабочая среда MatLab 6.х содержит следующие элементы:

панель инструментов с кнопками и раскрывающимся списком;

окно с вкладками Launch Pad и Workspace, из которого можно получить доступ к различным модулям ToolBox и к содержимому рабочей среды;

окно с вкладками Command History и Current Directory, предназначенное для просмотра и повторного вызова ранее введенных команд, а также для установки текущего каталога;

командное окно, в котором находится приглашение к вводу » и мигающий вертикальный курсор;

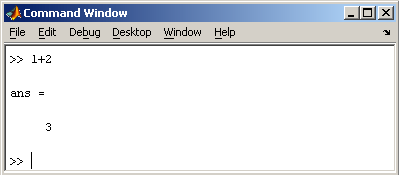
1.2. Простейшие вычисления

Рис. 2 Графическое представление метода главных компонент

Рис. 3 Графическое представление метода главных компонент

1.3. Эхо команд

Рис. 4 Пример ввода функции ScoresPCA

1.4. Сохранение рабочей среды. MAT файлы

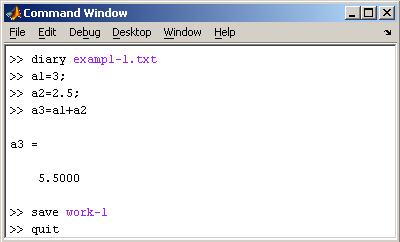
1.5. Журнал

производит следующие действия:

открывает журнал в файле exampl-1.txt ;

сохраняет все переменные в MAT файле work-1.mat ;

сохраняет журнал в файле exampl-1.txt в подкаталоге work корневого каталога MatLab и закрывает MatLab;

Посмотрите содержимое файла exampl-1.txt в каком-нибудь текстовом редакторе. В файле окажется следующий текст:

1.6. Система помощи

2. Матрицы

2.1. Скаляры, векторы и матрицы

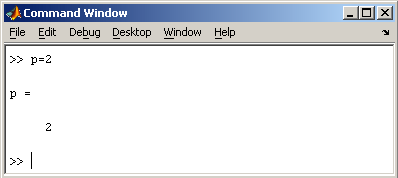
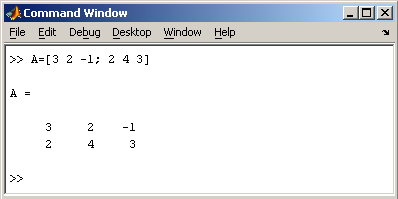
В MatLab можно использовать скаляры, векторы и матрицы. Для ввода скаляра достаточно приписать его значение какой-то переменной, например

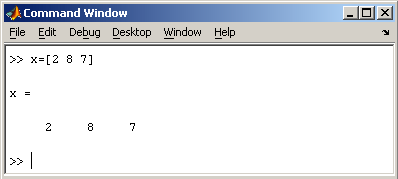
Заметим, что MatLab различает заглавные и прописные буквы, так что p и P — это разные переменные. Для ввода массивов (векторов или матриц) их элементы заключают в квадратные скобки. Так для ввода вектора-строки размером 1×3, используется следующая команда, в которой элементы строки отделяются пробелами или запятыми.

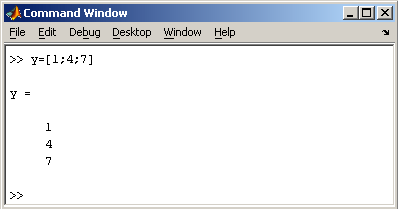
При вводе вектора-столбца элементы разделяют точкой с запятой. Например,

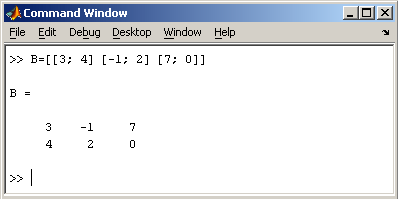
Вводить небольшие по размеру матрицы удобно прямо из командной строки. При вводе матрицу можно рассматривать как вектор-столбец, каждый элемент которого является вектором-строкой.

или матрицу можно трактовать как вектор строку, каждый элемент которой является вектором-столбцом.

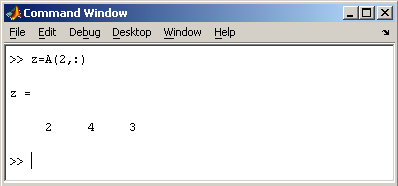
2.2. Доступ к элементам

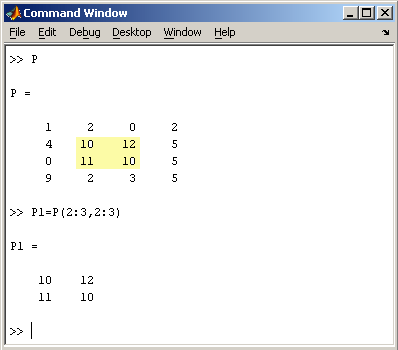
Также можно осуществлять выделение блоков матриц при помощи двоеточия. Например, выделим из матрицы P блок отмеченный цветом

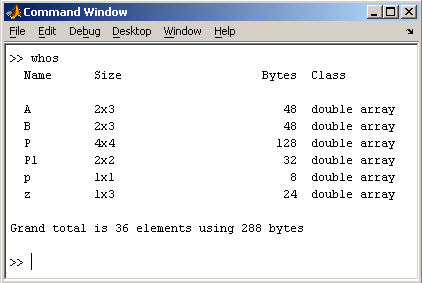
Видно, что в рабочей среде содержатся один скаляр ( p ), четыре матрицы ( A, B, P, P1 ) и вектор-строка ( z ).

2.3. Основные матричные операции

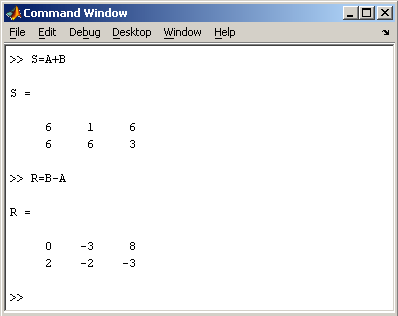
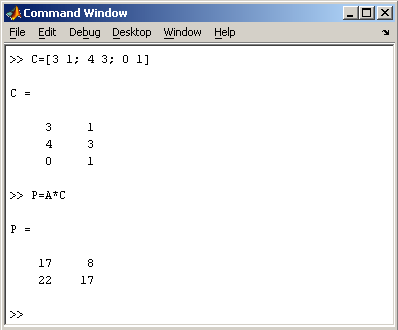
При использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус

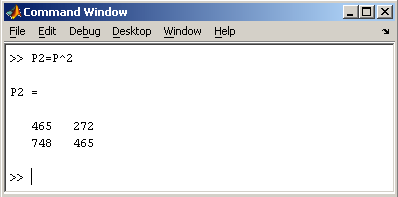
Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева. Возведение квадратной матрицы в целую степень производится с использованием оператора ^

Проверьте полученный результат, умножив матрицу Р саму на себя.

2.4. Создание матриц специального вида

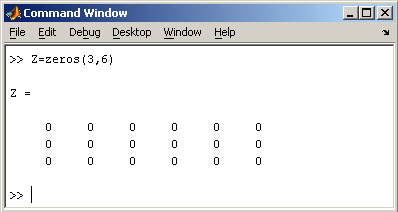
Заполнение прямоугольной матрицы нулями производится встроенной функцией zeros

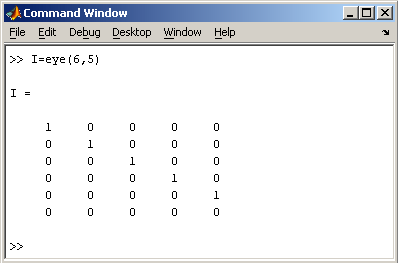
Единичная матрица создается при помощи функции eye

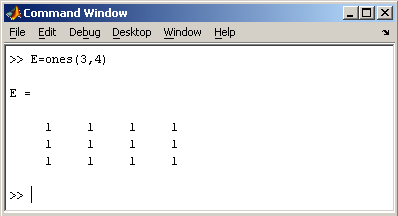
Матрица, состоящая из единиц, образуется в результате вызова функции ones

MatLab предоставляет возможность заполнения матриц случайными числами. Результатом функции rand является матрица чисел, равномерно распределенных между нулем и единицей, а функции randn — матрица чисел, распределенных по нормальному закону с нулевым средним и единичной дисперсией.

Функция diag формирует диагональную матрицу из вектора, располагая элементы по диагонали.

2.5. Матричные вычисления

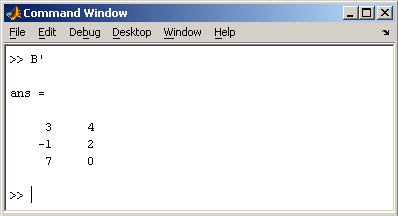
MatLab содержит множество различных функций для работы с матрицами. Так, например, транспонирование матрицы производится при помощи апострофа ‘

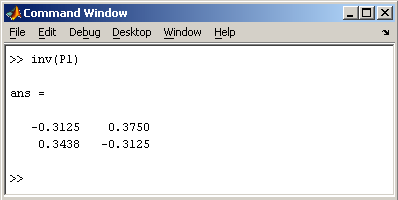
Нахождение обратной матрицы проводится с помощью функции inv для квадратных матриц

3. Интегрирование MatLab и Excel

Интегрирование MatLab и Excel позволяет пользователю Excel обращаться к многочисленным функциям MatLab для обработки данных, различных вычислений и визуализации результата. Надстройка excllink.xla реализует данное расширение возможностей Excel. Для связи MatLab и Excel определены специальные функции.

3.1. Конфигурирование Excel

3.2. Обмен данными между MatLab и Excel

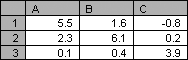
Запустите Excel, проверьте, что проделаны все необходимые настройки так, как описано в предыдущем разделе (MatLab должен быть закрыт). Введите в ячейки с A1 по C3 матрицу, для отделения десятичных знаков используйте точку в соответствии с требованиями Excel.

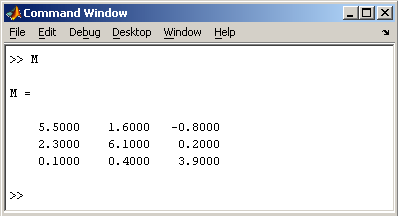
Результат аналогичен полученному при выполнении команды в среде MatLab.

Итак, для экспорта матрицы в MatLab следует выделить подходящие ячейки листа Excel, а для импорта достаточно указать одну ячейку, которая будет являться верхним левым элементом импортируемого массива. Остальные элементы запишутся в ячейки листа согласно размерам массива, переписывая содержащиеся в них данные, поэтому следует соблюдать осторожность при импорте массивов.

4. Программирование

4.1. М-файлы

Работа из командной строки MatLab затрудняется, если требуется вводить много команд и часто их изменять. Ведение дневника при помощи команды diary и сохранение рабочей среды незначительно облегчают работу. Самым удобным способом выполнения групп команд MatLab является использование М-файлов, в которых можно набирать команды, выполнять их все сразу или частями, сохранять в файле и использовать в дальнейшем. Для работы с М-файлами предназначен редактор М-файлов. С его помощью можно создавать собственные функции и вызывать их, в том числе и из командного окна.

М-файлы в MatLab бывают двух типов: файл-программы (Script M-Files), содержащие последовательность команд, и файл-функции, (Function M-Files), в которых описываются функции, определяемые пользователем.

4.2. Файл-программа

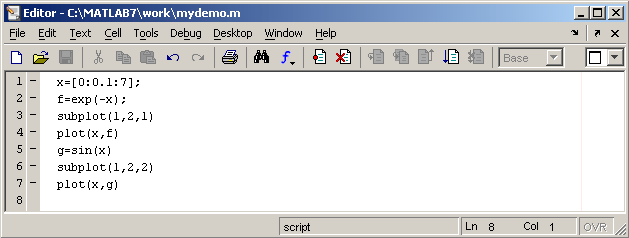
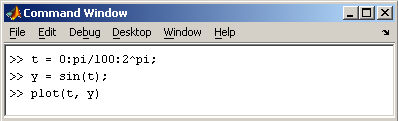
Наберите в редакторе команды, приводящие к построению двух графиков на одном графическом окне

Команды файл-программы осуществляют вывод в командное окно. Для подавления вывода следует завершать команды точкой с запятой. Если при наборе сделана ошибка и MatLab не может распознать команду, то происходит выполнение команд до неправильно введенной, после чего выводится сообщение об ошибки в командное окно.

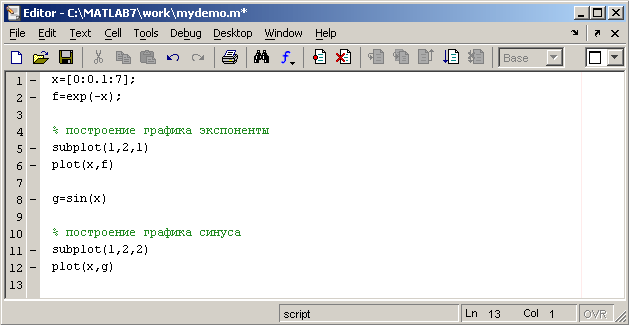
Отдельные блоки М-файла можно снабжать комментариями, которые пропускаются при выполнении, но удобны при работе с М-файлом. Комментарии начинаются со знака процента и автоматически выделяются зеленым цветом, например:

Открытие существующего М-файла производится при помощи пункта Open меню File рабочей среды, либо редактора М-файлов.

4.3. Файл-функция

Рассмотренная выше файл-программа является только последовательностью команд MatLab, она не имеет входных и выходных аргументов. Для использования численных методов и при программировании собственных приложений в MatLab необходимо уметь составлять файл-функции, которые производят необходимые действия с входными аргументами и возвращают результат действия в выходных аргументах. Разберем несколько простых примеров, позволяющих понять работу с файл-функциями.

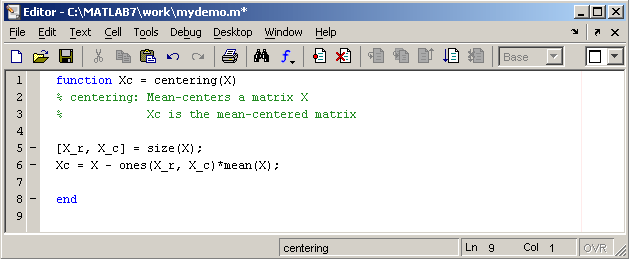
Проводя предобработку данных многомерного анализа хемометрики часто применяет центрирование. Имеет смысл один раз написать файл-функцию, а потом вызывать его всюду, где необходимо производить центрирование. Откройте в редакторе М-файлов новый файл и наберите

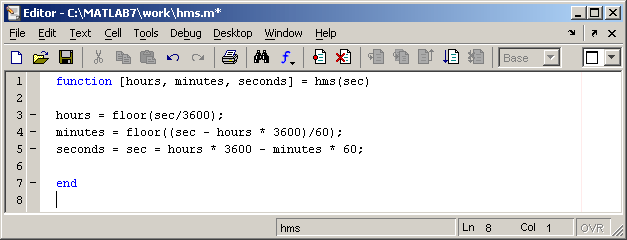
Можно написать файл-функции с несколькими входными аргументами, которые размещаются в списке через запятую. Можно также создавать и функции, возвращающие несколько значений. Для этого выходные аргументы добавляются через запятую в список выходных аргументов, а сам список заключается в квадратные скобки. Хорошим примером является функция, переводящая время, заданное в секундах, в часы, минуты и секунды.

При вызове файл-функций с несколькими выходными аргументами результат следует записывать в вектор соответствующей длины.

4.4 Создание графика

MatLab имеет широкие возможности для графического изображения векторов и матриц, а также для создания комментариев и печати графиков. Дадим описание несколько важных графических функций.

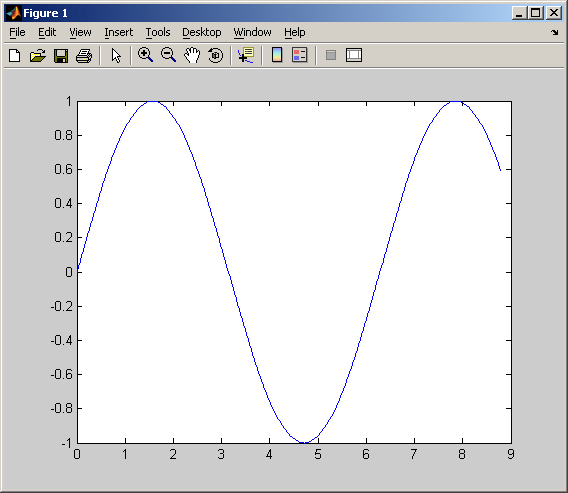
Программа построила график зависимости, который отображается в окне Figure 1

MatLab автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает пользователь), что позволяет различать наборы данных.

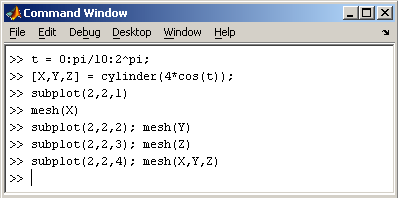
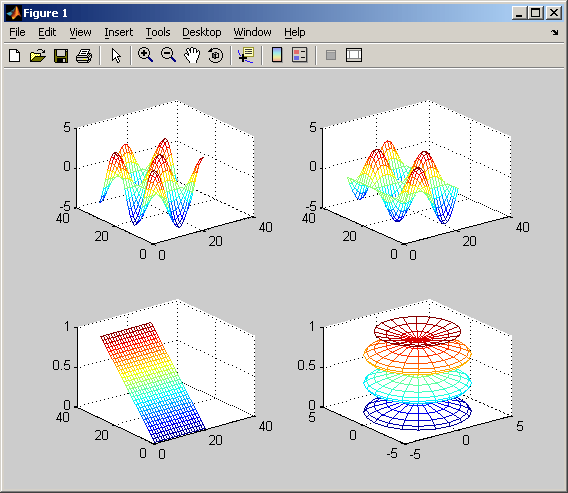
Команда hold on позволяет добавлять кривые на существующий график. Функция subplot позволяет выводить множество графиков в одном окне

4.5 Печать графиков

Пункт Print в меню File и команда print печатают графику MatLab. Меню Print вызывает диалоговое окно, которое позволяет выбирать общие стандартные варианты печати. Команда print обеспечивает большую гибкость при выводе выходных данных и позволяет контролировать печать из М-файлов. Результат может быть послан прямо на принтер, выбранный по умолчанию, или сохранен в заданном файле.

5. Примеры программ

В этом разделе приведены наиболее употребительные алгоритмы, используемые при анализе многомерных данных. Рассмотрены как простейшие методы преобразования данных центрирование и шкалирование, так и алгоритмы для анализа данных — PCA, PLS.

5.1. Центрирование и шкалирование

Часто при анализе требуется преобразовать исходные данные. Наиболее используемыми методами преобразования данных выступают центрирование и шкалирование каждой переменной на стандартное отклонение. В разделе 4.3 приводился код функции для центрирования матрицы. Поэтому ниже показан только код функции, которая шкалирует данные. Обратите внимание, что исходная матрица должна быть центрирована

function Xs = scaling(X)
% scaling: the output matrix is Xs
% matrix X must be centered

Xs = X * inv(diag(std(X)));

5.2. SVD/PCA

Наиболее популярным способом сжатия данных в многомерном анализе является метод главных компонент (PCA). С математической точки зрения PCA — это декомпозиция исходной матрицы X, т.е. представление ее в виде произведения двух матриц T и P

function [T, P] = pcasvd(X)
% pcasvd: calculates PCA components.
% The output matrices are T and P.
% T contains scores
% P contains loadings

[U,D,V] = svd(X);
T = U * D;
P = V;

5.3 PCA/NIPALS

Для построения PCA счетов и нагрузок, используется рекуррентный алгоритм NIPALS, который на каждом шагу вычисляет одну компоненту. Сначала исходная матрица X преобразуется (как минимум – центрируется; см. раздел 4.3) и превращается в матрицу E₀, a=0. Далее применяют следующий алгоритм.

После вычисления очередной (a-ой) компоненты, полагаем t_a=t и p_a=p. Для получения следующей компоненты надо вычислить остатки E_a+1 = E_a – t p t и применить к ним тот же алгоритм, заменив индекс a на a+1.

Код алгоритма NIPALS может быть написан и самими читателями, в данном же пособии авторы приводят свой вариант. При расчете PCA, можно вводить число главных компонент (переменная numberPC ). Если же не известно, сколько необходимо компонент, следует написать в командной строке [P,T] = pcanipals (X) и тогда программа задаст число компонент равным наименьшему из показателей размерности исходной матрицы X.

function [T, P] = pcanipals(X, numberPC)
% pcanipals: calculates PCA components.
% The output matrices are T and P.
% T contains scores
% P contains loadings

% calculation of number of components
[X_r, X_c] = size(X); P=[]; T=[];

if lenfth(numberPC) > 0
pc = numberPC<1>;
elseif (length(numberPC) == 0) & X_r pc = X_r;
else
pc = X_c;
end;

% calculation of scores and loadings for each component
for k = 1:pc
P1 = rand(X_c, 1); T1 = X * P1; d0 = T1’*T1;
P1 = (T1′ * X/(T1′ * T1))’; P1 = P1/norm(P1); T1 = X * P1; d = T1′ * T1;

О вычислении PCA с помощью надстройки Chemometrics рассказано в пособии Проекционные методы в системе Excel.

5.4 PLS1

Самым популярным способом для многомерной калибровки является метод проекции на латентные структуры (PLS). В этом методе проводится одновременная декомпозиция матрицы предикторов X и матрицы откликов Y:

Детальное описание метода PLS приведено в этой книге Для построения PLS1 счетов и нагрузок, используется рекуррентный алгоритм. Сначала исходные матрицы X и Y центрируют

и они превращаются в матрицу E₀ и вектор f₀, a=0. Далее к ним применяет следующий алгоритм

Приведем код этого алгоритма, взятый из книги

function [w, t, u, q, p] = pls(x, y)
%PLS: calculates a PLS component.
%The output vectors are w, t, u, q and p.
%
% Choose a vector from y as starting vector u.

u = y(:, 1);

% The convergence criterion is set very high.
kri = 100;

% Each starting vector u is saved as uold.
uold = u; w = (u’ * x)’; w = w/norm(w);
t = x * w; q = (t’ * y)’/(t’ * t);
u = y * q/(q’ * q);

% After convergence, calculate p.
p = (t’ * x)’/(t’ * t);

О вычислении PLS1 с помощью надстройки Chemometrics Add In рассказано в пособии Проекционные методы в системе Excel.

5.5 PLS2

Для PLS2 алгоритм выглядит следующим образом. Сначала исходные матрицы X и Y преобразуют (как минимум – центрируют; см. разделе 4.3), и они превращаются в матрицы E₀ и F₀, a=0. Далее к ним применяет следующий алгоритм.

Приведем код, которой также заимствован из из книги.

function [W, T, U, Q, P, B, SS] = plsr(x, y, a)
% PLS: calculates a PLS component.
% The output matrices are W, T, U, Q and P.
% B contains the regression coefficients and SS the sums of
% squares for the residuals.
% a is the numbers of components.
%
% For a components: use all commands to end.

for i=1:a
% Calculate the sum of squares. Use the function ss.
sx = [sx; ss(x)];
sy = [sy; ss(y)];

% Use the function pls to calculate one component.
[w, t, u, q, p] = pls(x, y);

% Save the vectors in matrices.
W = [W w];
T = [T t];
U = [U u];
Q = [Q q];
P = [P p];
end;

% Calculate the regression coefficients after the loop.
B=W*inv(P’*W)*Q’;

% Add the final residual SS to the sum of squares vectors.
sx=[sx; ss(x)];
sy=[sy; ss(y)];

% Make a matrix of the ss vectors for X and Y.
SS = [sx sy];

function [ss] = ss(x)
%SS: calculates the sum of squares of a matrix X.
%
ss=sum(sum(x. * x));
%End of ss

О вычислении PLS2 с помощью надстройки Chemometrics Add In рассказано в пособии Проекционные методы в системе Excel.

Заключение

MatLab это это очень популярный инструмент для анализа данных. По данным опроса, его используют до трети всех исследователей, тогда как программа the Unsrambler применяется только 16% ученых. Главным недостатком MatLab являются его высокая цена. Кроме того, MatLab хорош для рутинных расчетов. Отсутствие интерактивности делает его неудобным при выполнении поисковых, исследовательских расчетов для новых, неисследованных массивов данных.