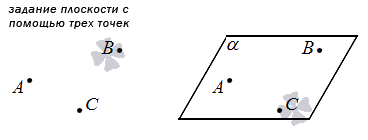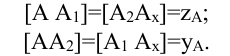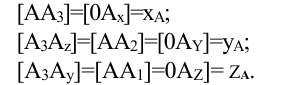Обозначения и символика
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
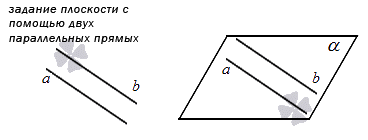
α(а || b) — плоскость α определяется параллельными прямыми а и b;
5. Углы обозначаются:
6. Угловая: величина (градусная мера) обозначается знаком 


Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
π2 —фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3. n:
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
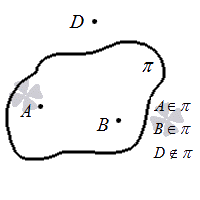
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
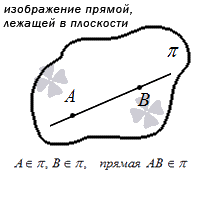
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
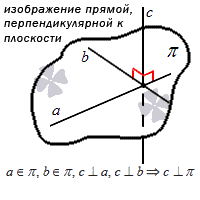
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Графически этот вариант расположения выглядит так:
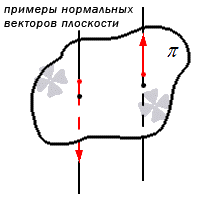
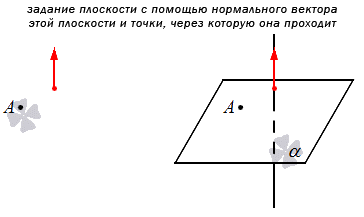
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
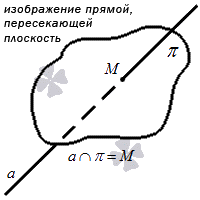
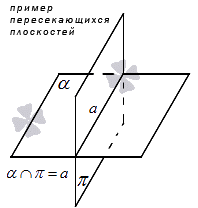
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
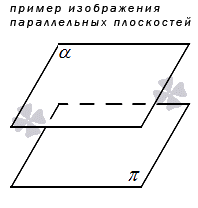
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
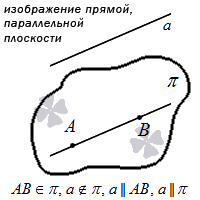
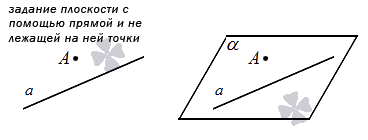
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
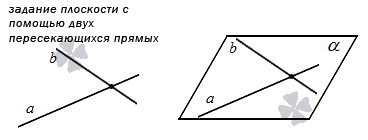
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
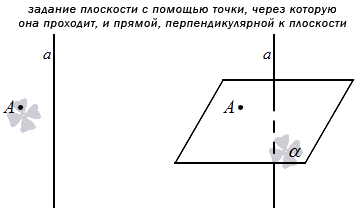
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.
Плоскость
Понятие плоскости
поверхность школьной доски:
Эти поверхности ограничены, у них есть края. Но представление о плоскости мы имеем с их помощью.
Только плоскость простирается безгранично (в любом направлении, заданном на этой плоскости).
Понятие плоскость принадлежит к числу основных понятий геометрии.
Обозначение плоскости
Конечно, нарисовать плоскость, у которой нет краев, невозможно. Поэтому, при изображении плоскости, рисуют только ее часть:
Обозначается плоскость строчными буквами греческого алфавита – α (альфа), β (бета), γ (гамма) и т.д.:
Буквы пишут либо рядом с плоскостью, либо на плоскости.
Определение плоскости
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки. ( то есть, любая прямая, соединяющая две ее точки, целиком принадлежит ей).
Поделись с друзьями в социальных сетях:
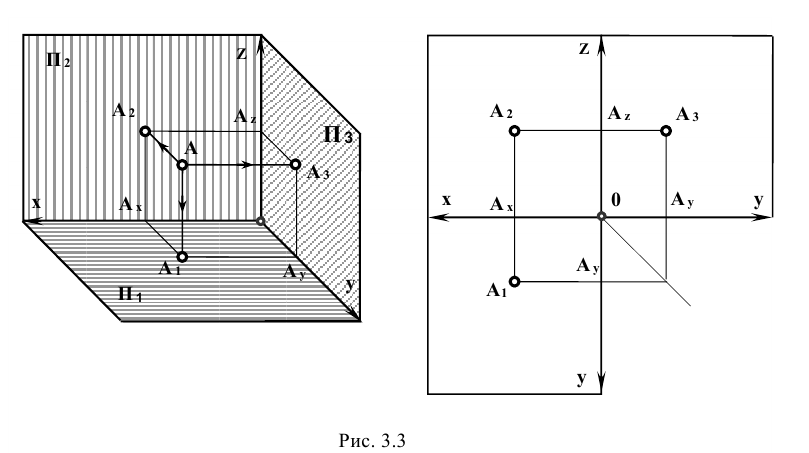
Проецирование точки в начертательной геометрии с примерами
Проецирование точки на две и три плоскости проекций:
Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций
Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки А:
Плоскость прямоугольника 
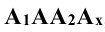
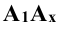
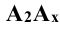
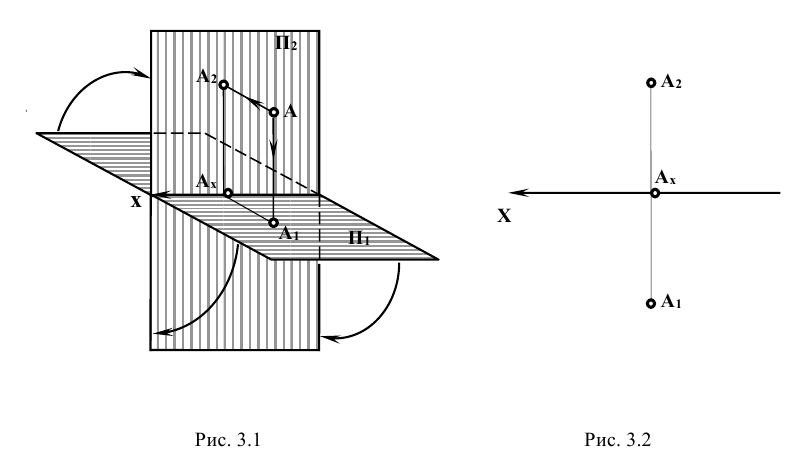
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость 
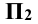
Проекции 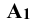
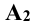
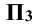
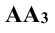
Для получения плоского чертежа в этом случае уже две плоскости 
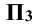
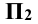
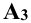
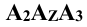
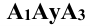
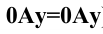
Это не означает, что модули этих величин обязательно равны между собой, т.е. 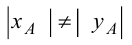
Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.
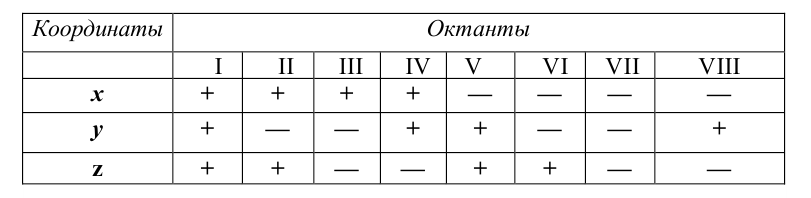
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например А, принадлежит:
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А принадлежит:
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Так, точка А лежит на оси х, если 
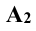
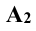
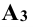
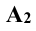
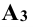
Правила знаков координат проекции точки
При построении проекции точки координата x всегда откладывается от начала координат (точка 0).
Таблица 3.1
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.