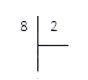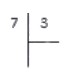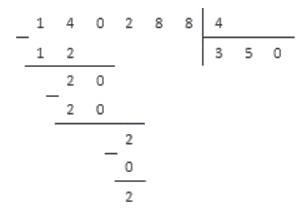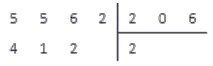Блог молодого админа
Увлекательный блог увлеченного айтишника
Знак деления на клавиатуре компьютера или ноутбука: как поставить?
Если вы печатаете с помощью клавиатуры своего компьютера или ноутбука математические примеры, то можете все символы набрать на самой клавиатуре. Не верите? В этой статье мы покажем пример со знаком деления. Способов будет несколько. Какой из них использовать, решать вам. Начнем с наиболее простого.
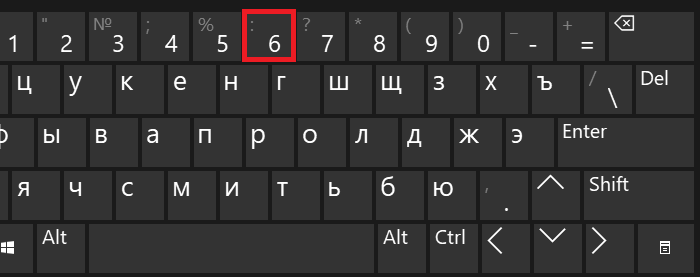
Двоеточие
Надо отметить, что знаком деления могут выступать различные символы. Один из них — это двоеточие, находится он на той же клавише, что и цифра 6.
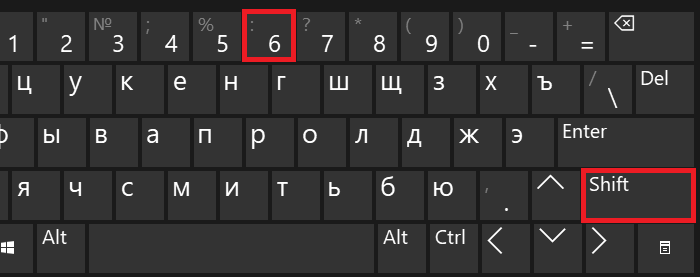
Чтобы поставить этот знак, нужно нажать на Shift и, удерживая клавишу, нажать на клавишу 6, после чего отпустить Shift.
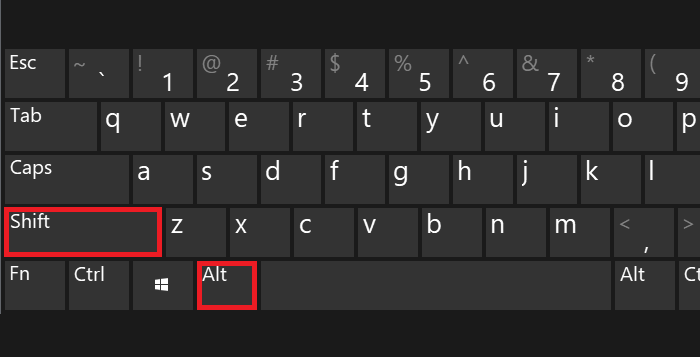
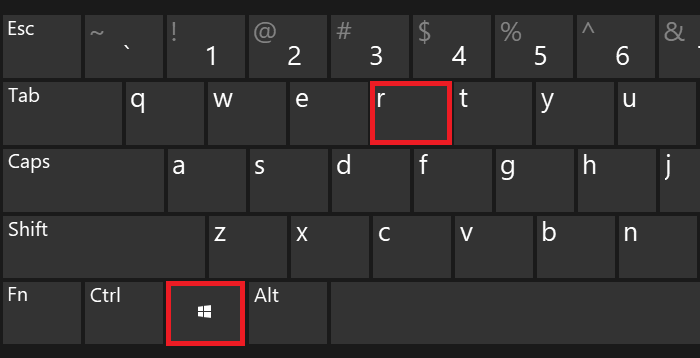
Если вы вдруг увидели другой символ, это говорит о том, что у вас используется англоязычная раскладка. Переключите ее на русскоязычную, нажав на клавиши Shift+Ctrl:
Можете также воспользоваться Alt-кодом. Для этого зажмите Alt и, удерживая его, наберите цифры 58, после чего отпустите Alt.
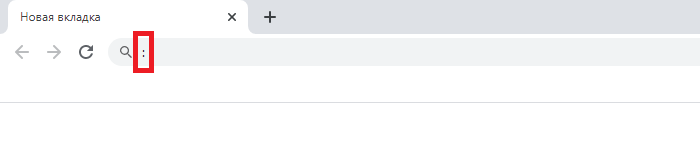
Если все сделано верно, вы увидите двоеточие.
Если не получилось с правым Alt, используйте левый.
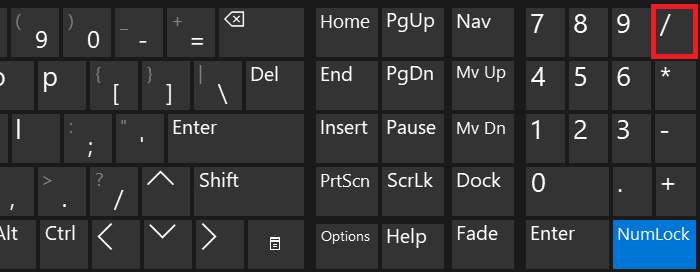
Косая черта
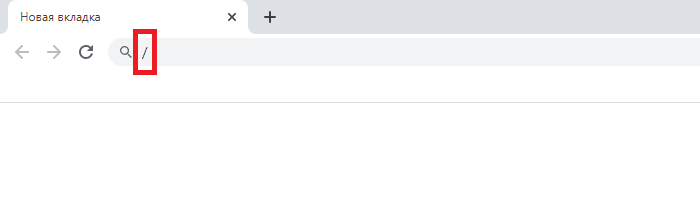
В качестве знака деления может выступать косая черта. Она находится рядом с цифровой клавиатурой.
Просто нажмите на нее один раз.
Что должно получиться:
Раскладка клавиатуры роли не играет.
Alt-код для косой черты — 47:
Символ умножения из таблицы символов
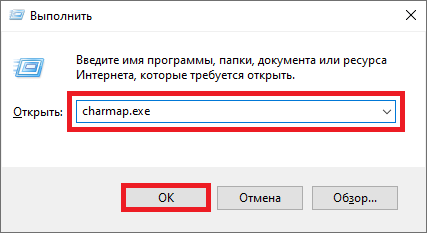
Можете использовать таблицу символов Windows, чтобы указать обелюс (знак деления), который обычно встречается на калькуляторах.
Затем в окно «Выполнить» введите команду charmap.exe и кликните ОК.
Если все сделали верно, увидите таблицу символов Windows.
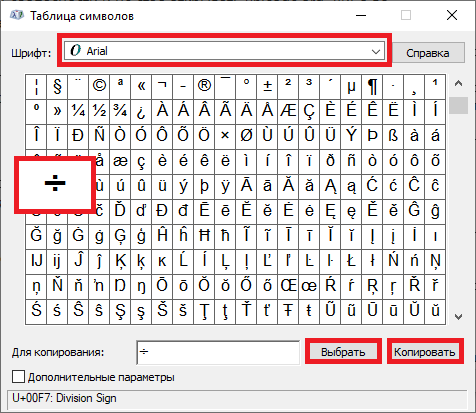
Выбираете шрифт Arial, находите символ деления, кликаете по нему, после чего кликаете по кнопкам «Выбрать» и «Копировать».
Можно использовать и Alt-коды.
В данном случае нужно набрать цифры 0247 на цифровой клавиатуре (англоязычная раскладка).
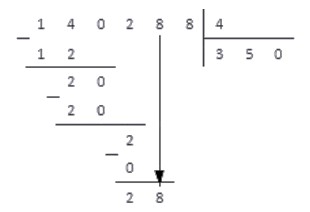
Деление натуральных чисел столбиком: правило, примеры
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Запись чисел при делении столбиком
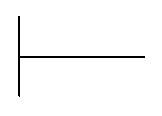
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
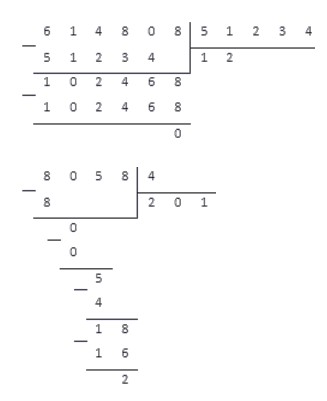
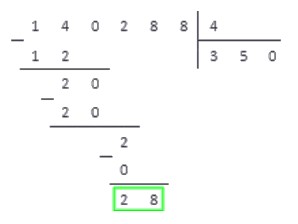
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
3 · 0 = 0 7 ; 3 · 1 = 3 7 ; 3 · 2 = 6 7 ; 3 · 3 = 9 > 7
В завершение операции вычитаем 6 из 7 и получаем:
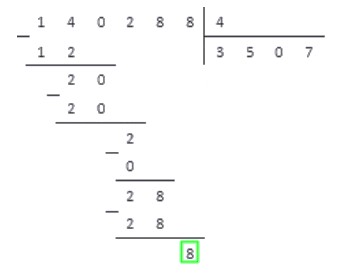
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком
В соответствии с алгоритмом имеем:
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
4 · 0 = 0 2 ; 4 · 1 = 4 > 2
3. Выполняем операцию вычитания и под чертой записываем результат.
Проделав все по правилам, получаем результат:
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
После второго, третьего и четвертого шага алгоритма запись примет вид:
Последний проход, и поучаем результат:
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Деление многозначных натуральных чисел столбиком
Рассмотрим применение алгоритма деления многозначных чисел на примере.
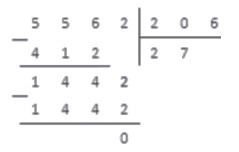
Пример 3. Деление натуральных чисел в столбик
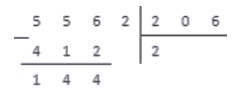
206 · 0 = 0 556 ; 206 · 1 = 206 556 ; 206 · 2 = 412 556 ; 206 · 3 = 618 > 556
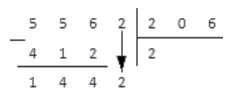
Выполняем вычитание столбиком
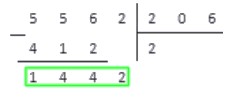
206 · 5 = 1030 1442 ; 206 · 6 = 1236 1442 ; 206 · 7 = 1442
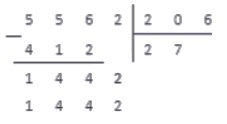
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
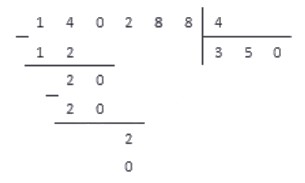
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Деление в столбик.
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида 
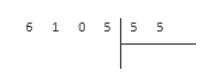
Например, если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
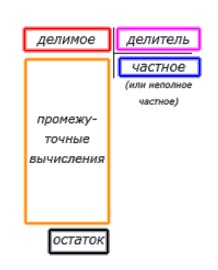
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.
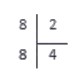
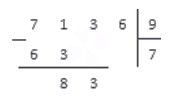
Как делить в столбик лучше всего объяснить на примере. Вычислить :
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
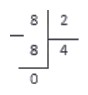
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
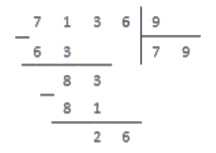
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
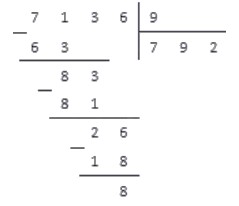
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2) ).
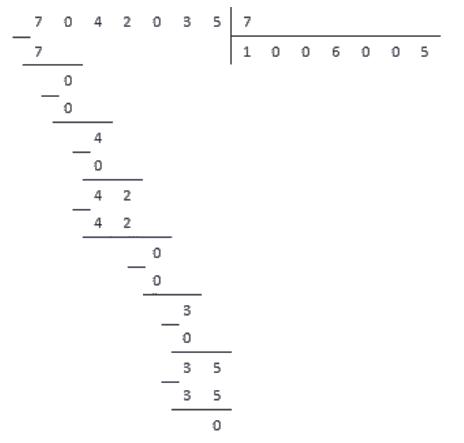
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое «промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Значит, 1976 : 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Десятичные дроби онлайн. Перевод десятичных дробей в обычные и обычных дробей в десятичные.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например, 64 разделим на 5.
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего, меньшего разряда и продолжать деление.
Как быстро научить ребенка делить столбиком?
Чтобы упростить деление чисел, традиционно используется метод деления в столбик. Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.
Как правильно делить в столбик?
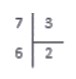
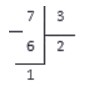
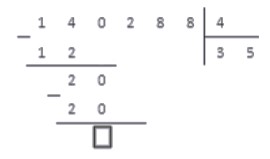
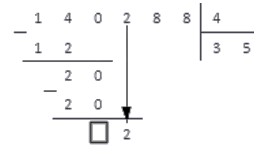
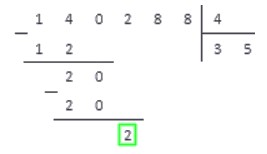
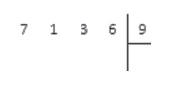
Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).
Как найти частное двух чисел – 35 и 5?
Что нужно знать ребенку для понимания деления столбиком?
Чтобы любимое чадо освоило, как делить уголком (в столбик), нужно два условия:
В конце 3 класса ученики усваивают, как разделить простые двузначные числа.
При переходе в 4 класс дети учатся делить многозначные числа (больше, чем 100). Также происходит обучение делению уголком чисел с двузначным и трехзначным делителем, решение примеров с остатком.
Методика обучения детей делению столбиком
Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.
Проверьте знание таблицы умножения. Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.
Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).
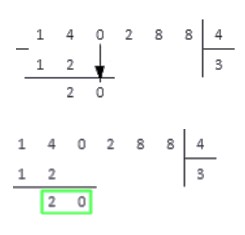
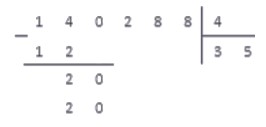
Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.
Работа с многозначными числами
Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:
Пример решен, можно проверить правильность путем умножения: 62X6=372.
Как объяснить деление с остатком?
Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:
В группе 8 учеников, на обед им выдали 18 ватрушек на подносе. Когда каждый получит по 2 ватрушки (18:8=2 и ост. 2), на подносе останутся лишние 2 штуки. Это и есть остаток.
Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).
Обучение школьника должно проходить поэтапно, от простых примеров к более сложным. Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.
Поиск ответа
| Вопрос № 287655 |
Пожалуйста, как правильно указать ЧЕТЫРЕХзна чное число (с запятой или без) при такой единице измерения: площадь жилого фонда составляет 1522 тыс. кв. м или все же 1,522 тыс. кв. м
Ответ справочной службы русского языка
В русском языке разделительная запятая ставится в дробных числах. Целые числа пишутся без запятых: . составляет 1522 тыс. кв. м.
Подскажите, исходя из какого правила требуется запятая в предложении ниже. В настоящем справочнике многозначные целые числа (включая четырехзна чные) разбиты на группы в соответствии с «Основными математическими обозначениями», как документом более высокого значения.
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Добрый день! Почти месяц назад интересовалась, но ответа не получила.
«Вопрос № 265302
Уважаемая Грамота,
Подскажите, пожалуйста, как правильно писать четырехзна чные числа типа:
4 515 товаров
7 500 об/мин
1 500 тыс. руб.
Верна ли постановка пробела?
Ответ справочной службы русского языка
Да, пробел нужен. Технические правила набора дают указание разбивать на группы многозначные числа начиная с 4-значных (по три цифры справа налево). «
Однако нашлось три источника, которые утверждают, что «пробел ставится, начиная с пятизначных чисел»:
Наборные и фотонаборные процессы, М-, 1983, п. 2.3.9
Гиленсон. Справочник художественного и технического редакторов
http://www.artlebedev.ru/kovodstvo/sections/74/
Как же правильно и кому верить?
Ответ справочной службы русского языка
Числа в цифровой форме делят пробелами на группы (по три цифры) справа налево. Технические правила набора дают указание разбивать на группы числа только начиная с 5-значных (см. Наборные и фотонаборные процессы, М., 1983, п. 2.3.9), а «Основные математические обозначения (СЭВ PC 2625—70)» не делают исключения и для 4-значных чисел.
Не разбиваются на группы цифры в числах, обозначающих номер (после знака номера), в марках машин и механизмов, в обозначениях нормативных документов (стандарты, техн. условия). Например: № 89954.
Точку в пробелах между цифровыми группами многозначного числа ставить запрещается.
(А. Э. Мильчин, Л. К. Чельцова, Справочник издателя и автора)
Подскажите, пожалуйста, как правильно писать четырехзна чные числа типа:
4 515 товаров
7 500 об/мин
1 500 тыс. руб.
Верна ли постановка пробела?
Ответ справочной службы русского языка
Да, пробел нужен. Технические правила набора дают указание разбивать на группы многозначные числа начиная с 4-значных (по три цифры справа налево).
Ответ справочной службы русского языка
Предпочтительно: _4 000_. Верно: _С. Петрова_.
Скажите, пожалуйста, нужно ли использовать пробел в четырехзна чном числительном: 4 500, 1500? Спасибо.
Ответ справочной службы русского языка