Знак пересечения
Определение
Знак пересечения – это символ, указывающий на пересечение прямых, углов, лучей, отрезков, плоскостей и других фигур в геометрии, пересечение множеств в математике (алгебре) и информатике.
Как пишется этот символ пересечения?
Этот знак выглядит и пишется так – ⋂
Его достаточно легко запомнить, он похож на русскую букву «П», начальную букву слова «пересечение».
Как быстро запомнить этот знак?
Просто представьте себе и запомните, что этот символ выглядит как буква «П» и похож на подкову, перевернутую вниз ногами.
Как применяется знак ⋂?
Применяется для обозначения пересечения прямых, углов, лучей, отрезков в геометрии, пересечение множеств в математике (алгебре) и информатике.
Как выглядит знак «не пересечения» в геометрии?
Пример
А ∩ С = ∅ — 2 луча или (2 прямые, 2отрезка) А и С не пересекаются.
Что обозначает знак пересечения наоборот?
Это символ выглядит и пишется следующим образом: ∪
Обозначается термином – «объединение».
Знаки, обозначающие взаимное расположение объектов
|| – знак параллельности;
≡ – знак совпадения (тождества);
∩– знак пересечения двух геометрических элементов;
= – знак результата геометрического построения;
∟ – знак прямого угла;
Δ – знак треугольника;
∈ – знак принадлежности одного геометрического элемента другому;
A ∈ (ВС) – точка А принадлежит прямой ВС;
С – знак включения, А ∈ Н – прямая А принадлежит плоскости Н;
∩ – знак пересечения, А ∩ Н – прямая А пересекает плоскость Н;
=> – импликация – логическое следствие; означает «если, то …».
ТОЧКА
Метод проекций
В основе правил построения изображений лежит метод проекций. Суть метода заключается в том, что каждой точке трехмерного пространства соответствует определенная точка двухмерного пространства плоскости. Изучение его начинают с построений проекций точки, т. к. любой геометрический объект может рассматриваться как множество точек, заданных по определенному закону. Этот геометрический объект отображается на плоскость по закону проецирования. Процесс отображения называется проецированием. Результатом такого отображения является изображение объекта, которое называется проекцией.
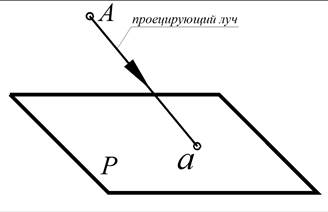
Для построения проекции геометрического объекта задают аппарат проецирования, в который входит объект проецирования,например, точка А,и плоскость проецирования Р (иногда ее называют картинной плоскостью), не проходящая через точку А (рис. 1).Для получения изображения точки А на плоскость Р через нее проводят проецирующий луч до его пересечения с плоскостью Р в точке а. Полученную точку а называют проекцией точки А. Проекция (лат. projectio – выбрасывание вперед).
Рис. 1. Проецирование точки А
Виды проецирования
Задан аппарат проецирования: центр проекций S, плоскость проецирования Р.
В результате центрального проецирования на плоскости Р получится центральная проекция любого геометрического объекта. На рис. 2 показано построение центральной проекции отрезка АВ. Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой S (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Таким образом получаем на плоскости перспективное изображение предмета или центральную проекцию.
Свойства центральных проекций:
– проекция точки – точка;
– проекция прямой – прямая;
– если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.
2. Параллельное проецирование – частный случай центрального проецирования, когда центр проецирования бесконечно удален. Поэтому в аппарат проецирования входит: направление проецирования S и плоскость проецирования Р. При этом проецирующие лучи рассматривают как прямые, параллельные между собой и параллельные заданному направлению проецирования S (рис. 3).
Рис. 2. Центральное проецирование отрезка АВ
|
|
Рис. 3. Параллельное проецирование:
а – косоугольное отрезка АВ; б – ортогональное точки А
В зависимости от направления проецирования параллельные проекции могу быть:
– ортогональными (прямоугольными) проекциями – проекционные лучи падают перпендикулярно к картинной плоскости Р (рис. 3б);
– косоугольная проекция – проекционные лучи падают не перпендикулярно к картинной плоскости Р (рис. 3а).
Свойства параллельных проекций:
– проекция точки – точка;
– проекция прямой – прямая;
– если точка принадлежит прямой, то проекция этой точки принадлежит проекции этой же прямой;
– проекции параллельных прямых параллельны;
– отношение отрезков прямой равно отношению их проекций.
Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием:
– простота построений изображения геометрического объекта;
– точность – сохранение точных форм и размеров проецируемой фигуры на чертеже;
– наглядность –чертеж должен создавать пространственное представление о форме геометрического объекта;
– обратимость – возможностьвосстановления оригинала по проекционным изображениям геометрического объекта.