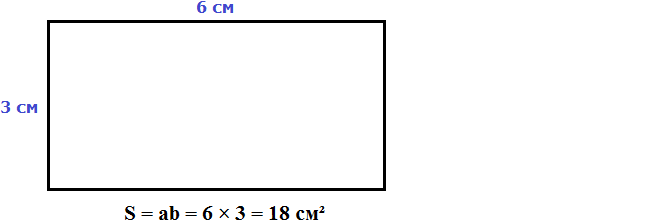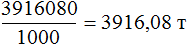Периметр
Периметр — это сумма длин всех сторон многоугольника.
Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».
Периметр измеряется в единицах длины: мм, см, м, км и т.д.
При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».
Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.
AB = 3 см, BC = 7 см
PABCD = (AB + BC) · 2
PABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».
KE = 7 см
PEKFM = 4 · KE
PEKFM = 4 · 7 = 28 (см)
Как найти периметр многоугольника
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.
PABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)
Как найти периметр фигуры
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.
P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
Какой буквой обозначается периметр в геометрии?
Практически каждый раз при решении задач по математике, физике или другим дисциплинам приходится выбирать обозначения тех или иных величин. Среди них следует различать обозначения общепринятые (или даже устанавливаемые нормативными документами) и обозначения, выбор которых обычно выполняется самостоятельно, в зависимости от индивидуальных предпочтений. Есть также величины, обозначения которых в разных дисциплинах приняты свои. Есть обозначения международные, а есть – принятые различными в разных странах.
Как обозначается длина, ширина, высота, толщина, глубина
Обозначение длины в математике обычно зависит от того, какой объект в данном случае рассматривается: одномерный, двумерный или трехмерный. Если речь идёт об обозначении длины одномерного объекта (нити, проволоки и т. п.) или обозначении длины куска сортового проката (трубы, швеллера, двутавра и т. п.), то длина обычно обозначается буквой l (написанной курсивом, т. е. с наклоном, чтобы не было похоже на «единицу») или L. Если же речь идёт о двумерном объекте, в котором нужно обозначить не только длину, но и ширину, то обычно принимают одну из таких пар обозначений: a и b (а – длина, b — ширина), l и b (l – длина, b — ширина), l и h (l – длина, h — высота). Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов. Если же речь идёт о длине волны, то она обозначается строчной греческой буквой «лямбда».
Высота обозначается обычно буквой h (читается: [аш]). В технической литературе для обозначения высоты также используют букву Н (читается: [аш]). Этими же буквами (h, реже Н) обозначается глубина.
Толщина в физике обозначается либо строчной (маленькой) буквой s, либо греческой строчной буквой «дельта», с использованием (при необходимости) нижних индексов (обычно – числовых, соответствующих номеру слоя, т. е. 1, 2, 3, 4 и т. д.).
Вопросы «как в математике пишется длина», «как в математике пишется периметр», «как в математике пишется площадь» некорректны. Здесь уместно вместо слова «пишется» употребить слово «обозначается».
Периметр, площадь и объём
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
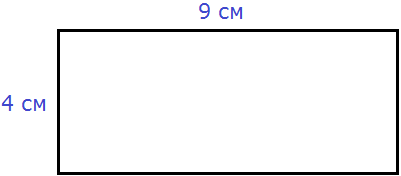
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
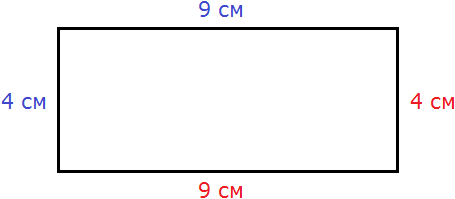
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters ). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
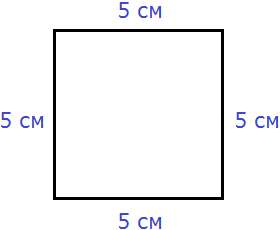
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
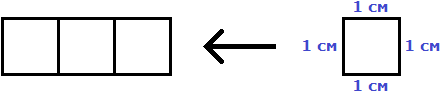
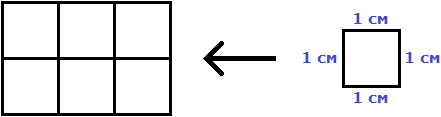
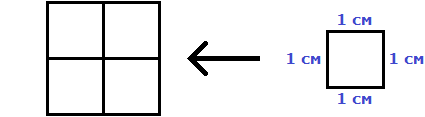
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
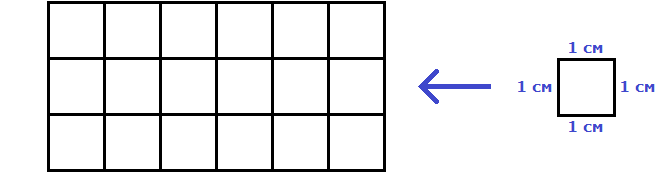
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
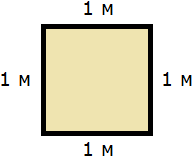
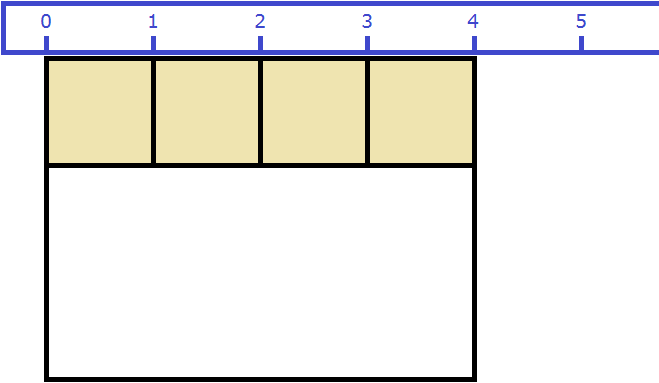
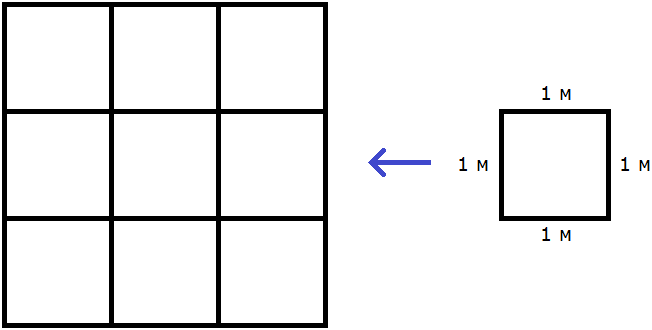
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
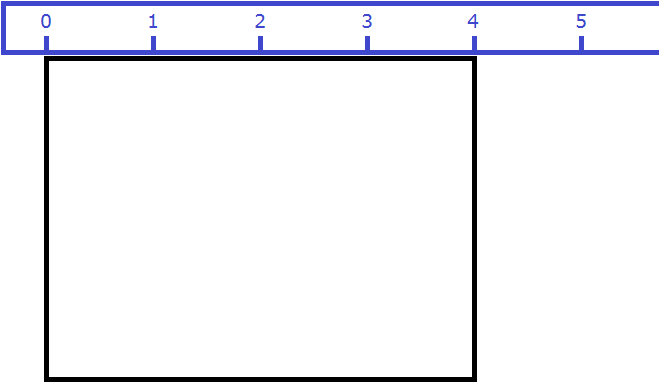
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
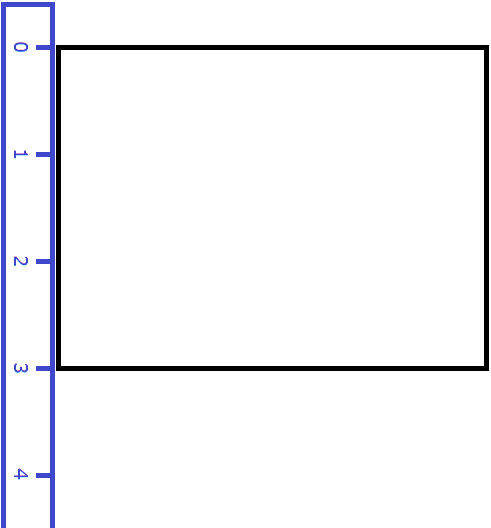
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
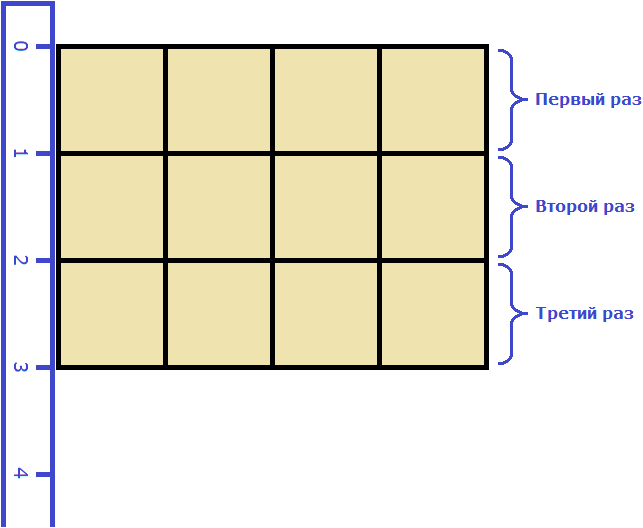
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
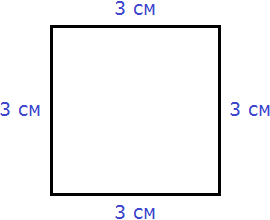
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
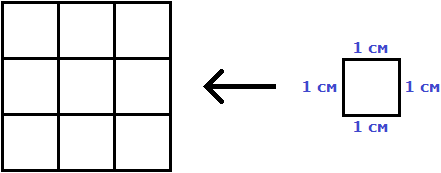
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
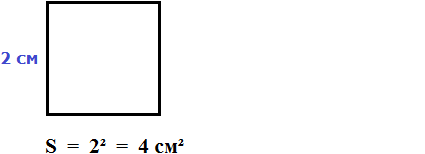
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
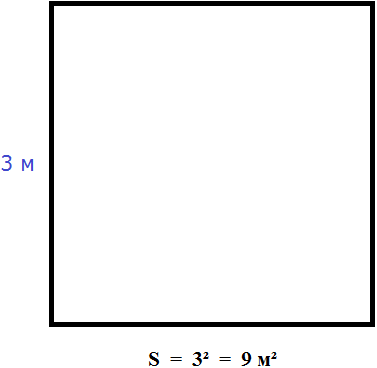
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
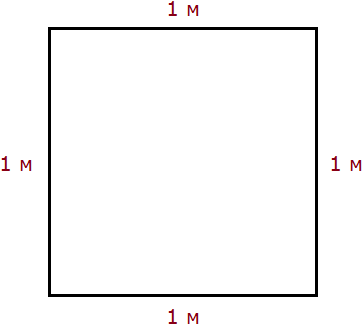
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
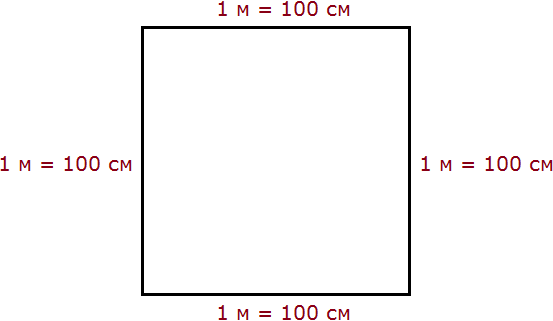
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 100 2 = 10 000 см 2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м 2 = 10 000 см 2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
Например, переведём 100 000 см 2 в квадратные метры. Рассуждать в этом случае можно так: « если 10 000 см 2 это один квадратный метр, то сколько раз 100 000 см 2 будут содержать по 10 000 см 2 »
100 000 см 2 : 10 000 см 2 = 10 м 2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км 2 в квадратные метры.
S = 1000 2 = 1 000 000 м 2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км 2 = 1 000 000 м 2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км 2 в квадратные метры. Умножим 2 км 2 на 1 000 000
2 км 2 × 1 000 000 = 2 000 000 м 2
Например, переведём 3 500 000 м 2 в квадратные километры. Рассуждать в этом случае можно так: « если 1 000 000 м 2 это один квадратный километр, то сколько раз 3 500 000 м 2 будут содержать по 1 000 000 м 2 »
3 500 000 м 2 : 1 000 000 м 2 = 3,5 км 2
Пример 2. Выразить 7 м 2 в квадратных сантиметрах.
Умножим 7 м 2 на 10 000
7 м 2 = 7 м 2 × 10 000 = 70 000 см 2
Пример 3. Выразить 5 м 2 13 см 2 в квадратных сантиметрах.
5 м 2 13 см 2 = 5 м 2 × 10 000 + 13 см 2 = 50 013 см 2
Пример 4. Выразить 550 000 см 2 в квадратных метрах.
550 000 см 2 : 10 000 см 2 = 55 м 2
Пример 5. Выразить 7 км 2 в квадратных метрах.
Умножим 7 км 2 на 1 000 000
7 км 2 × 1 000 000 = 7 000 000 м 2
Пример 6. Выразить 8 500 000 м 2 в квадратных километрах.
8 500 000 м 2 × 1 000 000 м 2 = 8,5 км 2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам ( 100 м 2 ). В виду частого распространения такой площади ( 100 м 2 ) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м 2 каждый, то есть:
3 а = 100 м 2 × 3 = 300 м 2
10 соток = 1000 м 2
20 га = 10 000 м 2 × 20 = 200 000 м 2
Прямоугольный параллелепипед и куб
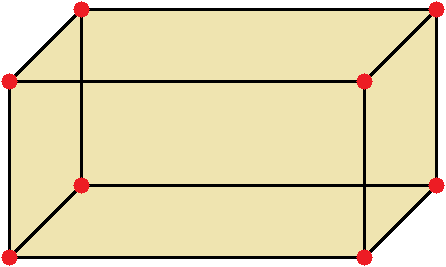
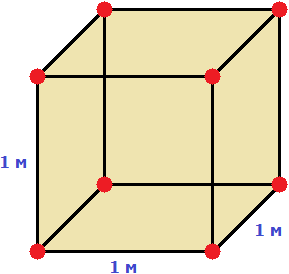
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
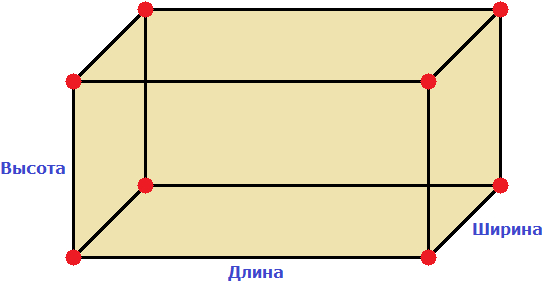
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
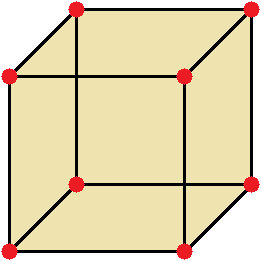
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
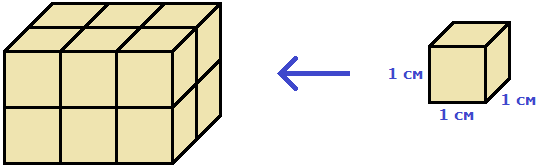
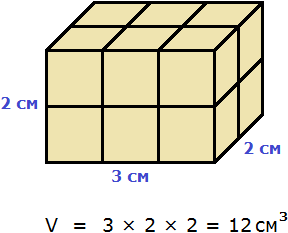
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см 3 ). Тогда объём V рассмотренного нами параллелепипеда равен 12 см 3
V = 12 см 3
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
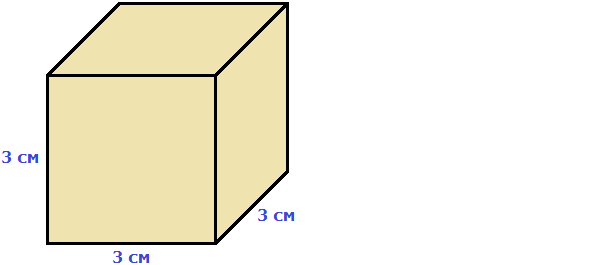
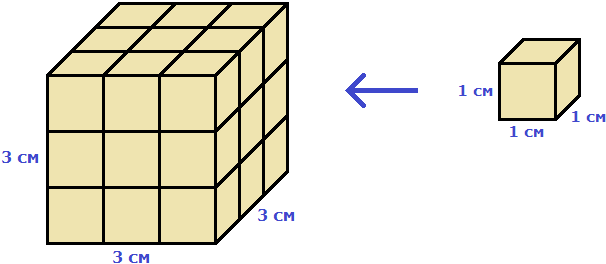
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
Таким образом, объём куба вычисляется по следующему правилу:
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах ( м 3 ). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах ( дм 3 ).
Другое название одного кубического дециметра – один литр.
1 дм 3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
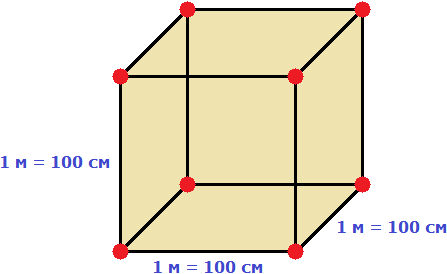
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 100 3 = 1 000 000 см 3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м 3 = 1 000 000 см 3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
Например, переведём 300 000 000 см 3 в кубические метры. Рассуждать в этом случае можно так: « если 1 000 000 см 3 это один кубический метр, то сколько раз 300 000 000 см 3 будут содержать по 1 000 000 см 3 »
300 000 000 см 3 : 1 000 000 см 3 = 300 м 3
Пример 2. Выразить 3 м 3 в кубических сантиметрах.
Умножим 3 м 3 на 1 000 000
3 м 3 × 1 000 000 = 3 000 000 см 3
Пример 3. Выразить 60 000 000 см 3 в кубических метрах.
60 000 000 см 3 : 1 000 000 см 3 = 60 м 3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм 3
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм 3
Теперь переведём эти 6000 дм 3 в кубические метры.
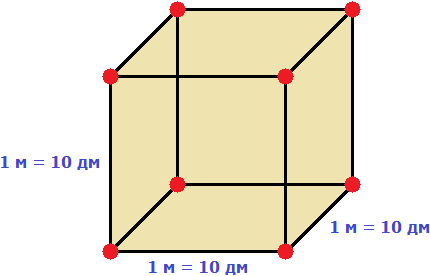
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1 000 дм 3
V = 10 3 = 1000 дм 3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм 3 содержит по 1 000 дм 3
6 000 дм 3 : 1 000 дм 3 = 6 м 3
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
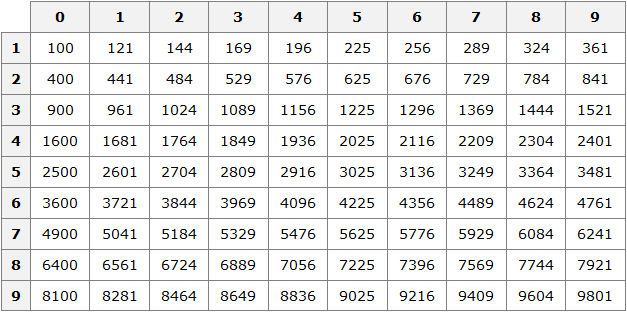
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
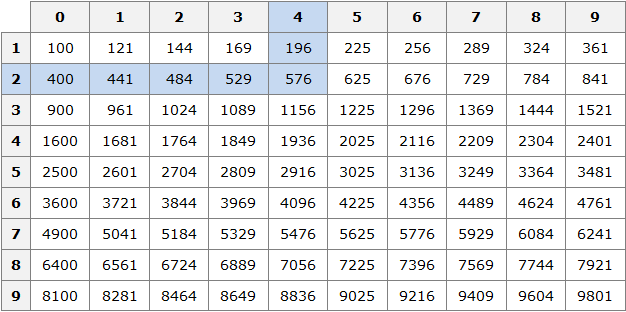
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
24 2 = 576
Таблица кубов
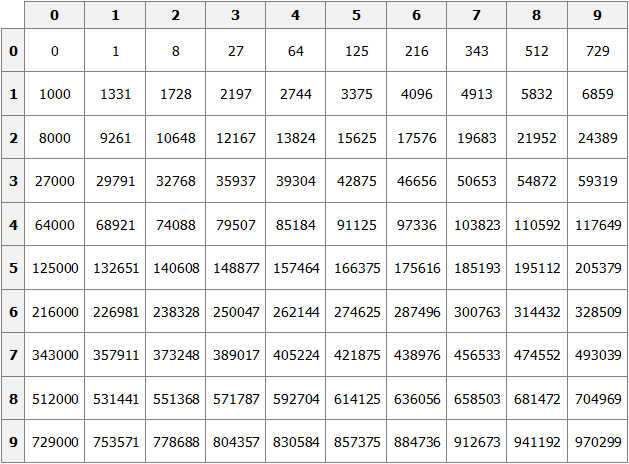
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
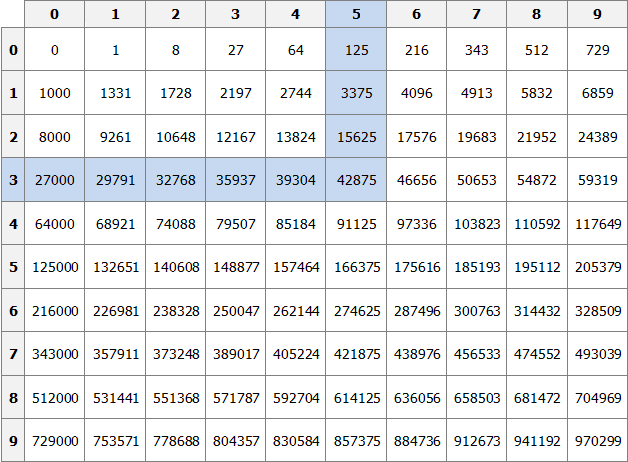
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
35 3 = 42875
Задания для самостоятельного решения
Решение
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Решение
Решение
Ответ: ширина прямоугольника составляет 2 см.
Решение
S = a 2
a = 8
S = 8 2 = 64 см 2
Ответ: площадь квадрата со стороной 8 см равна 64 см 2
Решение
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см 3
Решение
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
Ответ: пшеницей засеяно 12 га.
Решение
a = 42 м
b =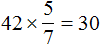 
м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м 3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм 3
35 525 л = 35 525 дм 3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм 3 : 1000 дм 3 = 35,525 м 3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
9 thoughts on “Периметр, площадь и объём”
Ура. Вы снова в деле. Всегда будем рады новым урокам.
Благодарю. Все четко, последовательно, без воды. Пожалуйста не останавливайтесь! Желаю успехов в ваших проектах.
Продовжуйте працювати! Спасибі, що ви випукаєте нові уроки. Чекаю на нові уроки із захопленням.
Продовжуйте працювати! Спасибі, що ви випукаєте нові уроки, я чекаю на них із захопленням.