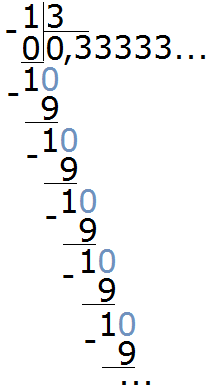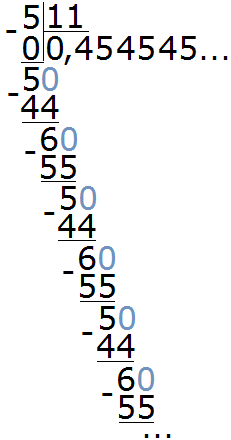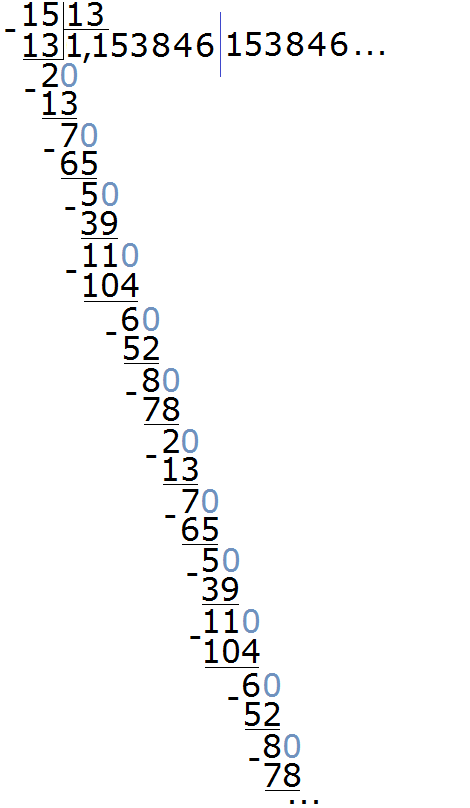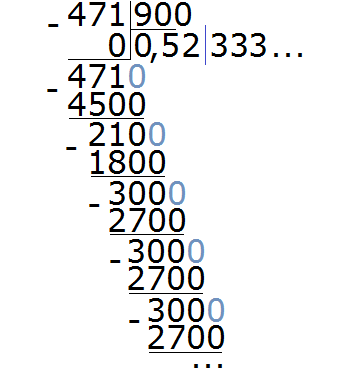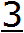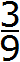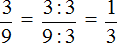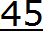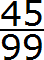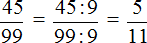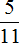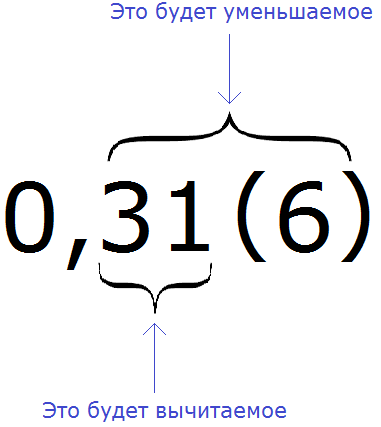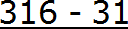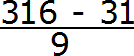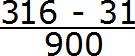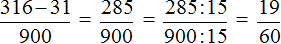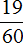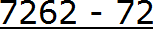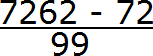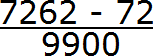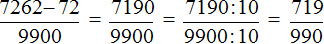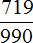ПЕРИОД
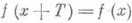
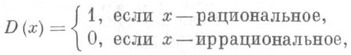
любое рациональное число 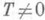
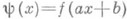
Аналогично определяется П. функции, определенной на нек-рой абелевой группе. А. А. Конюшков.
Полезное
Смотреть что такое «ПЕРИОД» в других словарях:
Период — (греч. periodos «обход», «окружность») термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или… … Литературная энциклопедия
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
Период — ПЕРИОД (Περιοδος обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состязания во время олимпийских празднеств. Этим термином Аристотель стал обозначать особый вид… … Словарь литературных терминов
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ПЕРИОД — муж. срок или промежуток времени, продолжительность; время от одного события до другого. История делится на периоды, сроки. Период первозданный период осадочный, сроки образованья земной толщи. | Длительность самого события, действия, состоянья;… … Толковый словарь Даля
ПЕРИОД — (1) промежуток времени, в течение которого начинается, развивается и заканчивается какой либо процесс; наименьший интервал времени, по истечении которого произвольно выбранные мгновенные значения периодической величины повторяются; (2) П. в… … Большая политехническая энциклопедия
Период С — Студийный а … Википедия
ПЕРИОД — срок протекания экономического процесса, действия, плана, договора, гарантии, уплаты долгов, внесения налогов, выполнения работ (гарантийный период, плановый период, период обложения, период окупаемости). Райзберг Б.А., Лозовский Л.Ш.,… … Экономический словарь
период — См … Словарь синонимов
ПЕРИОД — колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие период… … Современная энциклопедия
Периодические дроби
Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:
Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.
Получаем периодическую дробь
Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.
Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.
Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.
В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:
Читается как «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11
Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:
Читается как «ноль целых и сорок пять в периоде»
Пример 3. Разделить 15 на 13
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».
Пример 4. Разделить 471 на 900
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смéшанные.
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Избавляемся от хвоста
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.
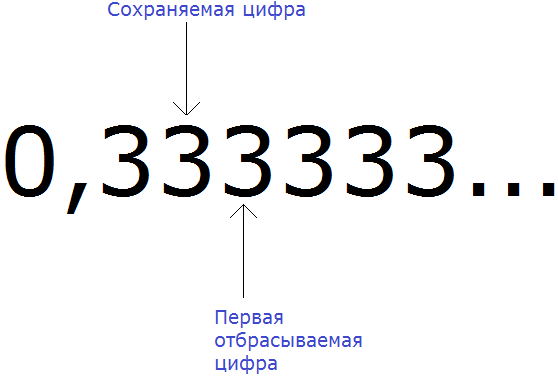
Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33
Округлим периодическую дробь 6,31 (6) до разряда тысячных.
Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317
Перевод чистой периодической дроби в обыкновенную дробь
Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.
Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.
Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.
Итак, записываем в числителе период дроби 0, (3) то есть тройку:
А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).
В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:
Полученную дробь 
Получили обыкновенную дробь 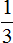
Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается
Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.
Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:
А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).
В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:
Полученную дробь 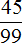
Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается
Перевод смешанной периодической дроби в обыкновенную дробь
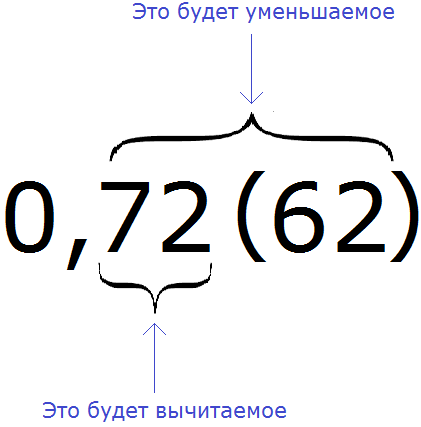
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)
В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)
В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
34 thoughts on “Периодические дроби”
Когда же следующие уроки? Уже что-то долго ничего нету
Большое спасибо за урок! Откровенно говоря…эту тему не помню вообще…Будто ее и не было в школе О__о Ну или я ее проболела… (Перевод смешанной периодической дроби в обыкновенную дробь)
Вы бы хоть номер кошелька написали. А то столько трудились и никакой отдачи. С такими уроками никакой экзамен не страшен.
Спасибо большое Тэла, за столь добрый отзыв ?
Если люди получают пользу от этих уроков — это уже отдача)
Огромное Вам спасибо за уроки! Всё объясняете доступно и наглядно! На ваших уроках готовлюсь поступать на ФИТ на программиста. Хорошо бы еще алгебру выложили.)
Вы не могли бы объяснить логику алгоритма перевода периодической дроби в обычную?
Зачем в знаменателе ставятся девятки — заместно, например, округления числа, подставляемого в числитель, до последней цифры периода, и постановки степени 10 в знаменатель? Зачем, при переводе смешанной периодической дроби, производится соотв. вычитание и чем объясняется подстановка нулей и единиц в зависимости от принадлежности цифры к периоду??…
Спасибо большое за урок ? Скажите пожалуйсто при округлении(когда избавляемся от хвоста) откуда знать до каких разряд надо округлять?
Вот и здесь последняя задача говорит округлить до разряда сотых,а почему не до десятых(например)?
зависит от задачи, которую решаете. Если в задаче сказано округлять до десятых, значит округляете до десятых. Если сказано округлять до сотых — округляете до сотых
период
Его стихи, романы и автобиографические книги повествуют о разных периодах его карьеры искателя приключений, авиатора, журналиста и поэта.
О минувших периодах истории мы судим по сохранившимся до наших дней памятникам культуры.
Период вращения этого спутника вокруг оси равен периоду его обращения вокруг Земли.
Полезное
Смотреть что такое «период» в других словарях:
Период — (греч. periodos «обход», «окружность») термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или… … Литературная энциклопедия
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
Период — ПЕРИОД (Περιοδος обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состязания во время олимпийских празднеств. Этим термином Аристотель стал обозначать особый вид… … Словарь литературных терминов
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ПЕРИОД — муж. срок или промежуток времени, продолжительность; время от одного события до другого. История делится на периоды, сроки. Период первозданный период осадочный, сроки образованья земной толщи. | Длительность самого события, действия, состоянья;… … Толковый словарь Даля
ПЕРИОД — (1) промежуток времени, в течение которого начинается, развивается и заканчивается какой либо процесс; наименьший интервал времени, по истечении которого произвольно выбранные мгновенные значения периодической величины повторяются; (2) П. в… … Большая политехническая энциклопедия
Период С — Студийный а … Википедия
ПЕРИОД — срок протекания экономического процесса, действия, плана, договора, гарантии, уплаты долгов, внесения налогов, выполнения работ (гарантийный период, плановый период, период обложения, период окупаемости). Райзберг Б.А., Лозовский Л.Ш.,… … Экономический словарь
период — См … Словарь синонимов
ПЕРИОД — колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие период… … Современная энциклопедия
Значение слова «период»
2. Спец. Промежуток времени, в течение которого заканчивается какой-л. повторяющийся процесс. Период колебания.
3. Геол. Промежуток времени, в течение которого образовались горные породы определенной геологической системы отложений; часть эры, делящаяся в свою очередь на эпохи. Каменноугольный период палеозойской эры.
4. Мат. Группа повторяющихся цифр в бесконечной десятичной дроби.
5. Грамм. Сложное синтаксическое целое, состоящее из одного сложного предложения или из соединения нескольких предложений, части которого связаны между собой грамматически, лексически и интонационно.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
В физике, астрономии:
Период колебаний — время (в секундах) между двумя последовательными прохождениями тела через одно и то же положение в одном и том же направлении, величина, обратная частоте.
Период полураспада — время, за которое число ядер данного изотопа уменьшается в два раза.
Период периодической системы — строка периодической таблицы, объединяющая элементы с одинаковым числом электронных оболочек.
В хронологии (истории, археологии, палеонтологии) — единица хронологической классификации: выделенный в прошлом промежуток времени связанный с некими событиями или обладающий некими характерными особенностями.
Период (риторика) — пространное предложение, отличающееся полнотой развёртывания мысли и законченностью интонации.
В хоккее с шайбой или пляжном футболе — одна из трёх частей матча.
ПЕРИ’ОД, а, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к-рого заканчивается какой-н. повторяющийся процесс (науч.). Синодический п. обращения планеты (время, в течение к-рого планета совершает один полный оборот вокруг Солнца; астр.). П. колебательного движения (время, в течение которого тело возвращается в исходное положение; физ.). 2. Промежуток времени, противопоставляемый другим, определенный срок, в течение к-рого что-н. происходило, произошло. Одесский п. жизни Пушкина. В течение долгого периода был учителем. В п. подготовки чего-н. || Промежуток времени, характеризующийся тем или иным социально-политическим, культурно-историческим явлением, отдельная часть какого-н. исторического процесса. . Мы имеем теперь последний период НЭП<>‘а, конец НЭП’а, период полной ликвидации капитализма во всех сферах народного хозяйства. Сталин (доклад на Чрезвычайном VIII Всесоюзном съезде советов 25/XI 1936 г.). П. военного коммунизма. П. нэпа. Реконструктивный п. Классический п. русской литературы. 3. Часть эры, делящаяся в свою очередь на эпохи (геол.). Пермский п. палеозойской эры. Верхняя эпоха мелового периода мезозойской эры.
4. Промежуток времени, в течение которого заканчивается какой-н. процесс (науч.). Инкубационный п. болезни. 5. Величина, выражающая промежуток, через который повторяется значение функции (мат.). 6. Группа повторяющихся цифр в бесконечной десятичной дроби (мат.). 7. Сложное синтаксическое построение для подробного развития мысли (предложение, распространенное многими второстепенными членами или многими придаточными предложениями, или же соединение многих равносильных предложений), употребляемое как стилистический прием с целью благозвучия, к-рое достигается ритмическим расположением частей, повышением и понижением голоса (лит.). Простой п. (с одним главным предложением). Сложный п. (со многими главными предложениями). || Неточно — вообще длинное синтаксическое целое, длинная фраза из многих предложений и т. п. (разг.). Пишите короче, избегайте периодов.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
пери́од
1. отрезок времени, в течение которого циклический процесс совершает полный цикл изменений ◆ Ряд явлений на Земле повторяется с периодом вращения Солнца (около 27 дней). ◆ Цикл измерений повторяется с периодом 1 сек.
2. отрезок времени как этап, стадия какого-либо процесса ◆ Послевоенное время стало для неё периодом небывалого успеха. ◆ Принято считать, что в советский период русская философия не имела никаких перспектив для своего развития. ◆ Был у меня период в жизни, когда я подсел на кофе, почти как наркоман.
3. спорт. отдельная, изолированная часть матча в хоккее и некоторых других командных играх ◆ Первый период наша команда имела преимущество; во втором периоде было очень много удалений; что в свою очередь поломало игру, третий период нащи хоккеисты играли строго в обороне, старались не позволить сопернику выходить на активные зоны.
4. матем. ненулевая величина (обычно наименьшая положительная), прибавление которой к аргументу периодической функции не изменяет значений этой функции ◆ Хорошим примером периодических функций могут служить тригонометрические функции y = sin x, y = cos x (период этих функций равен 2π).
5. матем. бесконечно повторяющаяся последовательность цифр после запятой в позиционной записи рационального числа ◆ При делении в столбик 1 на 7 встретятся все остатки от 1 до 6, а в периоде будет шестизначное число 142857.
6. устар. лингв. то же, что предложение ◆ Точка заключает целый период, и ей обыкновенно следует прописная буква, которою также имена почтенные и собственные начинаются. М. В. Ломоносов, «Российская грамматика», 1755 г. (цитата из НКРЯ)
7. геол. промежуток времени, в течение которого отложился слой пород, образующих соответствующую геологическую систему ◆ Еще в юрский период в Центральной Азии были многочисленные озера и на их берегах пышная растительность, судя по присутствию пластов угля в юрских толщах. В. А. Обручев, «В дебрях Центральной Азии», 1951 г. (цитата из НКРЯ)