Интервал (математика)
Термин промежуток используется в составе сложных терминов:
Кстати, в английском языке словом interval называется отрезок. А для обозначения понятия интервала используется термин open interval.
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Интервал (математика)» в других словарях:
Промежуток (математика) — Промежуток, или более точно, промежуток числовой прямой множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними[1]. С использованием логических символов, это определение… … Википедия
Портал:Математика — Начинающим · Сообщество · Порталы · Награды · Проекты · Запросы · Оценивание География · История · Общество · Персоналии · Религия · Спорт · Техника · Наука · Искусство · Философия … Википедия
Регрессия (математика) — У этого термина существуют и другие значения, см. регрессия. Регрессия (лат. regressio обратное движение, отход), в теории вероятностей и математической статистике, зависимость среднего значения какой либо величины от некоторой другой… … Википедия
Промежутки (математика) — Промежуток, открытый промежуток, интервал множество точек числовой прямой, заключённых между двумя данными числами a и b, то есть множество чисел x, удовлетворяющих условию: a Википедия
Апории Зенона — … Википедия
Средняя — периодическое увлажнение пола, при котором поверхность покрытия пола влажная или мокрая; покрытие пола пропитывается жидкостями. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением м … Словарь-справочник терминов нормативно-технической документации
«Новая хронология» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
Критика естественно-научных методов в «Новой хронологии» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
Критика естественно-научных методов в «Новой хронологии» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
Новая Хронология — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
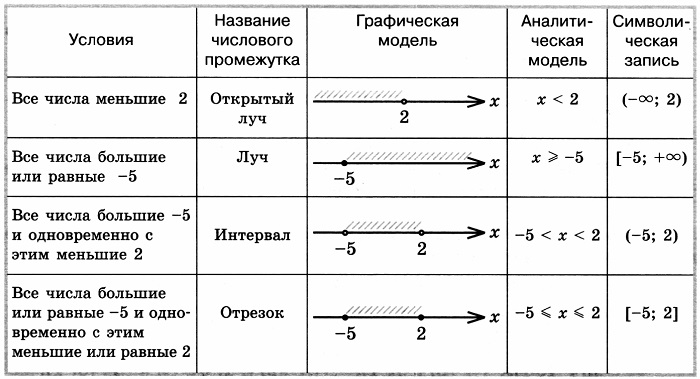
Таблица числовых промежутков: виды, обозначения, изображения
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x a включает в себя точки, которые расположены левее, а для x > a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.
Рассмотрим несколько примеров.
Для наглядного примера зададим числовой луч.
Рассмотрим рисунок, приведенный ниже.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.
Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.
Виды числовых промежутков
На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.
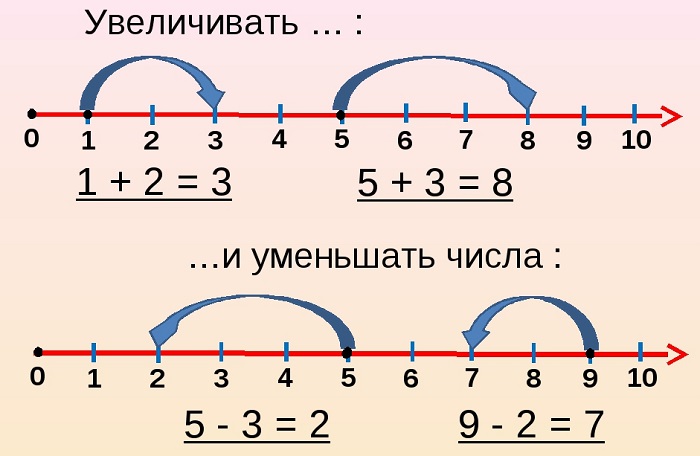
Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.
На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.
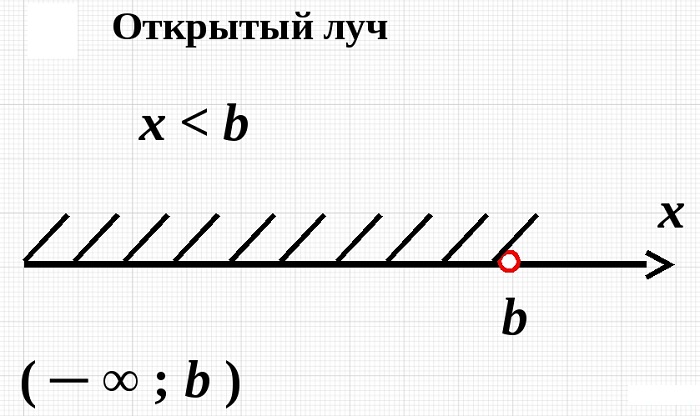
Открытый числовой луч
Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.
Точки расположены по одну сторону от определенной переменной, признанной началом координат.
Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:
Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».
Также можно охарактеризовать неравенством:
Знак зависит от расположения луча относительно А.
Замкнутый числовой луч
Замкнутый луч отличается от открытого тем, что к множеству относится А.
Также ему соответствует условие:
х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
х ≥ А (значение больше или равно А) или [А; +∞).
При графическом изображении А в этом случае закрашивается, на рисунке она черная.
Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.
Числовой отрезок
Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.
При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.
Интервал
Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.
Числовые промежутки. Контекст. Определение
Введём понятие числового промежутка. Среди числовых множеств, то есть множеств, объектами которых являются числа, выделяют так называемые числовые промежутки. Их ценность в том, что очень легко вообразить множество, соответствующее указанному числовому промежутку, и наоборот. Поэтому с их помощью удобно записывать множество решений неравенства. Тогда как множеством решения уравнения будет не числовой промежуток, а просто несколько чисел на числовой прямой, с неравенствами, иначе говоря, любыми ограничениями значения переменной появляются числовые промежутки.
— это множество всех точек числовой прямой, ограниченное данным числом или числами (точками на числовой прямой).
Числовой промежуток любого вида (множество значений x, заключённых между некоторыми числами) всегда можно представить тремя видами математических обозначений: специальными обозначениями промежутков, цепочками неравенств (одним неравенством или двойным неравенством) или геометрически на числовой прямой. По сути, все эти обозначения имеют один смысл. Они дают ограничение(-я) для значений какого-то математического объекта, переменной величины (некоторой переменной, любого выражения с переменной, функции и т.д.).
Из вышесказанного можно понять, что так как можно по-разному ограничить область числовой прямой (есть разные типы неравенств), то и типы числовых промежутков бывают разные.
Виды числовых промежутков
Каждый тип числового промежутка имеет собственное название, особое обозначение. Для обозначения числовых промежутков используют круглую и квадратную скобку. Круглая скобка означает, что конечная, определяющая границу, точка на числовой прямой (конец) у этой скобки не входит во множество точек данного промежутка. Квадратная скобка означает, что конец входит в промежуток. С бесконечностью (с этой стороны промежуток не ограничен) используют круглую скобку. Иногда вместо круглых скобок можно писать квадратные, повёрнутые в обратную сторону: (a;b) ⇔]a;b[
С помощью промежутков в математике обозначается очень большое количество вещей: есть промежутки изоляции при решении уравнений, промежутки интегрирования, промежутки сходимости рядов. Промежутками принято всегда обозначать при при исследовании функции её область значений и область определения. Промежутки очень важны, например, есть теорема Больцано — Коши (можно узнать больше в «Википедии»).
Системы и совокупности неравенств
Система неравенств
Любую систему можно решать графически с использованием числовой прямой. Там, где решения составляющих систему неравенств пересекаются и будет решение самой системы.
Представим для каждого случая графическое решение.
Далее, системы неравенств можно классифицировать как равносильные, если они имеют общее множество решений. Отсюда (как можно видеть выше) следует, что более сложные системы можно упрощать (например, используя геометрическое решение).
Фигурную скобку можно условно, грубо говоря, назвать эквивалентом союза «И» для неравенств
Совокупность неравенств
Итак, все неравенства в совокупности объединяют скобкой совокупности «[«. Если значение переменной удовлетворяет хотя бы одному неравенству из совокупности, то оно принадлежит множеству решений всей совокупности. Также и с уравнениями (опять же их можно назвать частным случаем).
Метод интервалов, решение неравенств
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
Квадратное неравенство можно решить двумя способами:
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком