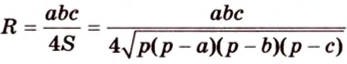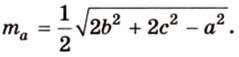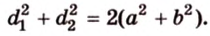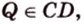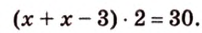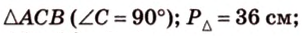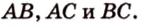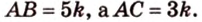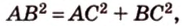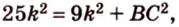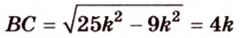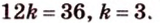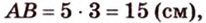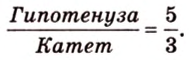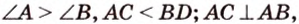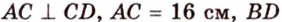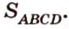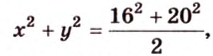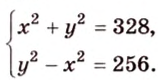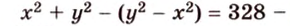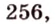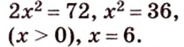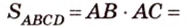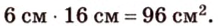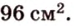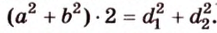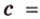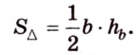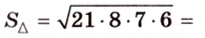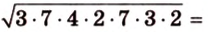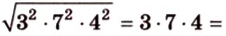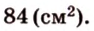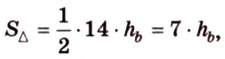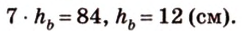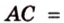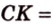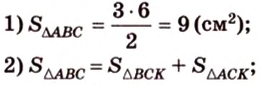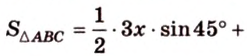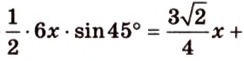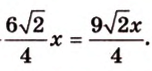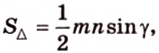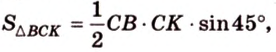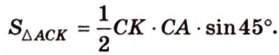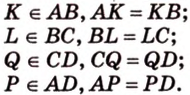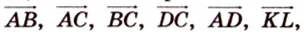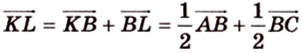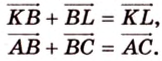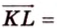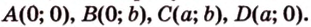Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Как набрать символ «пусть»?
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
Похоже, но хотелось бы, чтобы он с кванторами одного размера был. А этот довольно сильно отличается: 
Нашёл на просторах такую самоделку
Схожая проблема. Пользуюсь XeLaTeX и LuaLaTeX с unicode-math. Проблема в том, что в стандарт Unicode не включён этот значок «пусть», соответственно, его нет ни в шрифтах, ни в TeXе.
Я надумал подать в Unicode Consortium заявку на включение символа. Для этого нужны ссылки на авторитетные источники (публикации, книги), которые бы объясняли смысл значка/использовали его. Никто не поделится такими? Мой единственный источник — лектор по матанализу, но лекции к заявке не пришьёшь. Больше нигде не встречал, кроме как здесь.
| Заслуженный участник |
Удивительно! Преподаватель не знает квантора «пусть»! Да ещё и удивляется, где он нужен! Видимо, в заборостроительном институте теорем не доказывают.
| Админ форума |
| Заблокирован |
Последний раз редактировалось exitone 09.01.2014, 10:34, всего редактировалось 8 раз(а).
По-вашему, кванторы необходимы для доказательства теорем? Мне всегда казалось, что они для удобства.
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
Последний раз редактировалось Maslov 27.01.2014, 15:19, всего редактировалось 1 раз.
Конспектировать приходилось очень много, поэтому даже такие простые сокращения были полезны.
Без него вполне можно обойтись, поэтому использовать эту закорючку никого не призываю. Просто спросил.
PS. Естественно, это никакой не квантор.

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Изучаем символы: как обозначается в математике площадь
В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе. В этом заведении ученик получает базовые знания и навыки. В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
Общие сведения

Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.
Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.
В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.

Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.
Важно! Основы геометрии: что это такое биссектриса треугольника
Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:

Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект.
Познавательно! Как найти и чему будет равна длина окружности
Общее понимание категории позволяет ее трактовать в качестве числовой характеристики. При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.
Важно! Урок геометрии: как найти по формуле периметр треугольника
Варианты обозначения

В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.
В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину.
В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение <эс>.
Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.

Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.
Интересно! Что значит вертикально и как выглядит вертикальная линия
Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.
Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
Полезное видео
Подведем итоги
Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.
Геометрические термины на английском языке
В повседневной жизни мы постоянно используем слова, связанные с геометрией. Я имею в виду не термины вроде гипотенуза или биссектриса, а употребительные слова, например: круг, квадратный, длина, ширина, объем. Из этой подборки вы узнаете самые необходимые геометрические термины на английском языке и сможете повторить или выучить их с помощью озвученных карточек.
Содержание:
Основные геометрические термины на английском языке
Пройдите тест на уровень английского:
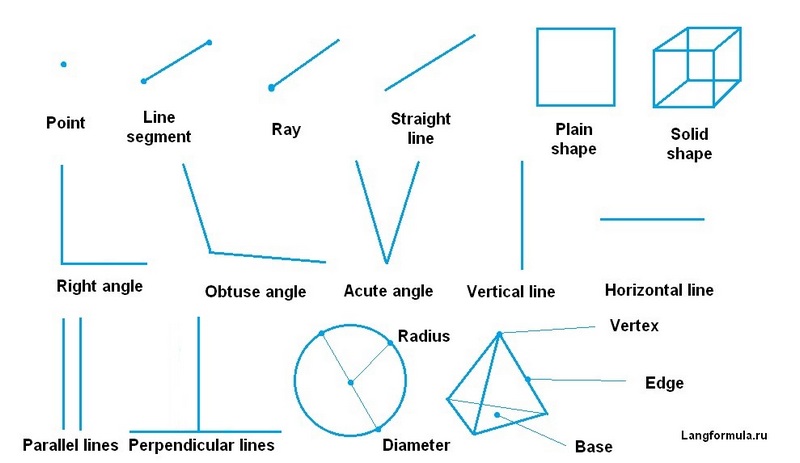
Когда я учился в школе, мы начинали знакомство с геометрией с таких элементарных понятий, как точка (point), прямая (straight line), отрезок (line segment), луч (ray), затем перешли к геометрическим фигурам (plane shapes) и геометрическим телам (solid shapes).
В списке и карточках ниже представлены эти и другие основные термины. Отмечу, что наиболее коварными являются два термина:
- Angle – угол. Легко перепутать с corner. Но если corner – это угол в общем смысле, например, угол комнаты (corner of the room), то angle – это угол как геометрическое понятие (right angle — прямой угол). Point – точка. В русском языке любая точка называется точкой: будто то точка в десятичной дроби или конце предложения. В английском несколько названий для разных точек: point, dot, period, full stop. Вот какая между ними разница:
- Point – точка в геометрии, в десятичных дробях: 3.14 читается как three point one four. Dot – точка в адресах веб-сайтов. Например, www.google.com читается как: double u double u double u google dot com. Кстати, забавно, что www – это сокращенно world wide web, но сокращенная форма при чтении намного длиннее полной. Period (США) или full stop (Великобр.) – точка в конце предложения. Есть даже английское выражение “period” или “full stop” аналог русского «точка» в значении «разговор закончен, возражения не принимаются»: You are not going to the party. Period. – Ты не идешь на вечеринку. Точка.
| point | точка |
| line segment | отрезок |
| ray | луч |
| line | прямая |
| plane shape | геометрическая фигура |
| solid shape | геометрическое тело |
| volume | объем |
| area | площадь |
| perimeter | периметр |
| diagonal | диагональ |
| size | размер |
| side | сторона |
| angle | угол |
| lengh | длина |
| width | ширина |
| height | высота |
| depths | глубина |
| right angle | прямой угол |
| obtuse angle | тупой угол |
| acute angle | острый угол |
| vertical line | вертикальная линия |
| horizontal line | горизонтальная линия |
| curved line | кривая линия |
| broken line | ломаная линия |
| parallel lines | параллельные линии |
| perpendicular lines | перпендикулярные линии |
| radius | радиус |
| diameter | диаметр |
| base | основание |
| vertex | вершина |
| edge | ребро |
| convex | выпуклый |
| concave | вогнутый |
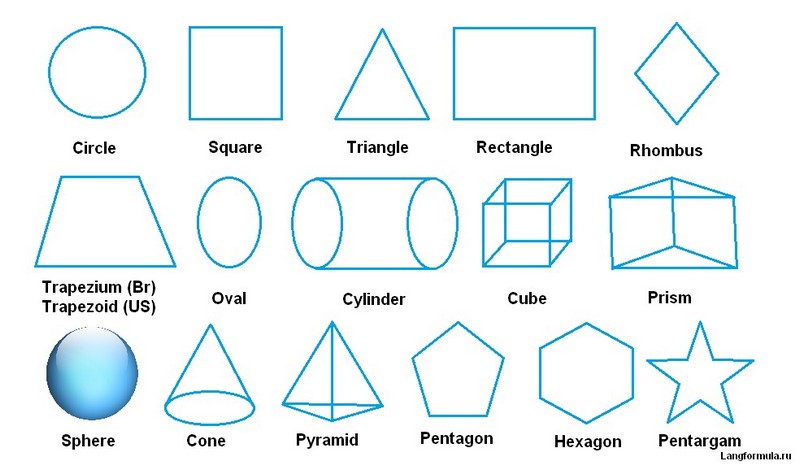
Геометрические тела и фигуры
Напомню, геометрические фигуры двухмерные, а тела – объемные. Квадрат, треугольник – это фигуры, а куб, пирамида – тела. Некоторые трудности могут возникнуть с прилагательными, образованными от названий тел и фигур, потому что они образуются по-разному:
- с помощью суффиксов: rectangle (прямоугольник) – rectangular (прямоугольный). обозначаются другим словом: circle (круг) – round (круглый). образуются без изменения слова: oval (овал) – oval (овальный).
От слова circle также образуется прилагательное circular – круглый, но оно обычно используется, когда речь идет о чем-то плоском и, как правило, идеально круглом. Round может применяться к плоским и объемным предметам, это слово намного употребительнее в повседневной речи: round table – круглый стол, round building – круглое здание. О шаровидных предметах тоже, скорее всего скажут, что они round (round ball – круглый мяч), хотя технически они spherical. Но по-русски мы тоже не называем мяч «сферическим».
Содержание:
Что такое планиметрия
Логическое построение планиметрии можно описать как последовательность следующих этапов.
Для школьного курса планиметрии определены:
К определяемым понятиям в геометрии относят отрезок, луч, треугольник и т. п., поскольку для них существуют объяснения «что это такое?». Определяемых понятий много. Приведем пример.
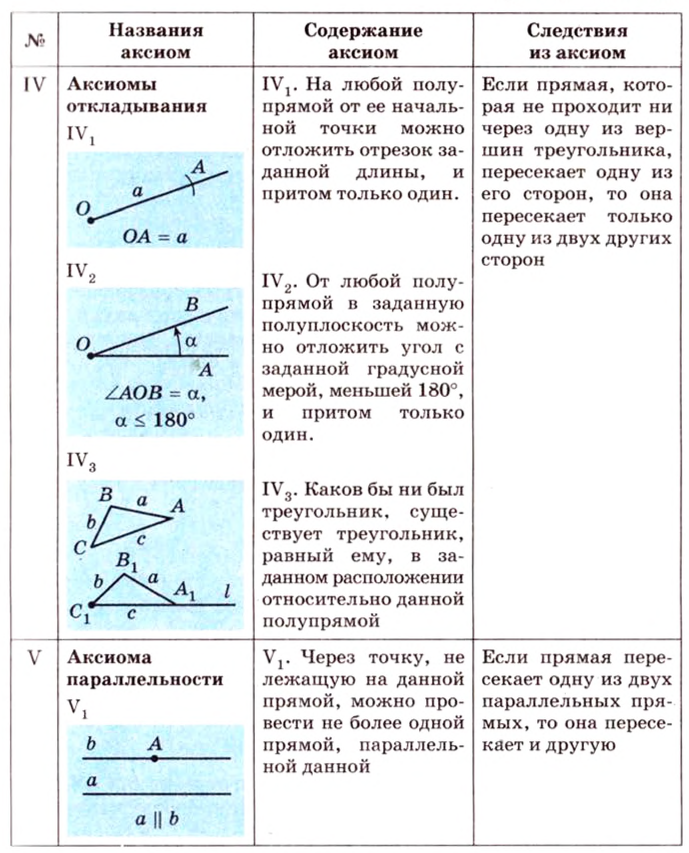
Аксиомы планиметрии
С целью установления правильности утверждения о свойствах той или иной геометрической фигуры прибегают к некоторым рассуждениям. Среди них есть такие, которые требуют доказательства (теоремы, задачи). Утверждение, истинность которого устанавливается путем доказательства и которое используется для доказательства других утверждений, называют теоремой.
Теорема состоит из: условия и вывода. Для доказательства теорем в школьном курсе геометрии в основном используют следующие методы:
Все рассуждения при доказательстве теорем произвольным методом основываются на аксиомах и известных доказанных фактах. Т.е. чтобы доказать теорему, разрешается пользоваться только основными свойствами простейших фигур (аксиомами) и свойствами, доказанными ранее (теоремами). Никакими другими свойствами фигур, даже если они представляются очевидными, пользоваться нельзя. Например, доказывая теоремы, можно использовать рисунки. Однако это лишь геометрическая модель содержания текста, выраженного словами, поэтому делать по рисунку выводы о свойствах фигур не разрешается.
Итак, геометрия, как и другие математические науки, строится по такой схеме: сначала следует ввести основные понятия, задать аксиомы (правила игры), а потом, опираясь на аксиомы, выводить другие факты (проводить игру по определенным правилам, не противоречащим друг другу).
Опорные факты курса планиметрии
Данный параграф предназначен для повторения курса планиметрии. Необходимость в нем обусловлена тем, что многие вопросы планиметрии на первом этапе обучения в школе рассматриваются несколько поверхностно. В следующих классах уровень изучения материала повышается, а вернуться и углубить пройденное удается не всегда. Поэтому мы систематизируем и обобщим основные сведения по планиметрии, условно разбив их на блоки: взаимное расположение прямых на плоскости; окружность и круг; многоугольники; треугольник и его элементы; выпуклые четырехугольники.
Взаимное расположение прямых на плоскости
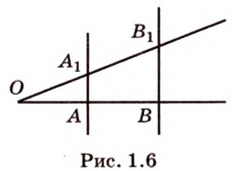
Расстоянием от точки 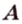
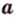
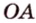
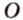
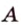
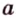
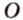
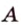
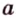
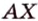
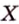
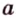
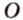
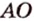
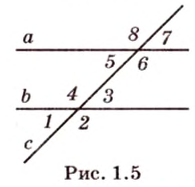
Две различные прямые 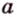
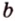
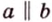
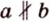
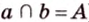
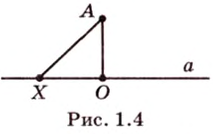
Вследствие пересечения двух прямых третьей прямой образуется восемь углов (рис. 1.5) (прямые а и Ь могут пересекаться, но прямая с через точку их пересечения не проходит):
Признаки параллельности прямых:
Окружность и круг
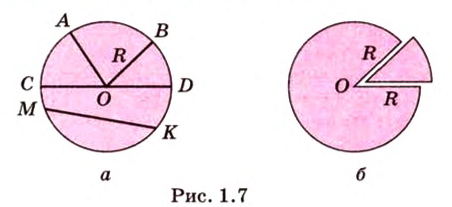
Кругом с центром 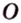
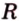
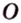
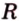
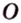
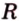
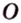
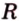
Отрезки, которые соединяют центр с точками окружности и имеют длину 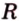
Части круга, на которые он делится двумя радиусами, называют круговыми секторами (рис. 1.7, б).
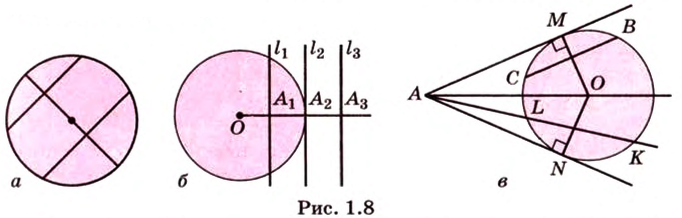
Через три точки, не лежащие на одной прямой, проходит единственная окружность. Диаметр, перпендикулярный к хорде, делит пополам эту хорду и обе дуги, которые стягиваются ею, и наоборот, если диаметр проведен через середину хорды, то он перпендикулярен этой хорде и делит пополам дугу, которую она стягивает (рис. 1.8, а).
Дуги, которые находятся между параллельными хордами, равны между собой. Равные дуги стягиваются равными хордами, и наоборот, равные хорды стягивают равные дуги.
Равные хорды одинаково отдалены от центра, и наоборот, хорды, одинаково отдаленные от центра, равны между собой. Большая из двух хорд меньше отдалена от центра, и наоборот, из двух хорд больше та, которая меньше отдалена от центра (рис. 1.8, а).
Каким может быть взаимное расположение прямой и окружности?
Рассмотрим окружность с центром 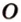
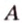
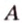
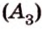
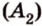
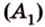
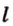
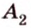
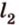
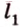
Прямая, проходящая через точку окружности, является касательной к окружности только тогда, когда она перпендикулярна радиусу, проведенному в эту точку. Если касательная параллельна хорде окружности, то точка касания делит пополам дугу, которую стягивает хорда (рис. 1.8, в; 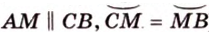
Если из одной точки к окружности проведены две касательные, то отрезки этих касательных (от точек касания до данной точки) равны между собой, а луч, проведенный через данную точку и центр окружности, делит пополам угол между касательными (рис. 1.8, в; 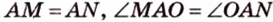
Угол, образованный двумя касательными, называется описанным (рис. 1.8, в; 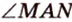
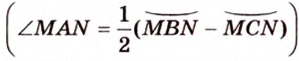
Многоугольники
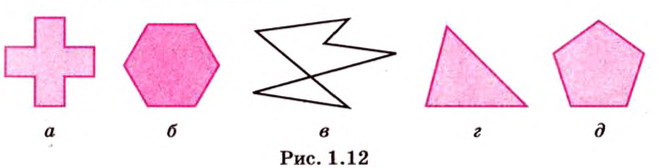
Многоугольник выпуклый, если он лежит в одной полуплоскости относительно каждой прямой, проходящей через две его соседние вершины (рис. 1.12, б, г, д).
Многоугольники называют равными, если при наложении они совмещаются. Для выпуклого 
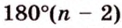

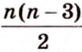

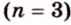
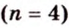
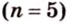
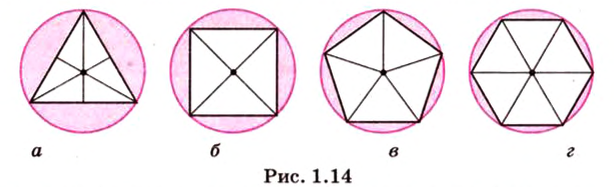
Как построить правильный 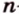
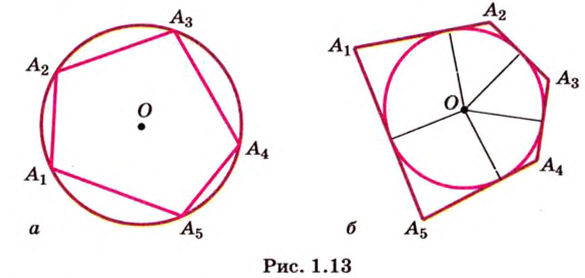
Если окружность разделить на 

Если окружность разделить на 

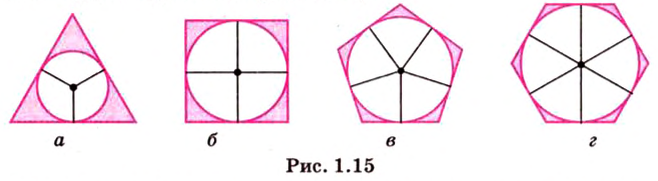
Вокруг каждого правильного многоугольника можно описать окружность или в каждый правильный многоугольник можно вписать окружность.
В правильном многоугольнике центры описанной и вписанной окружностей совпадают. Общий центр описанной и вписанной окружностей называется центром правильного многоугольника. Радиус вписанной окружности называют апофемой правильного многоугольника.
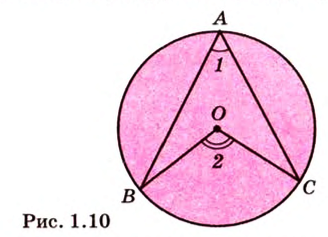
Угол, образованный двумя радиусами, проведенными через смежные вершины правильного многоугольника, называется его центральным углом. Все центральные углы правильного многоугольника равны между собой и составляют 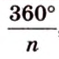

В правильном 

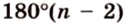
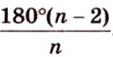
Окружность, вписанная в правильный многоугольник, касается его сторон в их серединах. Центр окружности, вписанной в правильный многоугольник, является точкой пересечения серединных перпендикуляров его сторон (рис. 1.15).
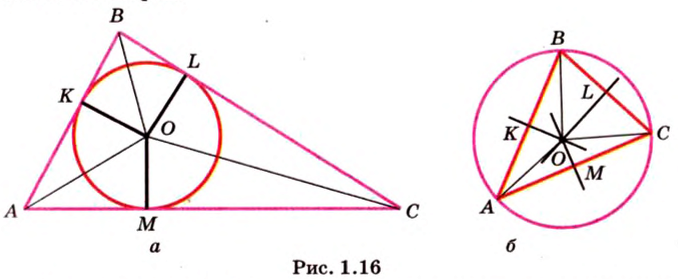
Простейшим многоугольником является треугольник. В любой треугольник можно вписать окружность, причем только одну. На рисунке 1.16, 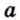
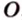

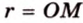
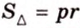
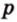
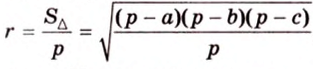
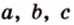
Можно ли в любой четырехугольник вписать окружность?
Ответ. Нельзя. В четырехугольник можно вписать окружность только при условии, что суммы длин его противоположных сторон равны.
Вокруг произвольного треугольника можно описать окружность, притом только одну (см. рис. 1.16, б). Центр окружности, описанной вокруг треугольника, является точкой пересечения серединных перпендикуляров, проведенных к его сторонам. Центр окружности 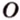
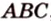
На рисунке 1.16, б изображена окружность с центром 
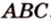
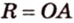
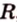
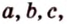
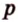
Можно ли описать окружность вокруг произвольного четырехугольника?
Ответ. Нельзя. Вокруг четырехугольника можно описать окружность только тогда, когда суммы противоположных углов равны 180°.
Треугольник и его элементы
Треугольником называется фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки. Рассмотрим 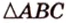
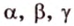
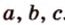
Треугольник называется тупоугольным, прямоугольным или остроугольным, если его наибольший внутренний угол соответственно больше, равен или меньше 90°.
Треугольник называется равнобедренным, если у него две стороны равны (боковые стороны). Основанием равнобедренного треугольника является сторона, которая не равна ни одной из двух других равных сторон.
Треугольник, все стороны которого равны, называется равносторонним, или правильным.
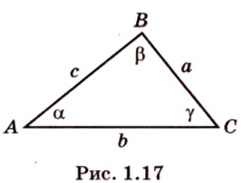
Соотношение между сторонами и углами треугольника:
Треугольник можно определить любой тройкой таких основных элементов: либо двумя сторонами и углом между ними, либо одной стороной и двумя углами, либо тремя сторонами.
Например, 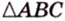
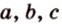
Соотношение между внутренними и внешними углами треугольника: любой внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Из трех отрезков можно образовать треугольник тогда и только тогда, когда любая его сторона меньше суммы и больше разности двух других его сторон. В любом треугольнике можно провести три медианы, три биссектрисы и три высоты.
Свойства биссектрисы угла треугольника: биссектрисы треугольника пересекаются в одной точке, которая лежит в середине треугольника и является центром вписанной
в него окружности.
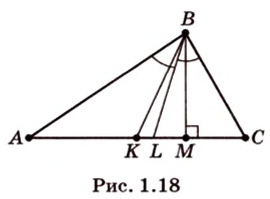
Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим к ней сторонам (рис. 1.18; 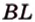
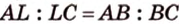
Основные свойства медиан треугольника:
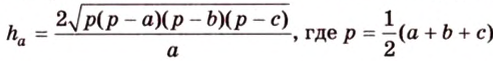
Медиана треугольника 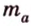
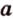
Свойства равнобедренного треугольника: углы при основании треугольника равны; высота, проведенная к основанию, является также биссектрисой и медианой.
Свойства равностороннего треугольника: все углы равны (каждый угол равен 60°); каждая из трех высот является также биссектрисой и медианой; центр окружности, описанной вокруг треугольника, совпадает с центром окружности, вписанной в него.
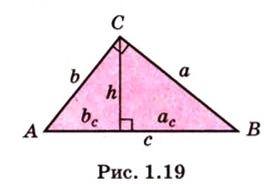
Стороны прямоугольного треугольника 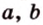
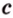
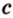
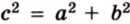
длины гипотенузы равен сумме квадратов длин катетов.
Свойства прямоугольного треугольника:
Выпуклые четырехугольники
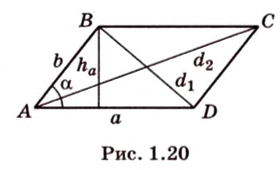
Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом (рис. 1.20).
Если в четырехугольнике исполняется любое из таких условий:
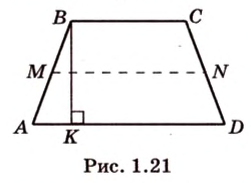
Если боковые стороны трапеции равны между собой, такую трапецию называют равнобокой (рис. 1.21; 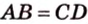
Равнобокая трапеция имеет такие свойства:
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией (рис. 1.21; 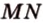
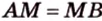
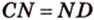
Средняя линия трапеции параллельна ее основаниям и равна их полусумме (рис. 1.21; 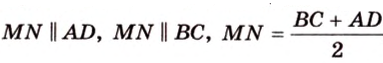
Задачи и методы их решения
Для геометрии закономерным является то, что введенные основные понятия и сформулированная аксиоматика составляют основу для новых утверждений. Однако справедливость последних необходимо доказывать путем определенных рассуждений, основывающихся на ранее доказанных утверждениях или аксиомах. Так формируются математические задачи.
Что такое математическая задача?
Можно ли утверждать, что для успешного решения геометрических задач и доказательства теорем достаточно свободно владеть всем теоретическим материалом?
Нет. Это не так. При хорошем знании теории следует овладеть еще и практическими навыками. А это возможно только в процессе решения задач, начиная с простейших и постепенно переходя к более сложным.
Математические задачи условно разделены на четыре вида, в соответствии с их требованиями: задачи на вычисление, доказательство, исследование и построение. С ними вы уже ознакомились в курсе планиметрии.
Приступая к решению задачи, следует выбрать метод. Методы делят:
Суть синтетического метода заключается в том, что, исходя из условия задачи или теоремы с использованием известных утверждений строится цепочка логических рассуждений, последнее из которых совпадает с требованием задачи. Приведем пример.
Пример №1
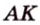
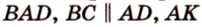
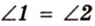
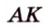
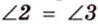
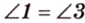
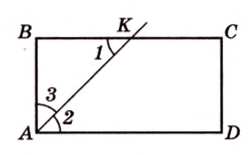
В 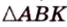
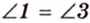
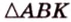
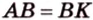
1. Если 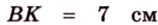
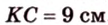
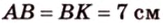
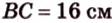
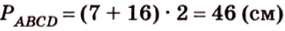
2. Если 
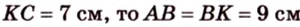
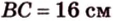
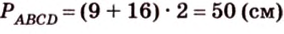
Ответ. 46 см или 50 см.
Эта задача является опорной, поскольку на такой идее строятся многие задачи и для параллелограмма, и для трапеции. У этих фигур биссектриса угла отсекает всегда равнобедренный треугольник.
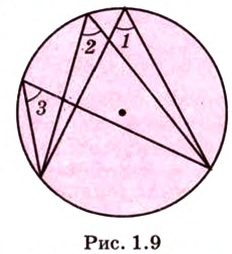
Отметим, что сокращенное обозначение углов в виде 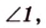
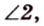
Как видим, в процессе решения задачи 1 используются только известные геометрические утверждения и производятся соответствующие вычисления. Причем для каждой геометрической задачи такие рассуждения свои.
Суть аналитического метода состоит в том, что, исходя из требования (вывода) утверждения (теоремы или задачи) и опираясь на известное утверждение, строится цепочка логических рассуждений, которая показывает, что требование является следствием условия. Приведем пример.
Пример №2
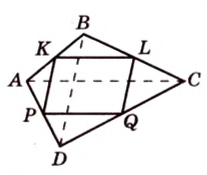
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 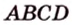

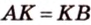
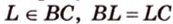

Доказать: 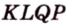
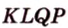
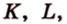
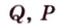
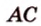
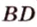
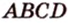
В 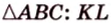
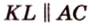
В 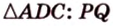

Имеем: 1. 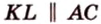
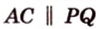
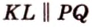
Чтобы решить задачу прямым методом, следует начать с анализа содержания задачи, от которого зависит выбор метода решения. Далее необходимо создать модель в виде рисунка и продолжить рассуждать над каждым действием, которые в совокупности образуют цепочку действий, ведущих либо от условия к требованию, либо от требования к условию.
Суть метода доказательства от противного состоит в том, что, имея утверждение, строим новое, возразив выводу данного. Формулируется утверждение. Исходя из вывода противоположного утверждения, строим цепочку истинных утверждений, пока не получим утверждение, которое противоречит либо условию, либо известной аксиоме или теореме, либо предположению. Таким образом приходим к выводу, что противоположное утверждение ошибочно, а потому исходное является истинным (тут действует логический закон: из двух противоположных утверждений одно истинное, другое ошибочное, третьего не дано). Рассмотрим пример.
Пример №3
Докажите утверждение: если две прямые параллельны третьей, то они параллельны между собой.
Строим противоположное утверждение: существуют две прямые, параллельные третьей и не параллельные между собой.
Математическую задачу считают решенной, если:
Метод от противного называют непрямым методом решения математических задач.
Рассмотрим некоторые другие методы решения геометрических задач, которые делят на виды по использованию математического аппарата.
Алгебраический метод решения задач
Решая задачу алгебраическим методом, следует уделить внимание таким этапам:
Приведем другие примеры решения задач алгебраическим методом.
Пример №4
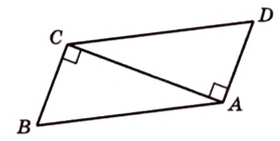
Периметр прямоугольного треугольника равен 36 см. Гипотенуза относится к катету как 5 : 3. Найдите стороны треугольника.
Дано: 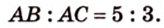
Найти:
Обозначим коэффициент пропорциональности через 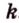
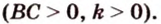
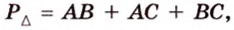
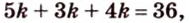
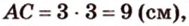
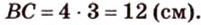
Ответ. 15 см, 9 см и 12 см.
Почему именно так?
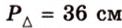
Пример №5
В параллелограмме диагонали равны 16 см и 20 см. Меньшая из них перпендикулярна к его стороне. Найдите площадь этого параллелограмма.
Дано: 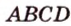
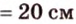
Найти:
Почему именно так?
Пусть 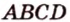
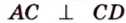
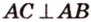
Обозначим стороны параллелограмма: 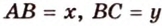
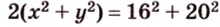
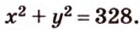
По теореме Пифагора из 
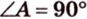
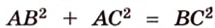
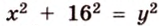
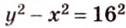
Составим систему уравнений:
Ответ.
В ходе решения этой задачи сначала выбираем формулу для вычисления площади параллелограмма. 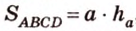
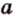
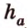
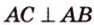
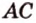
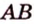
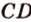
Метод площадей
Пример №6
Стороны треугольника равны 13 см, 14 см и 15 см. Вычислите высоту, проведенную к стороне, которая имеет длину 14 см.
Пусть 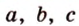
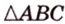
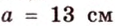
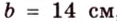
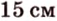
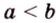
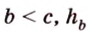
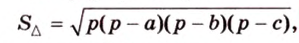
Ответ. 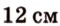
Имея три стороны треугольника 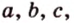
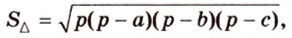
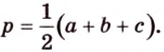
С другой стороны, площадь треугольника можно найти по формулам: 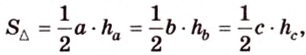
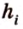

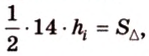
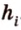
Отметим, что хотя во время решения задачи 6 использовалось алгебраическое уравнение, более существенными в решении этой задачи являются рассуждения о площади фигуры. Поэтому такой метод получил название метод площадей.
Пример №7
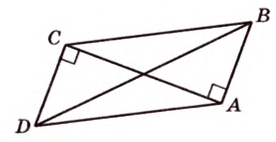
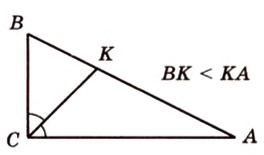
Катеты прямоугольного треугольника равны 3 см и 6 см. Найдите длину биссектрисы прямого угла.
Дано: 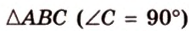
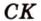
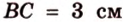
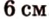
Найти: 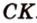
Пусть 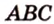
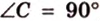
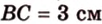
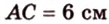
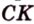
Введем обозначение: 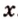
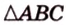
Площадь 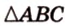
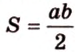
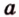
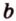
Биссектриса разделила 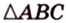
где 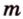
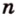
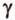
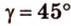
Поскольку 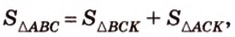
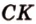
Метод векторов
Чтобы применить метод векторов к решению задачи, необходимо выполнить следующие действия:
Пример №8
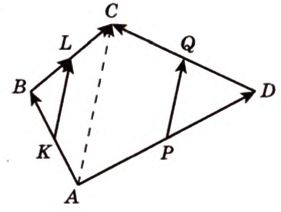
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 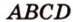
Доказать: 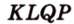
1. Переведем задачу на язык векторов, заменив отрезки векторами: 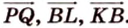
2. Воспользуемся правилом треугольника для сложения векторов: 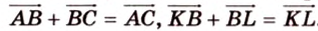
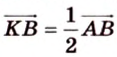
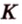
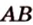
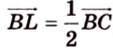
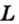
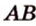
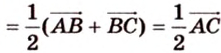
Поэтому 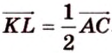
Аналогично 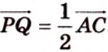
3. Поэтому 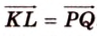
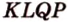
Переведя задачу на язык векторов, получаем требование задачи: доказать равность векторов 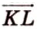
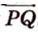
Однако 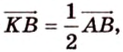
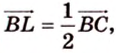
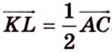
Аналогично получаем, что 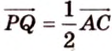
Таким образом, 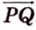
Метод координат
Решая задачу координатным методом, следует выполнить такие действия:
Методом координат чаще всего решают задачи:
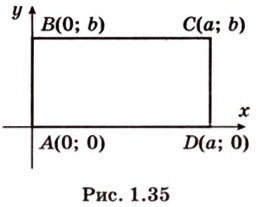
Решая задачу методом координат, необходимо рационально выбрать систему координат: данную фигуру следует разместить относительно осей координат таким образом, чтобы как можно больше координат нужных точек равнялось нулю, а также одному и тому же числу. Например, координаты вершин прямоугольника 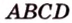
Проиллюстрируем суть метода координат на примере.
Пример №9
Докажите, что когда у параллелограмма диагонали равны, то он прямоугольник.
Разместим параллелограмм в системе координат таким образом, чтобы его вершины имели координаты: 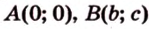
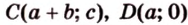
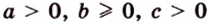
По условию 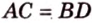
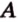
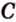
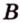
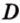
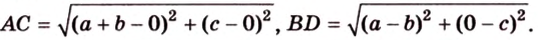
Тогда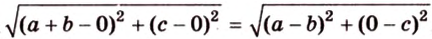
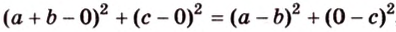
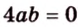
Поскольку 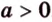
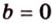
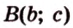
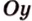
Поэтому угол 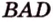
Метод геометрических преобразований: метод поворота, метод симметрии, метод параллельного переноса, метод гомотетии.
Решая задачи методом геометрических преобразований, наряду с данными фигурами рассматривают новые, полученные из данных с помощью определенного преобразования. Выясняют свойства новых фигур, переносят эти свойства на данные фигуры, а затем находят способ решения задачи.
Говорят, что задачи, решенные методами векторов, координат, геометрических преобразований, площадей и другими методами, в которых используется больше свойств геометрических фигур, решены геометрическими методами.
Второй период — формирование геометрии в структурную систему. В VII в. до н.э. центром развития геометрии стала Греция. Древние геометры работали над систематизацией накопленных и новых знаний, устанавливали связи между геометрическими фактами, разрабатывали приемы доказательств. Значительный вклад в развитие математики, в частности геометрии, в этот период сделали Пифагор, Платон, Аристотель, Фалес, Анаксигор, Демокрит, Евклид. В книге «Начала» Евклида сформулированы понятия о фигуре, о геометрическом утверждении и доказательстве. Они остаются актуальными и сегодня.
Особенность начатого Н.И. Лобачевским периода в истории геометрии состоит в том, что после его открытия начали развиваться новые геометрические теории, новые «геометрии» и соответствующие обобщения самого предмета геометрии. В этот период возникло понятие о разновидностях пространства (термин «пространство» в науке может означать как обычное реальное пространство, так и абстрактное, «математическое», пространство). Некоторые теории создавались внутри евклидовой геометрии, как ее особые разделы, а позднее приобретали статус самостоятельных. Другие, подобно геометрии Лобачевского, вводили изменения аксиом и структурировались на основе этих изменений, обобщая и строя науку.
В школьном курсе мы изучаем геометрию Евклида. Перевел труд древнегреческого ученого «Начала» украинский математик Михаил Егорович Ващенко-Захарченко (1825-1912) в 1880 г. На основе этой книги написано множество учебников по геометрии. Например, преподавание геометрии в советской школе почти до 1982 г. осуществлялось по учебнику российского педагога-математика А.П. Киселева (1852-1940). В 1980-х годах украинским математиком А.В. Погореловым было создано новое учебное пособие. Его и сегодня можно найти в библиотеках общеобразовательных учебных заведений.
Современная геометрия является многовекторной и стремительно развивается в совокупностях математических теорий, изучающих различные пространства и их фигуры. Значительный вклад в геометрию сделали и наши соотечественники: М.В. Остроградский, А.М. Астряб, А.П. Киселев, А.Д. Александров, А.Н. Колмогоров, А.В. Погорелов и др.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.