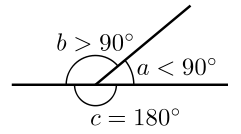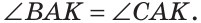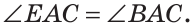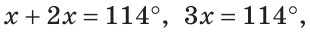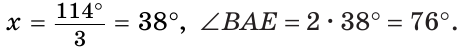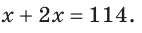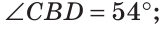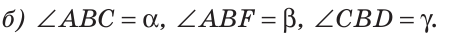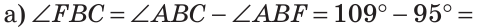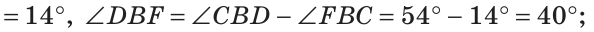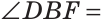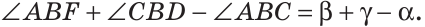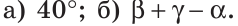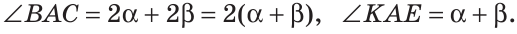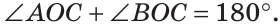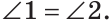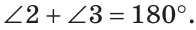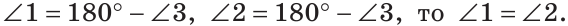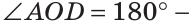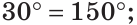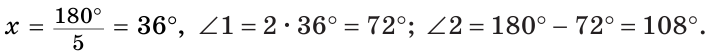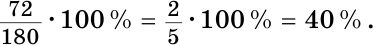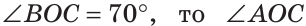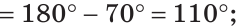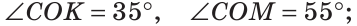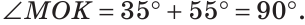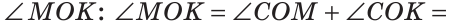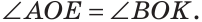Слово Как пишется развернутый угол - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Развернутый угол

Что такое развёрнутый угол — понятие и обозначение

Развернутым называют угол со сторонами, лежащей на одной прямой.

Стороны развернутого угла взаимно дополняют друг друга. В результате получается прямая линия. Таким образом, стороны данной геометрической фигуры представляют собой дополнительные лучи. К примеру, на рисунке изображен ∠CDK, который является развернутым. Точка D служит его вершиной, лучи, обозначенные, как DK и DC – сторонами ∠CDK.

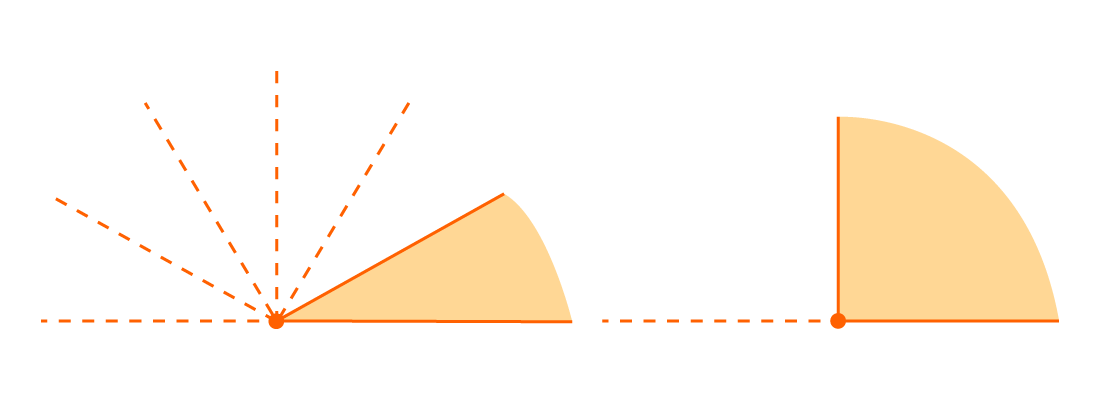
Решить задачу, в которой требуется начертить развернутый угол достаточно просто. Необходимо нарисовать прямую линию и поставить на ней отметку в виде точки, которая будет являться вершиной. Существует другой способ. В начале на плоскости отмечают произвольную точку. Данная отметка будет принята за вершину угла. Если через нее прочертить прямую линию, то получится развернутый угол. Схематично оба способа представлены на рисунке.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определить, является ли угол развернутым, тупым или острым можно с помощью ряда признаков.

Основные свойства развернутого угла:

Геометрические фигуры с развернутыми углами

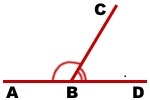
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.

∠ABD в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.

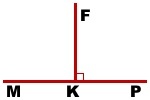
С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.

Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.

Какова градусная мера развернутого угла (сколько радиан)

\(180^<0>\approx 3,14\) радиан.

Точное отношение будет иметь следующий вид:

Примеры решения задач с развернутыми углами

Задача №1

Развернутый угол разделили с помощью луча на две части, которые являются аналогичными геометрическими фигурами. Градусные меры этих элементов относятся, как 1:4. Требуется найти полученные углы.

Решение

Следует обозначить искомые фигуры, как α и β. Предположим, что х является коэффициентом пропорциональности, тогда справедливы равенства:

Зная, что развернутый угол равен 180 градусам, что является суммой градусных мер углов, на которые он разбит с помощью луча, проходящего между его сторонами. Данное утверждение вытекает из свойств этой геометрической фигуры. Можно записать следующую формулу:

Исходя из этого, можно определить углы:

Ответ: после разделения развернутого угла на две части один угол будет равен \(36^<0>\) второй ставит \(144^<0>\)

Задача 2

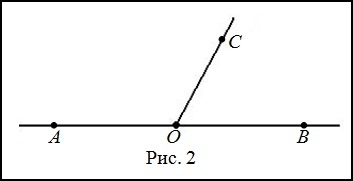
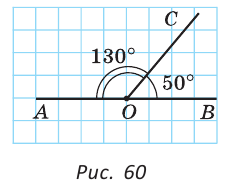
С помощью луча ОС развернутый угол, обозначенный, как АОВ, делят на два угла АОС и ВОС таким образом, что градусная мера угла АОС больше на 30 градусов, чем градусная мера угла ВОС. Требуется найти углы АОС и ВОС.

Решение

Условия задачи следует представить на рисунке:

Допустим, что ∠BOC = x, тогда, согласно условию задачи, получим следующее равенство:

Известно, что образованные углы являются смежными. Таким образом, в сумме эти углы будут составлять \(180^<0>\)

В результате уравнение приобретает следующий вид:

\(x+x+30=180\Rightarrow 2x=150\Rightarrow x^<0>=75^<0>\)

∠BOC=75, откуда следует:

Ответ: угол \(BOC=75^<0>\) угол \(AOC=105^<0>\)

Источник

Что такое угол? Виды углов

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

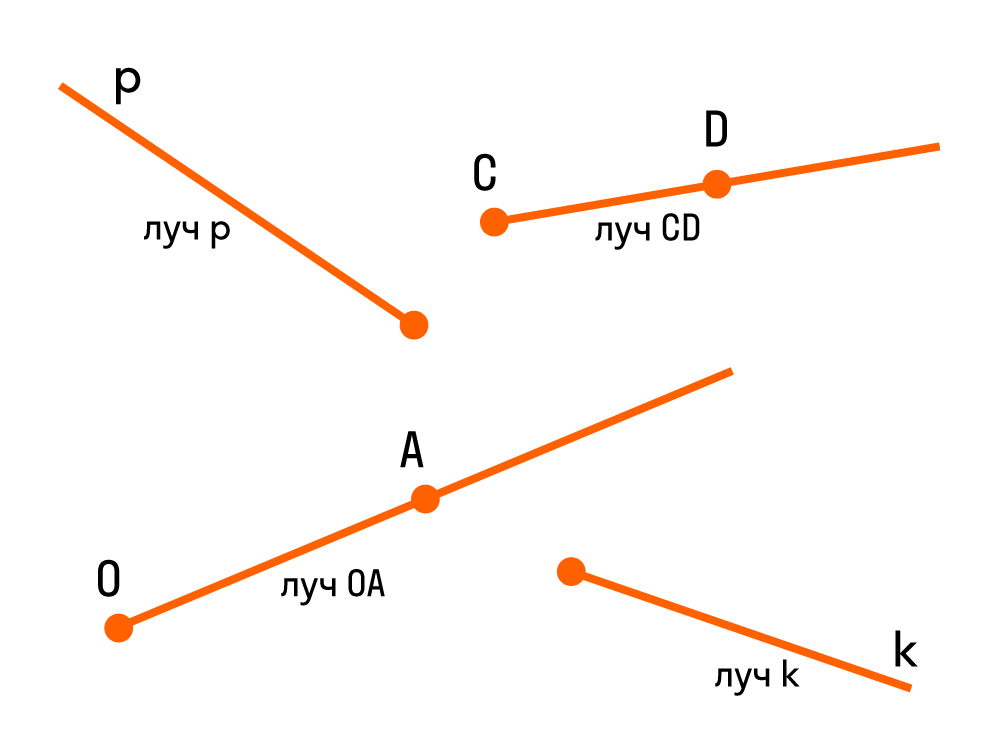
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

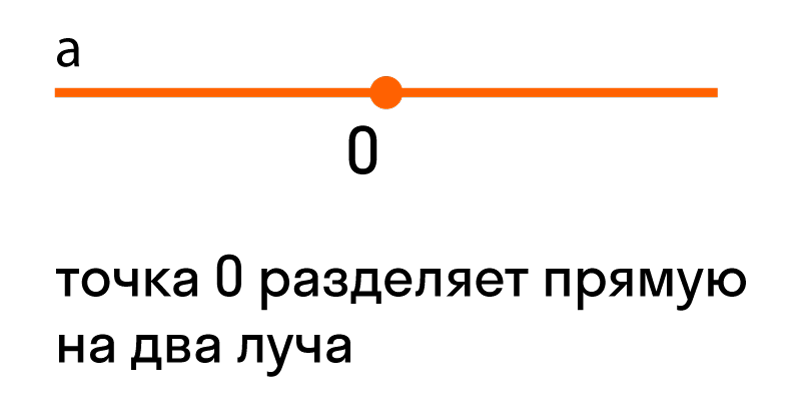
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

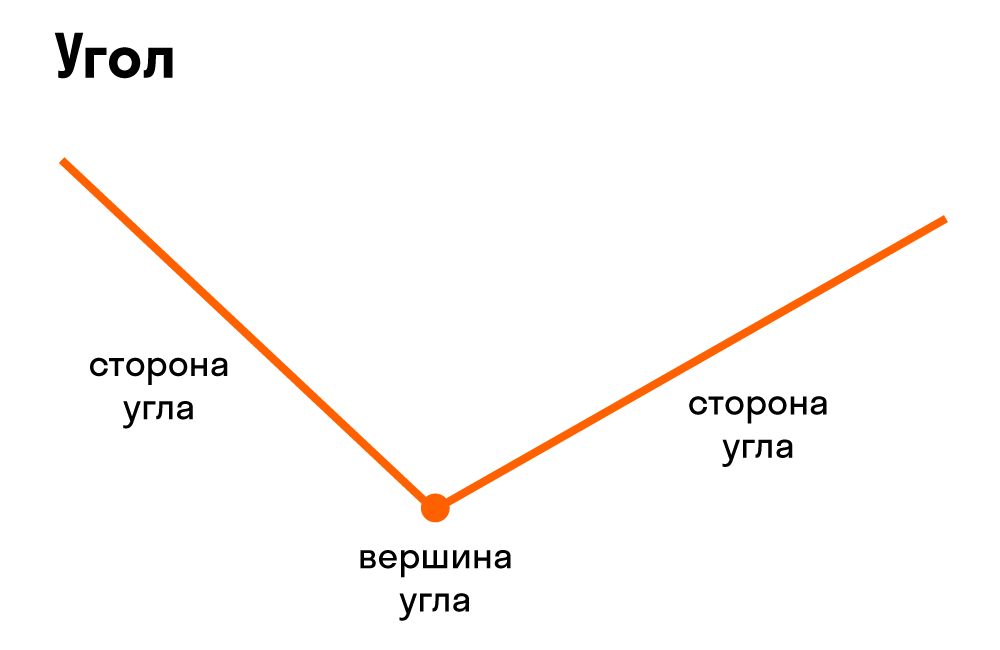
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

Что такое вершина и стороны угла

В математике существует специальный символ для обозначения угла, вот он: ∠.

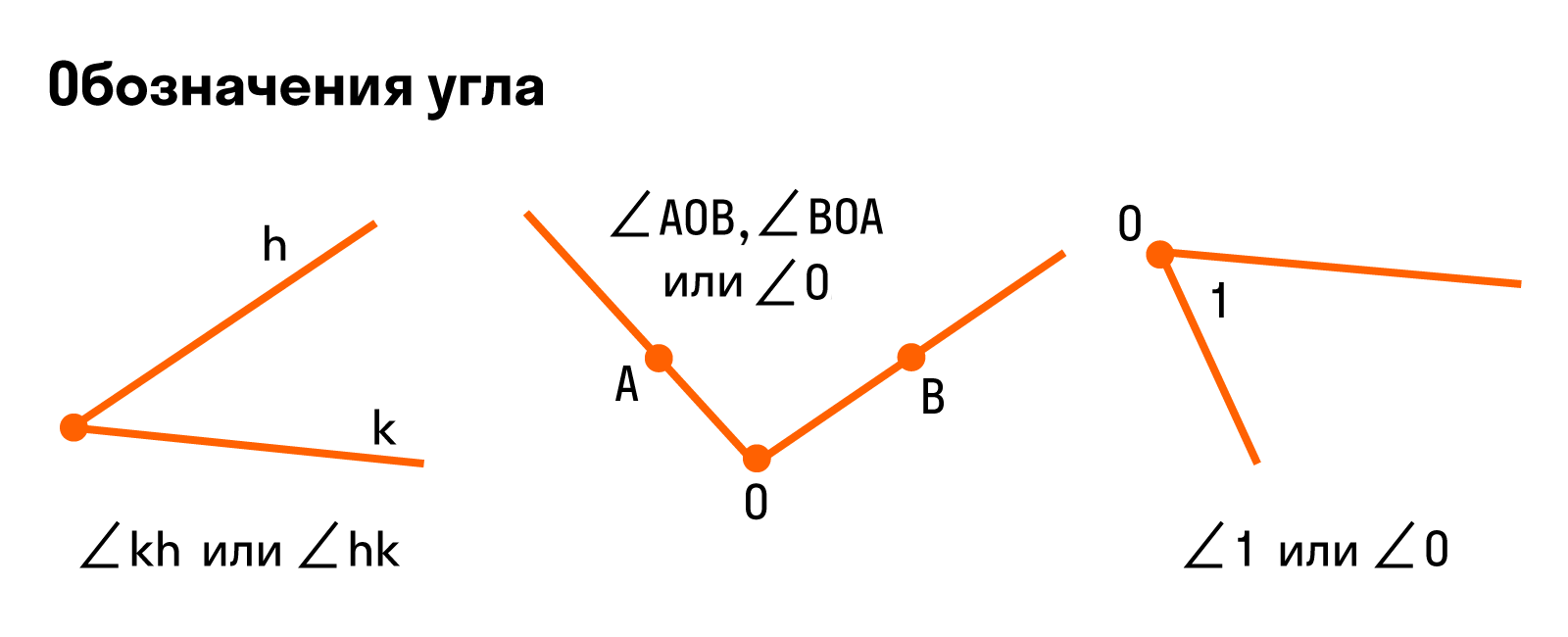
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.

Иногда встречается обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

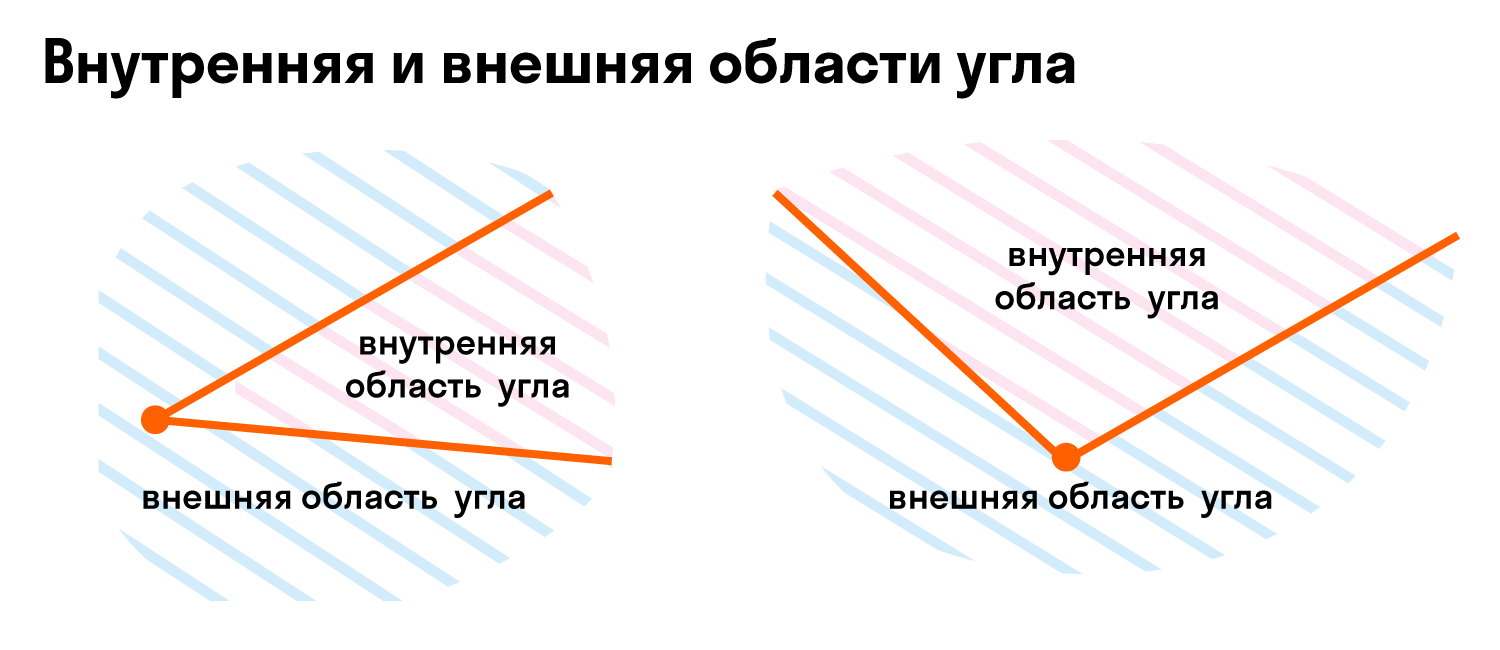
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Виды углов

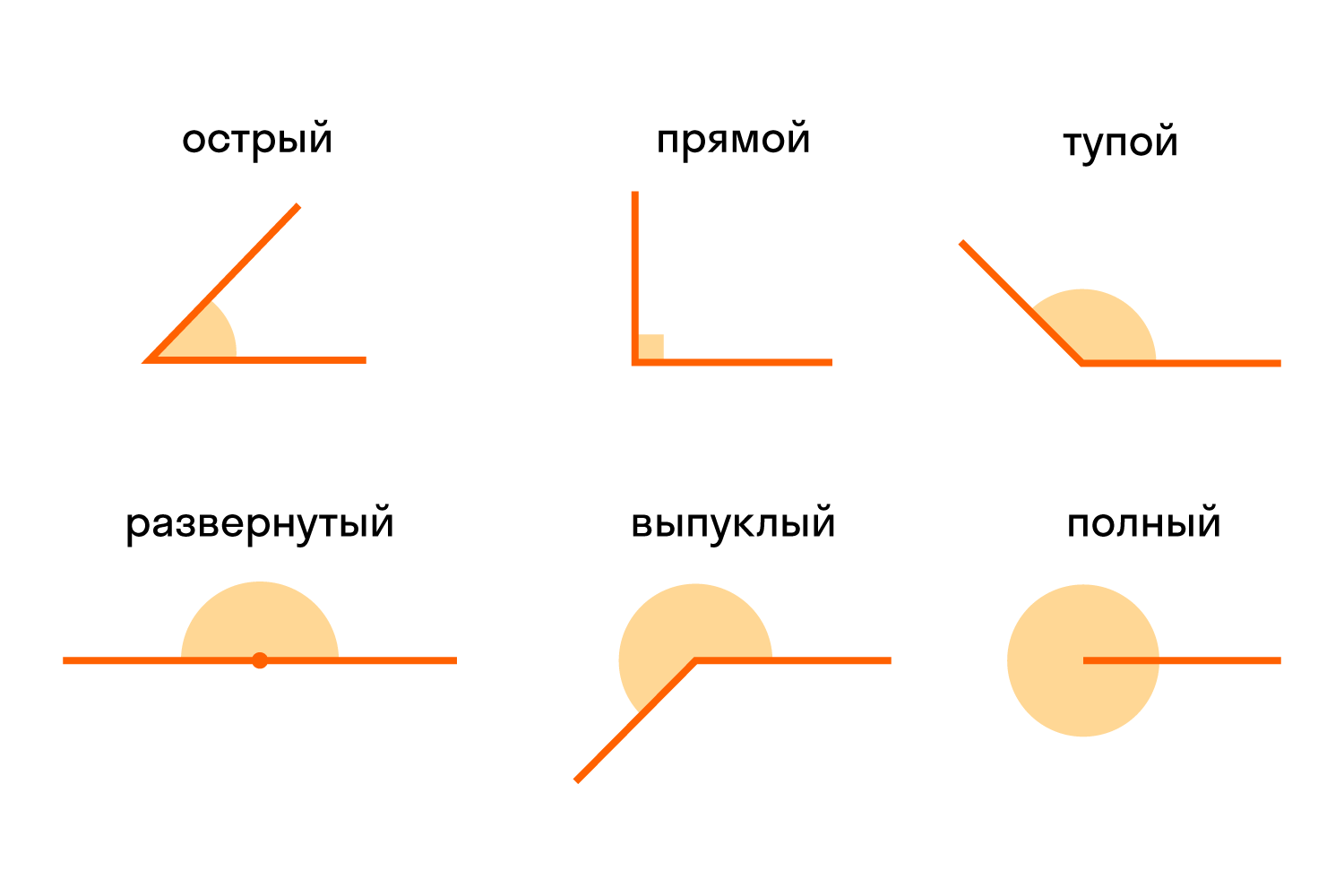
Есть разные типы углов и у каждого своё название:

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

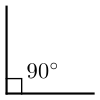
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.

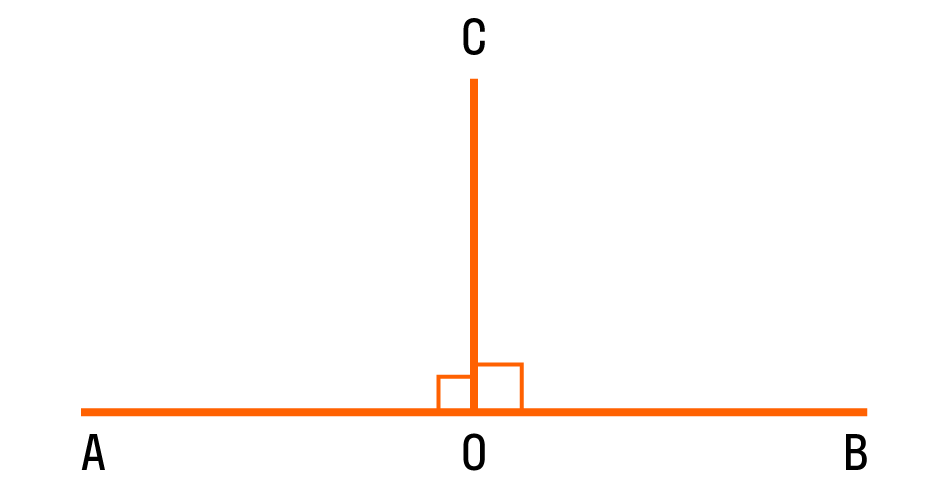
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Острый угол — это угол, который меньше прямого угла, то есть

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Сравнение углов

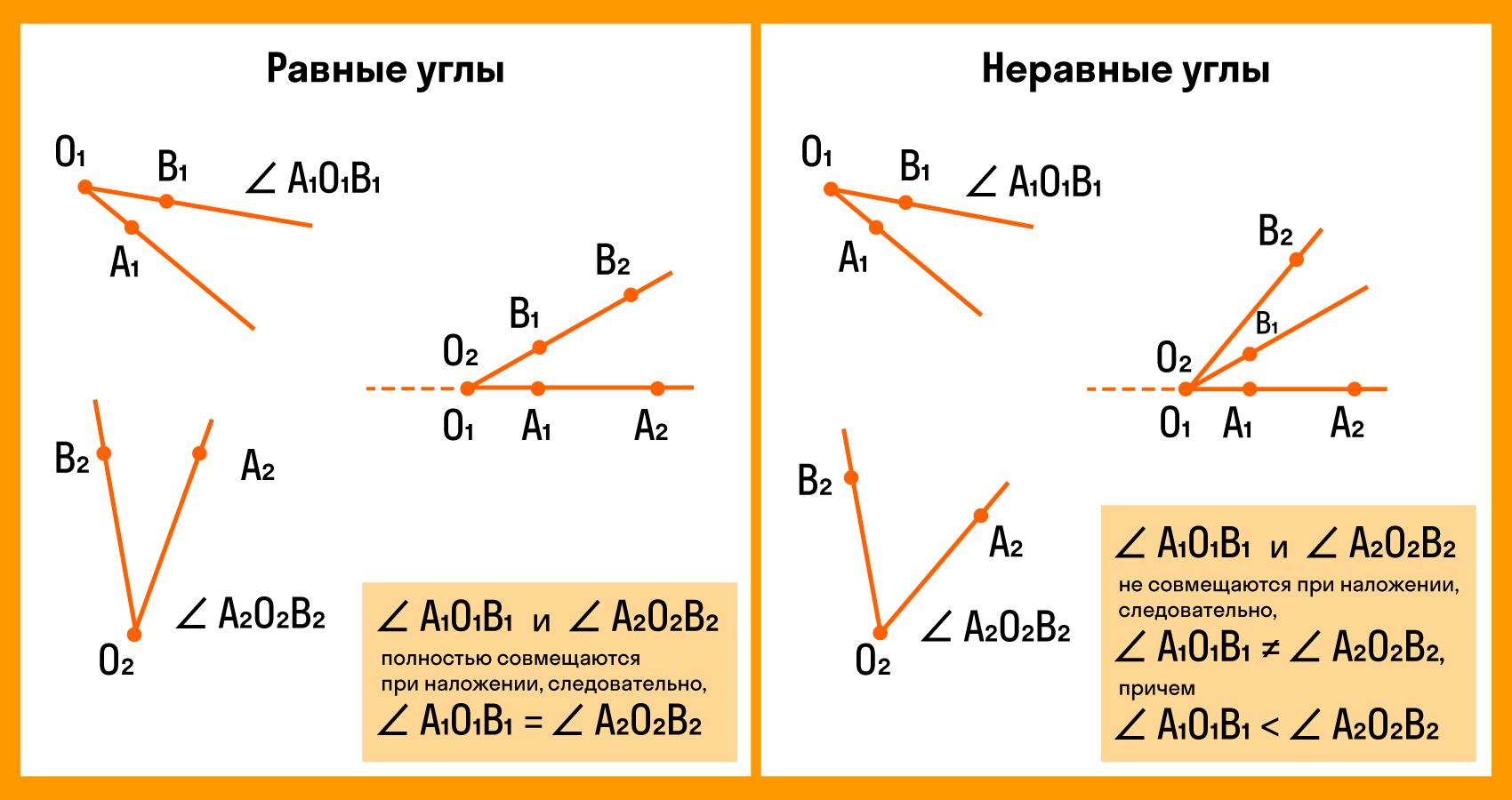
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠??? и ∠??? происходит следующим образом:

Если совпадут и другие стороны, то углы равны: ∠??? = ∠???.

Если нет, то один угол — меньше другого: ∠???

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается ´.

Секунда — 1/60 часть минуты. Обозначается ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.

Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

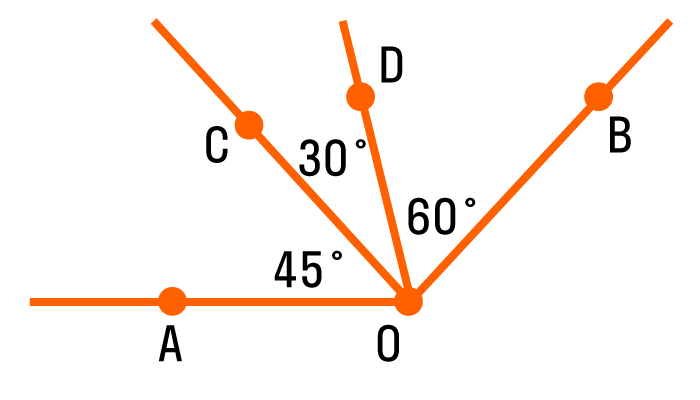
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.

Равные углы имеют равную градусную меру.

Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:

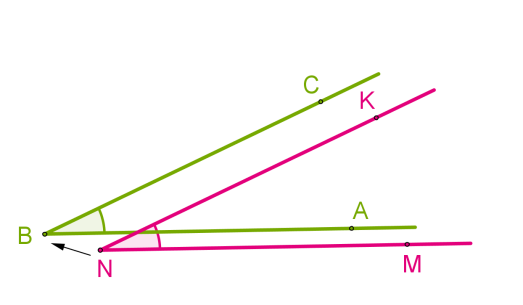
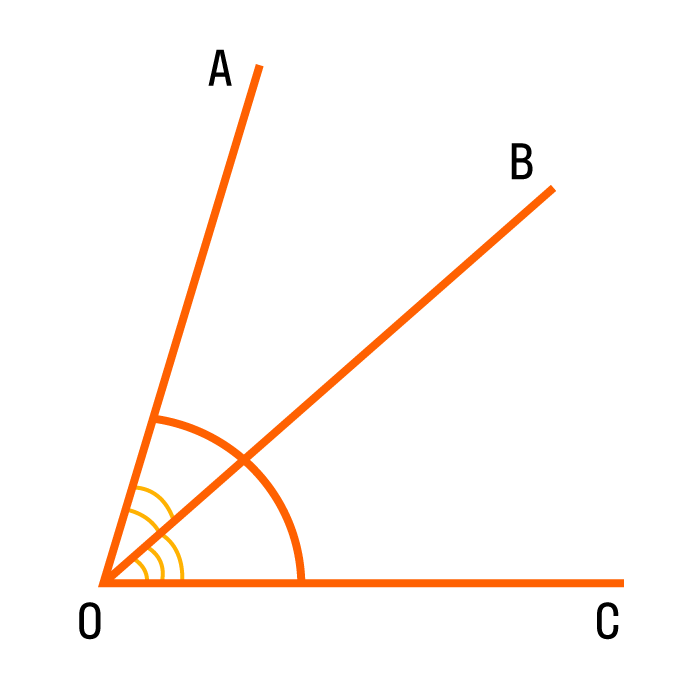
На чертеже отмечены три неравных угла:

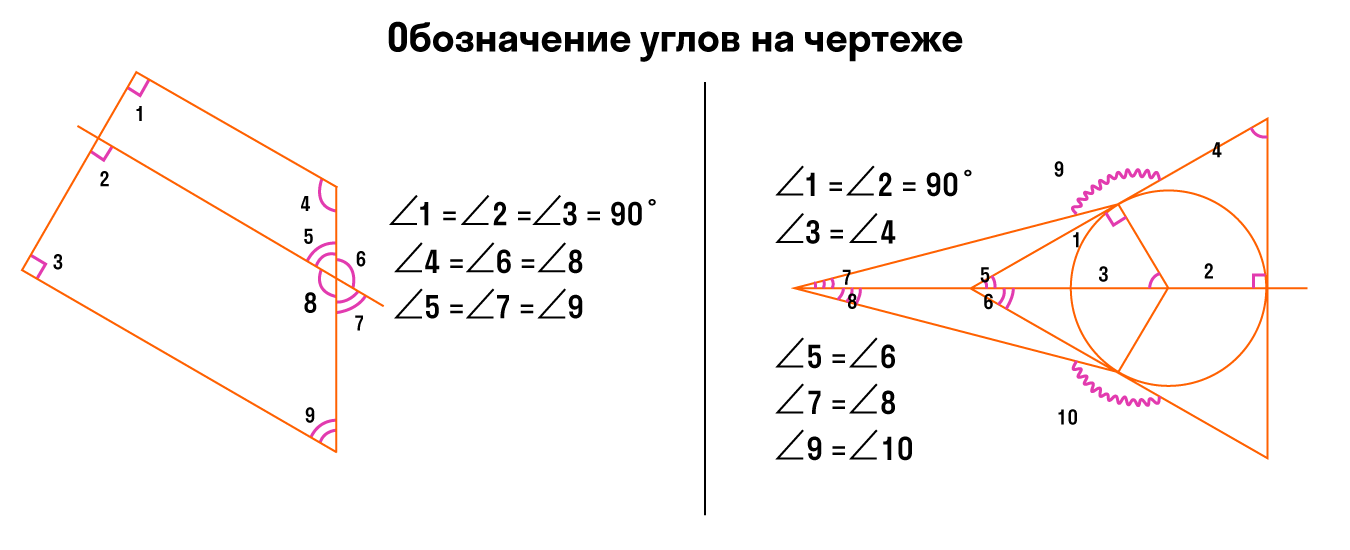
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Источник

Развернутый угол

Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).

Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.

Иногда, для краткости, углом называют угловую меру.

Содержание

Угловая мера

1 оборот = 2π радианам = 360° = 400 градам.

В системе СИ принято использовать радианы.

В морской терминологии углы обозначаются румбами.

Углы на тригонометрической окружности

В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.

В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.

Типы углов

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.

В зависимости от величины углы разделяются на:

Вариации и обобщения

Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).

Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.

Полезное

Смотреть что такое «Развернутый угол» в других словарях:

РАЗВЕРНУТЫЙ УГОЛ — угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь

угол — ▲ разность ↑ направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… … Идеографический словарь русского языка

Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь

УГОЛ — геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия

развёрнутый угол — угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

МНОГОУГОЛЬНИК — 1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия

градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка

Отображение Шварца — Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия

Источник

Как пишется развернутый угол

Основные понятия.

Угол – это фигура, образованная двумя лучами, выходящими из одной точки.

Вершина угла – это точка, из которой выходят два луча, образующих этот угол.

Биссектриса – это луч, который выходит из вершины угла и делит угол пополам.

Развернутый угол – это угол, стороны которого лежат на одной плоскости; равен 180˚ и является прямой.

Прямой угол – это угол, равный половине развернутого угла; равен 90˚.

Острый угол – это угол, который меньше прямого.

Тупой угол – это угол, который больше прямого, но меньше развернутого.

Угол разбивает плоскость на две части. Каждая из частей называется плоским углом.

Плоские углы с общими сторонами называются дополнительными.

Если плоский угол является частью полуплоскости, то его градусной мерой называется градусная мера обычного угла с теми же сторонами.

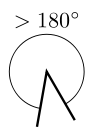
Если плоский угол содержит полуплоскость, то его градусная мера равна 360 º – α, где α – градусная мера дополнительного плоского угла.

Равные углы.

Это углы, которые совпадают при наложении.

Смежные углы.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

На рисунке углы (ad) и (cd) смежные. У них сторона d общая, а стороны a и c – дополнительные полупрямые.

Вертикальные углы.

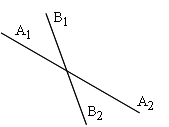
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Они созданы пересечением двух прямых и не являются прилегающими, имеют общую вершину и одинаковую градусную меру.

На рисунке углы (A₁ B₁) и (A₂ B₂) вертикальные. Стороны A₂ и B₂ второго угла являются дополнительными полупрямыми сторон A₁ и B₁ первого угла.

Центральный угол.

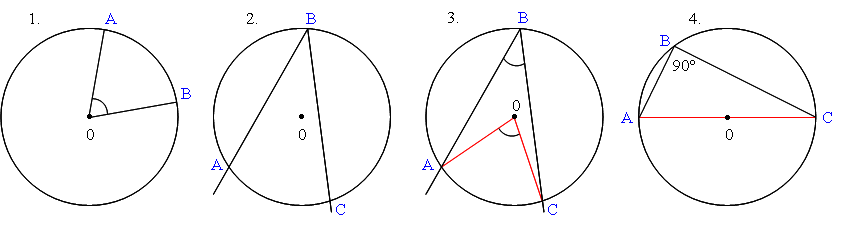
Центральным углом в окружности называется плоский угол с вершиной в ее центре (рис.1).

Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (на рис.1 дуга AB является дугой окружности).

Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Угол, вписанный в окружность.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность (рис.2).

Свойства:

1) Вписанный угол равен половине соответствующего центрального угла (на рис.3 вписанный угол ABC равен половине соответствующего ему центрального угла AOC).

2) Вписанный угол, опирающийся на диаметр, равен 90° (рис.4).

3) Вписанный угол, опирающийся на хорду, равную радиусу окружности, равен 30°.

Углы при пересечении двух прямых третьей.

При пересечении прямых a и b секущей c образуется восемь углов, которые на рисунке обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Источник

Содержание:

Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.

Два угла называются равными, если их можно совместить наложением.

Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.

Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.

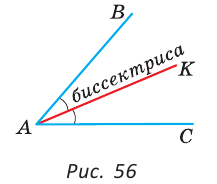
На рисунке 56 луч АК — биссектриса угла ВАС и

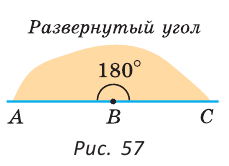
На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.

Углы измеряются в градусах, минутах, секундах.

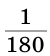
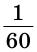
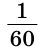
Развернутый угол равен 180°; часть развернутого угла называется градусом и обозначается 1°; часть одного градуса называется минутой и обозначается 1′; часть минуты называется секундой и обозначается 1″.

Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35».

Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».

Определения

Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.

Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).

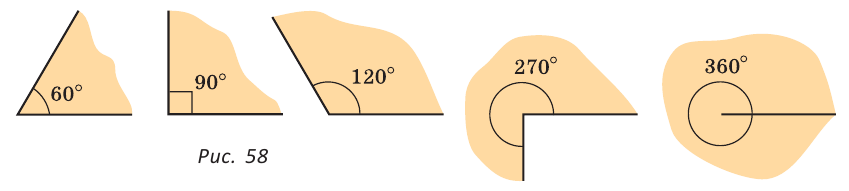
На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.

Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.

Аксиомы

Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.

Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.

Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.

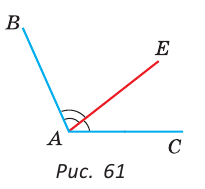
Пример №1

Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.

Решение:

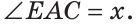
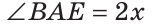
Пусть Тогда (рис. 61).

По аксиоме измерения углов

Тогда

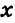
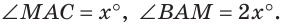
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой пишут знак градуса: Тогда в уравнении знак градуса писать не нужно:

2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.

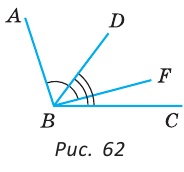
Пример №2

Внутри угла проведены лучи BD и BF (рис. 62).

Найти величину угла DBF, если:

Решение:

Если сложить углы ABF и CBD, то получим угол ABC плюс угол DBF.

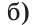
Отсюда

Ответ:

Пример №3

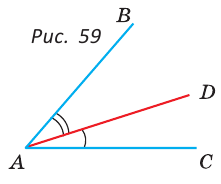
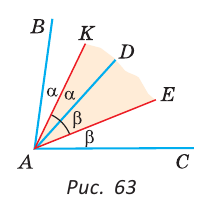
Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).

Доказательство:

Так как АК иАЕ — биссектрисы, то 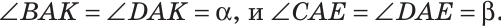Тогда

Следовательно, 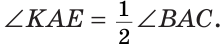Что и требовалось доказать.

Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».

Геометрия 3D

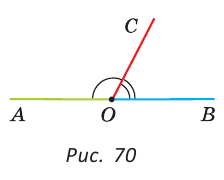
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.

Геометрия 3D

В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 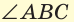— линейный угол изображенного двугранного угла.

Смежные углы. Вертикальные углы

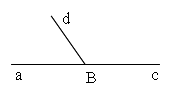
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.

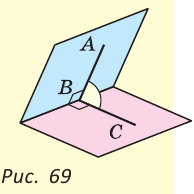
Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.

Теорема (свойство смежных углов). Сумма смежных углов равна 180°.

Дано: 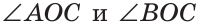— смежные.

Доказать:

Доказательство:

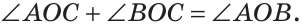
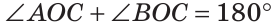
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов Поэтому . Теорема доказана.

Следствия.

Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.

Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.

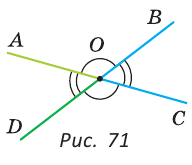
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.

Теорема (свойство вертикальных углов). Вертикальные углы равны.

Дано: 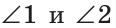— вертикальные (рис. 72).

Доказать:

Доказательство:

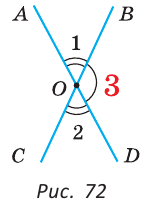
Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов 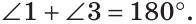Углы 2 и 3 также смежные,

Так как

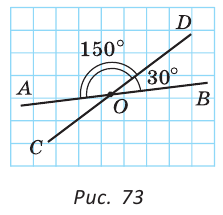
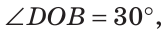
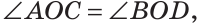
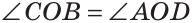
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73) то как вертикальные. Угол между прямыми АВ и CD равен 30°. Говорят, что прямые пересекаются под углом 30°.

При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.

Угол между параллельными прямыми считается равным 0°.

Пример №4

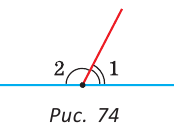
Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.

Решение:

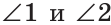
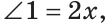
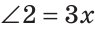
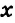
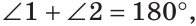
а) Пусть — данные смежные углы (рис. 74). Согласно условию (градусную меру одной части принимаем за ). По свойству смежных углов

то есть

б) Меньшим является 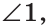а 72° от 180° составляют

Пример №5

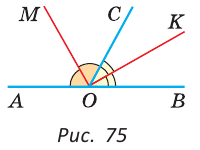
а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если 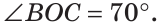б) Доказать, что биссектрисы смежных углов образуют прямой угол.

Решение:

а) Если

б) Так как ОМ и ОК — биссектрисы, то

Найдем градусную меру По свойству смежных углов Тогда . Что и требовалось доказать.

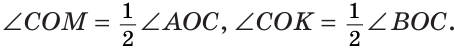
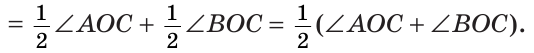
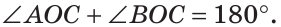
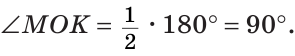
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.

Пример №6

Доказать, что биссектрисы вертикальных углов образуют развернутый угол.

Решение:

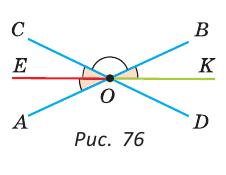
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что — развернутый. Известно, что биссектриса делит угол пополам. Так как вертикальные углы равны, то равны и их половины. Поэтому

б) так как лучи OA и ОВ дополнительные, и поэтому — развернутый. Заменив в последнем равенстве на равный ему получим Отсюда следует, что — развернутый.

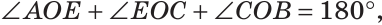
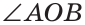
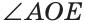
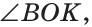
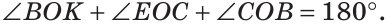
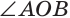
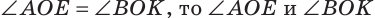
Замечание. Из решения задачи следует свойство: если — развернутый и — вертикальные.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник