Что такое пропорция
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
a и d — крайние члены пропорции, b и с — средние члены пропорции.
Читается это выражение так: a так относится к b, как c относится к d
Например:
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным?
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d
a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
Факультативный курс по математике «Графы» для 5-6 классов
Факультативный курс по математике 5-6 классов «Графы» содержит теорию по теме «Графы» и задания с подробным разбором.
Просмотр содержимого документа
«Факультативный курс по математике «Графы» для 5-6 классов»
Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа №2
города Азова Ростовской области
Факультативный курс по математике
«Графы» для 5-6 классов
Данькова Валентина Николаевна
Тема графов очень интересна при изучении, что позволяет привлечь школьников к активной познавательной деятельности. Графы, как никакая другая модель, позволяет изучать свойства отношений в «чистом виде», а графическое представление решения логических задач делает этот процесс более наглядным. С помощью графов решать задачи очень удобно, интересно, увлекательно, можно рассмотреть несколько вариантов решения одной и той же задачи и выбрать наиболее легкое, удобное, красивое, интересное решение задачи.
Начальные сведения о графах как геометрических схемах, состоящих из точек (вершин) и соединяющих их линий (ребер), достаточно просты, а работа с ними вызывает у детей большой интерес.
В школьном курсе математики теория графов не рассматривается, но в учебниках начальных классов и основной школы, можно встретить задачи, которые намного проще решить с помощью графов, нежели другими способами. Олимпиадные задачи и некоторые задачи ЕГЭ тоже наполнены заданиями, которые легче решить, применяя графический способ. Но что мешает учителю включить в факультативный курс теорию графов и показать, как с ее помощью можно быстро решать «сложные» задачи. Тем более, что некоторый теоретический материал доступен для понимания детей уже даже начальной школы.
Задачи по теории графов можно предлагать не только детям, посещающим факультативы, но и на некоторых уроках математики для развития логического мышления. Но вводить такие задачи нужно постепенно, начиная с элементарных заданий, даже почти с устных, и постепенно повышать уровень их сложности. Конечно, для неподготовленных детей, такие задачи сначала вызовут затруднения в решении, и поиск решения может занимать достаточно долгое время. Поэтому на первых этапах задачи по графам лучше всего задавать, как дополнительное домашнее задание, но не обязательное для всех учащихся. При первом «домашнем» знакомстве с такими упражнениями учителю не обязательно сообщать детям, что при их решении применяется теория графов. Новый неизвестный термин может психологически оттолкнуть детей от поиска решения: «я не решу, ведь мы этого не проходили», хотя и решение может быть совсем легким, элементарным. Лишь только когда дети почувствуют силу при решении задач, можно сказать детям, что эти задания выделяют в особый раздел математики – топологию, теорию графов. Особенно важно, на этом этапе, похвалить тех детей, которые решали или пытались решать задачи, и сказать всему классу, что в их силах решать даже некоторые задачи по неизвестной теме. В дальнейшем можно раз в неделю уделять по 5 минут в конце уроке для дальнейшего изучения теории графов. Но более детальное рассмотрение темы, всё же, надо вынести на факультативный курс.
Для школьника не обязательно давать строгое определение графа, как математического объекта. Им вполне достаточно будет сформулировать несколько определений и теорем и показать, как они работают при решении задач.
Итак, сформулируем основные определения и теоремы на которых можно построить факультативный курс по графам.
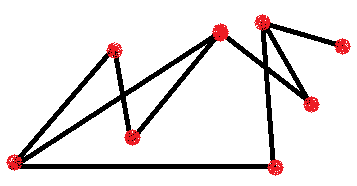
Граф – это набор точек, некоторые из которых соединены линиями.
Особо важно обратить внимание детей в определении на том, что могут соединяться не все точки друг с другом и соединяются не обязательно отрезками, а произвольными линиями-дугами. Далее целесообразно подкрепить новое определение примерами – наглядными рисунками.
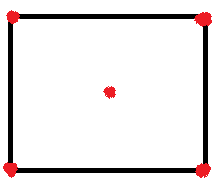
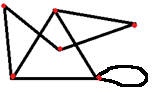
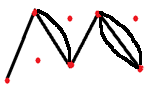

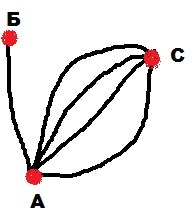
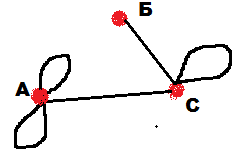
На вышеприведенных примерах очень удобно ввести следующие понятия: вершины (точки) и ребра (линии, соединяющие вершины) графа и закрепить эти понятия на примерах. Четкого, строгого обозначения вершин не существует, обозначают из контекста задачи: или буквами (русскими, латинскими) или цифрами. Причем нужно особо подчеркнуть, что бывают графы, состоящие только из одних вершин (рис.5), что две вершины могут быть соединены несколькими ребрами одновременно (рис.4) и что ребро может «выходить и заходить» в одну и ту же вершину (рис.3) – такое ребро называют петлей.
Графы бывают конечные (число его ребер конечно) и бесконечные (число его ребер бесконечно). В начальной школе и 5-6 классах задачи на бесконечные графы не предлагают, но для детей постарше можно привести пример такого графа. Например, когда каждой вершине графа соответствует натуральное число, т.е. вершины графа нумеруются числами 1, 2, 3… Но так как ряд натуральных чисел бесконечен, то и граф тоже бесконечный. Конечно, полностью изобразить бесконечный граф нельзя, но можно изобразить его частично.
Степень вершины – число ребер выходящих из вершины графа. Если ребро является петлей, то его считают дважды. Закрепляем определение примерами (см. рис.1-5).
Иногда степень вершины записывают в виде таблицы, а иногда пишут рядом с самой вершиной. Важно подчеркнуть, что одно и тоже ребро считается дважды (один раз – для одной вершины, второй – для другой), так как оно соединяет две вершины.
Вершины бывают четные (степень вершины четна) и нечетные (степень вершины нечетна).
Первые задания, которые можно предлагать по теме графы, связаны как раз с этими понятиями: построить граф, определить по рисунку, сколько вершин, ребер у граф, какова степень вершины графа, посчитать сколько четных и нечетных вершин и тому подобные задания. Такие задания можно предлагать и в начальной школе, так как они вполне доступны детям 3-4 классов.
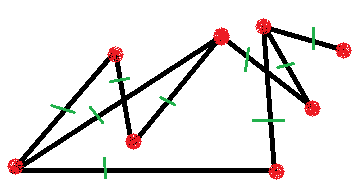
Задание: По рисунку определить: сколько вершин, ребер у графа и какова степень каждой вершины графа?
Решение: Сначала посчитаем количество вершин. Для наглядности на первых порах их можно выделить другим цветом – 8 вершин (рис.8). Для подсчета ребер удобно посчитанное ребро выделять черточкой, чтобы не посчитать его дважды – 9 ребер (рис.9)
Для определения степени вершины графа лучше все вершины обозначить буквами (рис.10), а потом результаты записать в таблицу.
Первое свойство, которое вводим детям без доказательства: «Число нечетных вершин графа – четно». И в дальнейшем, все свойства и теоремы даются без строгого доказательства. Закрепление данного свойства происходит так же на решении задач.
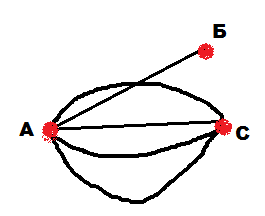
Задание: Построить граф у которого вершины имеют следующие степени:
а) А – 7, Б – 3, С – 1; б) А – 5, Б – 1, С – 4.
Решение: При решении задач на построение графов, надо объяснить детям, что сначала необходимо проверить, возможно ли вообще построение заданного графа. Для этого учащиеся должны применить первое свойство. Сколько бы дети не пытались построить граф а), у них ничего не получится. Построение графа а) невозможно, так как все его вершины нечетные, и число их нечетно. А вот граф б) построить можно, так как у него две нечетных вершины. Причем у детей могут получаться различные по конфигурации графы (рис.11-13). Именно на таких заданиях и закрепляется, что число нечетных вершин графа – четно.
Поучительная сторона этих задач состоит в исследовании, возможно или нет решение данной задачи, прежде чем приниматься за само решение.
Обратите внимание детей, что построение графа следует начинать с изображения всех его вершин, и лишь потом соединять их ребрами. Причем лучше всего начинать соединять ребрами вершины с наименьшей и наибольшей степенью.
Далее лучше всего дать задания такого плана: «без построения графа, определить число ребер графа».
Свойство 2: Для того чтобы найти количество ребер в графе, надо просуммировать степени вершин и результат разделить пополам.
Задание: Даны степени вершин графа: А – 2, Б – 5, С – 1, Д – 4. Без построения графа, определить число ребер графа.
Решение: Первое, что должны проверить дети: возможно ли построение такого графа. Чтобы проверить это, надо сосчитать число нечетных вершин – их должно быть четно. По условию задачи 2 нечетных вершины Б и С, значит построение возможно. Теперь можно ответить на вопрос задачи, используя второе свойство: (2+5+1+4):2=6.
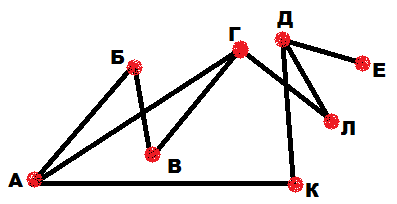
Три друга Алеша, Боря и Вова после школы едут домой на различном транспорте: автобусе, маршрутке, трамвае. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходила маршрутка, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!» Кто на чем ездит домой?
Решение: Задача отличается от предыдущей задачи тем, что в ней несколько ключевых фраз, но решается тоже с построением несвязного графа (рис.48), который содержит 6 вершин и 3 ребра. Первая ключевая фраза, которая помогает решить задачу: «Алеша пошел проводить своего друга до остановки автобуса», значит Алеша ездит не на автобусе. Вторая ключевая фраза: «Когда мимо них проходила маршрутка», значит Алеша ездит не на маршрутке. Остается – Алеша на трамвае. Третья ключевая фраза: «третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!»», значит друг, которого провожал Алеша до автобуса – Боря, а Вова едет на маршрутке. Ребра и показывают ответ задачи.
Решение: В данной задаче граф будет состоять из 8 вершин и 4 ребер. Первая ключевая фраза, которая помогает решить задачу: «Журналист написал статьи об Андрее, Борисе и Грише», значит журналист это Витя. Вторая ключевая фраза: «Тренер и журналист вместе с Борисом ходили в поход», значит Борис не тренер и не журналист. Третья ключевая фраза: «Андрей и Борис были на приеме у врача», значит врач не Андрей и не Борис. Так как больше с условием задачи работать нельзя, то будем работать по графу. По графу видно, что Борис не врач, не журналист, не тренер, а значит – строитель (рис.49). Андрей – не врач, но и не журналист (Витя) и не строитель (Борис), а значит – тренер. А Грише остается врач. Ребра и показывают ответ задачи (рис.50).
Решение: В данной задаче граф будет состоять из 9 вершин и 6 ребер. Причем вершины надо разбить на три тройки: первая – имена, вторая – цвет туфель, третья – цвет платья и разместить их для наглядности в разных плоскостях (рис.51). Первая ключевая фраза, которая помогает решить задачу: «Валя была в белых туфлях», значит проводим первое ребро от Вали до белых туфель. Вторая ключевая фраза: «Ни платье, ни туфли Лиды не были красными», значит проводим пунктиры от Лиды до красных туфель и красного платья. Третья ключевая фраза: «Только у Тамары цвета платья и туфель совпадали», значит у Вали не белое платье (так как у нее белые туфли). Так как больше с условием задачи работать нельзя, то будем работать по графу (рис.52). По графу видно, что у Лиды голубые туфли (так как красные быть не могут, а белые у Вали), значит, проводим второе ребро. Далее видно, что Тамаре остаются красные туфли и значит и красное платье (третья ключевая фраза), проводим еще два ребра. У Вали голубое платье (так так красное у Тамары, а белое не может быть по графу). Остается Лиде белое платье, проводим последнее ребро. Ребра и показывают ответ задачи (рис.53).
Алла решила маме на день рождения подарить букет цветов (розы, тюльпаны или гвоздики) и поставить их или в вазу или в кувшин. Сколькими способами это можно сделать?
Решение: Решением задачи будет несвязный граф, состоящий из трех граф-деревьев (рис.56). Первым звеном графа будут цветы, вторым – сосуды. По графу легко составить все возможные комбинации букетов: Р-В, Р-К, Т-В, Т-К, Г-В, Г-К – 6 способов. рис.56
.
Проанализировав выше предложенный практический материал, приходим к выводу, что для решения задач, с применением теории графов, можно выделить следующие этапы:
Анализ условия задачи и перевод ее на язык графов;
Геометрическая интерпретация условия, построение графа. Именно на этом этапе очень важен элемент творчества потому, что далеко не просто найти соответствия между элементами условия и соответствующими элементами графа;
Точками обозначают объекты задачи (вершины графа). Если в задачах дано несколько групп объектов, то лучше их изображать в разных плоскостях и различными цветами;
Выделяем ключевые фразы задач и, анализируя их, проводим ребра;
Если ключевых фраз не достаточно для решения задачи, то анализируем граф и проводим недостающие ребра;
Выбираем нужные отношения (сплошные линии) и записываем ответ.
Использование графов в качестве некоторого вспомогательного средства позволяет облегчить процесс обучения и подготовить учеников к восприятию сложных тем в курсе школьной математики. Графовые задачи, без сомнения, нужно использовать не только на математических кружках, при подготовке к олимпиадам для развития сообразительности учеников, но и использовать теорию графов как языка на уроках математики, алгебры, геометрии, информатики для повышения качества обучения.
Таким образом, применяя теорию графов в школьном курсе математики, решение многих математических задач и доказательств упрощается, придает им наглядность и простоту.
Урок 21 Бесплатно Отношения
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Отношение
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как \(\mathbf\) или же через дробную черту: \(\mathbf<\frac>\)
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в \(\mathbf<1\frac<1><4>>\) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в \(\mathbf<\frac<2><3>>\) раза.
Мы можем сформулировать вывод и так: 16 составляет \(\mathbf<\frac<2><3>>\) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
И посчитаем отношение 28 к 14
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно \(\mathbf<\frac<2><5>>\), найдем отношение b к a
Для этого надо найти обратное число к \(\mathbf<\frac<2><5>>\)
Значит, отношение b к a равняется \(\mathbf<2\frac<1><2>>\)
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно \(\mathbf<\frac<1><3>>\)
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно \(\mathbf<\frac<1><3>>\)
Пройти тест и получить оценку можно после входа или регистрации
Отношение и часть от числа
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него \(\mathbf<\frac<3><8>>\)
Перемножив, мы получим:
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна \(\mathbf<2\frac<1><2>>\)
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
Ответ: дробь, взяв которую от 10 получили \(\mathbf<2\frac<1><2>>\), равняется \(\mathbf<\frac<1><4>>\)
Пример 2
Отношение первого числа ко второму равно \(\mathbf<1\frac<1><5>>\), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к \(\mathbf<1\frac<1><5>>\)
Теперь можно найти второе число, домножим первое на эту дробь:
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно \(\mathbf<1\frac<1><2>>\)
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
Ответ: число a равняется 12
Пройти тест и получить оценку можно после входа или регистрации
Отношения в задачах
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
Значит, длина освещенного участка составляет \(\mathbf<\frac<3><5>>\) от длины всей улицы.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
Что отвечает на вопрос второго пункта.
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации