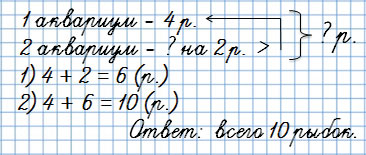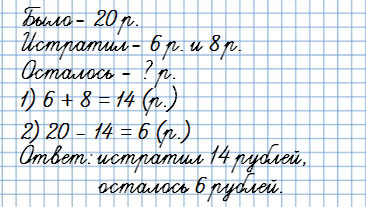Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
Сколько грибов нашёл Володя?
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было. Стало. «
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было. Осталось. «
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали. Осталось. «
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Сколько рыбок в двух аквариумах?
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
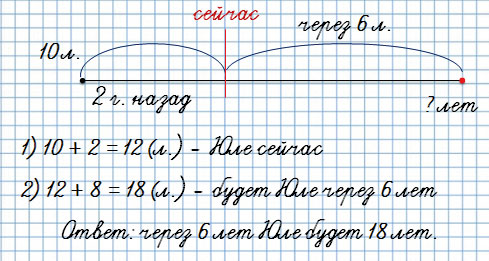
Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Поделись с друзьями в социальных сетях:
СОСТАВНАЯ ЗАДАЧА. ЗАПИСЬ РЕШЕННЫХ ЗАДАЧ.
Составная задача включает в себя ряд простых задач, связанных между собой так, что искомая одних простых задач служит данными другой простой задачи. Последовательность решения простых задач является решением составной задачи.
Решение любой задачи- это процесс сложной умственной деятельности. Чтобы овладеть ими надо знать основные этапы решения задачи и некоторые приемы их выполнения.
Формы записи решенной задачи:
В 1 классе решение составная задача записывается выражение с ответом или без ответа:
· 18-12=6 (яб) Ответ: 6 яблок;
Рассмотрим образцы записи решенной задачи на конкретном примере: В магазине за 8 пар туфель по цене 9 ру. Получили столько же сколько стоило 6 пар ботинок. Сколько стоила 1 пара ботинок?
1. запись решения ввиде выражения:
а) постепенная запись выражения с записью отдельных действий:
(9*8)= 72 (р)- стоим.туфель ли ботинок
(9*8)/6=12 (р)- стоит 1 пара ботинок
б) запись выражения без записи отдельных действий:
Ответ: 12 рублей цена пары ботинок.
Запись решения ввиде отдельных действий
а) запись по действиям с поянением:
1) 9*8= 72 (р)- стоим. Туфель или ботинок;
2) 72/6= 12 (р)- стоит пара ботинок.
б) запись по действиям без заполнения пояснений:
Ответ: 12 рублейстоит пара ботинок.
Запись по действиям с вопросами
— Сколько стоят все туфли и ботинки?
— сколько стоила 1 пара ботинок?
ПРОВЕРКА РЕШЕНИЯ СОСТАВНЫХ ЗАДАЧ. ВИДЫ ПРОВЕРКИ.
Способы проверки р.з.
1. Составление и решение обратной задачи. Суть: одно из искомых величин делают данной, а одну из данных – искомой.
Н-р: На изготовление 5 чайных лож. По 200 гр израсх-ли столько же металла, сколько и на 2 ст.л. Сколько гр металла расх-ли на 1 ложку?
(20*5):2=50 гр масса 1 ст.л.
Сколько ст.л. по 50 гр каждая можно изготовить из металла, которой израс-ли на 5 ч.л. по 20 гр.
Проверка задачи по условию
Суть: после р.з. надо пров-ть каждое число условия, исполь-я рез-т решения и само условие.
Н-р: Ученики собирали 3 мешка картошки. Всего 153 кг. Взвесили 1 и 2 кг, взв-ли 2 и 3 мешка, получили 99 кг. Сколько кг было в каждом?
2. 99-51=48 кг – 2 мешок
3. 102-48=54 кг – 1 мешок
1. 51+48+54=153 – 3 мешка вместе
2. 54+48=102 кг – 1 и 2 мешки
3. 48+51=99 кг. – 2и3 мешки
МЕТОДИКА ИЗУЧЕНИЯ НУМЕРАЦИИ ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
ОЗНАКОМЛЕНИЕ С НАЗВАНИЕМ, ПОСЛЕДОВАТЕЛЬНОСТЬЮ И ОБОЗНАЧЕНИЕМ ЧИСЕЛ В ПРЕДЕЛАХ 10.
Перед тем как начать обучать этому детей, нужно сначала изучить знания детей о названиях чисел, ее последовательности, понятия «больше, меньше, столько же» также их уровень пространственных представлений.
4. Знакомство с печатной и письменной цифрой.
Изучаемые числа обозначают сначала печатными цифрами, которые выставляют на наборном полотне рядом с соответствующим множеством предметов. Учитель поясняет: можно сказать три квадрата, три куклы, три
машины, а можно обозначить число 3 вот таким знаком, такой цифрой. (Показывает.) Для закрепления используют взаимообратные упражнения:
а) учитель называет число предметов, учащиеся показывают цифрой;
б) учитель показывает цифру, учащиеся предметы.
Знакомя с письменной цифрой, учитель объясняет и показывает образец написания на доске. Дети повторяют объяснение вслух, рисуя при этом цифру в воздухе или обводя образец, данный учителем в тетрадях.
5. Сравнение последовательных чисел натуральногоряда и записи вида 4>3, 3
Дата добавления: 2019-07-15 ; просмотров: 932 ; Мы поможем в написании вашей работы!
Виды составных задач. Способы их решения.



Факультет психологии и педагогического образования
Кафедра начального образования
МЕТОДИКА ПРЕПОДАВАНИЯ МАТЕМАТИКИ
1 курса, группы НО-1.19
Практическое занятие
МЕТОДИКА РАБОТЫ НАД ПРОСТОЙ ЗАДАЧЕЙ
Вопросы для обсуждения
Понятие «задача». Классификация простых задач.
Задача— это текст, содержащий численные компоненты.
1-я группа — простые задачи на усвоение конкретного смысла арифметических действий.
В эту группу входят такие задачи:
1) Нахождение суммы двух чисел.
2) Нахождение остатка.
3) Нахождение суммы одинаковых слагаемых (произведения).
4) Деление на равные части.
5) Деление по содержанию.
2-я группа— простые задачи на усвоение связи между компонентами и результатами арифметических действий.
В эту группу входят такие задачи:
1) Нахождение первого слагаемого по известным сумме и второму слагаемому.
2) Нахождение второго слагаемого по известным сумме и первому слагаемому.
3) Нахождение уменьшаемого по известным вычитаемому и разности.
4) Нахождение вычитаемого по известному уменьшаемому и разности.
5) Нахождение первого множителя по известным произведению и второму множителю.
6) Нахождение второго множителя по известным произведению и первому множителю.
7) Нахождение делимого по известным делителю и частному.
8) Нахождение делителя по известным делимому и частному.
3-я группа— простые задачи, раскрывающие новый смысл арифметических действий: понятия разности и кратного отношения.
В эту группу входят такие задачи, связанные с понятием разности:
1) Разностное сравнение чисел или нахождение разности двух чисел (1 вид).
2) Разностное сравнение чисел или нахождение разности двух чисел (2 вид).
3) Увеличение числа на несколько единиц (прямая форма).
4) Увеличение числа на несколько единиц (косвенная форма).
5) Уменьшение числа на несколько единиц (прямая форма).
6) Уменьшение числа на несколько единиц (косвенная форма).
В эту группу также входят простые задачи, связанные с понятием кратного отношения.
1) Кратное сравнение чисел или нахождение отношения двух чисел (1вид).
2) Кратное сравнение чисел или нахождение отношения двух чисел (2 вид).
3) Увеличение числа в несколько раз (прямая форма).
4) Увеличение числа в несколько раз (косвенная форма).
5) Уменьшение числа в несколько раз (прямая форма).
6) Уменьшение числа в несколько раз (косвенная форма).
План работы над простой задачей.
1. Восприятие и первичный анализ задачи.
2. Поиск решения и составление плана решения.
3. Выполнение решения и получение ответа на вопрос задачи.
4. Проверка решения. Формулировка окончательного ответа на вопрос
задачи.
Методы и приемы в работе с простой задачей.
В методике работы на этой ступени выделяются следующие этапы:
Приемы в работе с простой задачей:
1. Представление той жизненной ситуации, которая описана в задаче, мысленное участие в ней.
2. Разбиение текста задачи на смысловые части.
3. Переформулировка текста задачи: замена данного в нём описания ситуации другим, сохраняющим все отношения и зависимости и их
количественные характеристики, но более явно их выражающим.
Задания для самостоятельного выполнения
Разработайте пример простой задачи каждого вида для младших школьников.
I. Задачи, направленные на раскрытие смысла арифметических действий.
1. Задачи на нахождение суммы двух чисел.
Пример. Саша поймал 4 рыбки, а Леша 3 рыбки. Сколько всего рыбок поймали дети?
2. Задачи на нахождение остатка.
Пример. В корзине было 10 морковок. 3 морковки отдали кроликам. Сколько морковок осталось в корзине?
3. Задачи на нахождение суммы одинаковых слагаемых.
Пример. Тетрадь стоит 2 рубля. Сколько стоят три таких тетради?
4. Задачи на деление на равные части.

Пример. 10 тетрадей раздали 5 ученикам поровну. Сколько тетрадей получил каждый ученик?
5. Задачи на деление по содержанию.
Пример. Мама раздала детям 12 яблок, по 4 яблока каждому. Сколько детей получили яблоки?
II. Задачи, раскрывающие связи между компонентами и результатами арифметических действий.
1. Задачи на нахождение неизвестного слагаемого.
Пример. Миша и Саша поймали 10 жуков. Миша поймал 6 жуков. Сколько жуков поймал Саша?
2. Задачи на нахождение неизвестного уменьшаемого.
Пример. У девочки было несколько шаров. Когда она отдала подруге 3 шара, у нее осталось 5 шаров. Сколько шаров было у девочки?
3. Задача на нахождение неизвестного вычитаемого.
Пример. В гараже стояло 8 машин. После того, как несколько машин выехало, в гараже осталось 5 машин. Сколько машин выехало?
4. Задача на нахождение неизвестного множителя.
Пример. Первый множитель 2, второй неизвестен, произведение 8. Найти второй множитель.
5. Задачи на нахождение неизвестного делимого.
Пример. Делитель 2, частное 5. Найти делимое.
6. Задачи на нахождение неизвестного делителя.
Пример. Делимое 12, частное 4. Найти делитель.
III. Задачи, раскрывающие связи между величинами
При решении задач этой группы дети усваивают названия величин и связи между величинами:
а) цена, количество, стоимость;
б) масса одного предмета, количество предметов, общая масса;
в) скорость, время, расстояние;
г) длина, ширина, площадь прямоугольника и др.
МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ СОСТАВНЫХ ЗАДАЧ
Вопросы для обсуждения
1. Понятие «составная задача».
Под составнойпонимают задачу, в решении которой используют два или более действий.
Виды составных задач. Способы их решения.
Виды:
3.Нахождение неизвестного слагаемого.
4.Нахождение неизвестного вычитаемого.
5.Нахождение третьего слагаемого.
6.Нахождение неизвестного уменьшаемого.
При знакомстве с составными задачами учитель должен иметь в виду, что первыми решаются составные задачи только в два действия. Эти задачи могут различаться:
а) количеством данных в них;
б) сочетанием действий, которыми они решаются.
Эти различия между составными задачами в 2 действия могут помочь увидеть детям различия между простыми и составными задачами.
Для первоначального знакомства с составными задачами рекомендуется отбирать задачи, при решении которых надо выполнить два различных арифметических действия: сложение и вычитание. При этом необходимо взять такую задачу, которая понятна детям по содержанию и ее легко проиллюстрировать.
Урок математики составные задачи
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Урок математики 2 класс
Тема: «Знакомство с составными задачами».
познакомить с понятием «составная задача»; научить отличать составные задачи от простых, записывать условие составной задачи в форме краткой записи;
развивать умение моделировать условие задачи с помощью схемы-модели, выявлять отношения между величинами, вести поиск решения задачи; развивать вычислительные навыки, внимание, наблюдательность, сообразительность, абстрактное мышление, положительную мотивацию к обучению;
воспитывать интерес к урокам математики.
Технология: исследовательские методы обучения
Оборудование: таблицы-опоры краткой записи задач, схемы-модели, карточки с выражениями на сложение/вычитание, основанное на знании десятичного состава чисел.
I. Самоопределение к деятельности
Начинается урок.
Он пойдет ребятам впрок.
Постарайтесь все понять,
Учитесь тайны открывать,
Ответы полные давайте
И на уроке не зевайте.
(На доске записана пословица: «Век живи – век учись».)
Учитель: Как вы понимаете эти слова?
(Варианты ответов детей.)
Учитель: Хотите сегодня чему-нибудь научиться?
Дети: Да.
Учитель: Хорошо, приступаем к работе.
(Дети записывают в тетрадях число.)
II. Актуализация опорных знаний и мотивация
Учитель: Чтобы узнать о чём мы сегодня будем говорить, вам придётся найти значение этих числовых выражений.
45 + 20 = а 30 + 47 = з
83 – 60 = и 34 – 3 = ч
50 – 8 = а 43 + 7 = д
(ответы записаны на перевёрнутых листочках, с обратной стороны которых написаны буквы)
Дети записывают числовые выражения в тетрадях и находят их значение.
Учитель: Проверьте друг у друга правильность вычислений.
(Взаимопроверка выполнения задания.)
Учитель: Назовите числа, которые вы получили.
(Дети зачитывают и проверяют. На доске переворачиваются листочки с ответами.)
Учитель: Поднимите руки, у кого нет ошибок. Оцените своё знание вычислительных приёмов «смайликом» на полях.
(Дети выполняют самооценивание.)
Учитель: А теперь расположите полученные при решении числовых выражений числа в порядке убывания и прочитайте, о чём мы будем сегодня говорить. Запишите этот ряд в тетрадях в строчку, через запятую.
Учитель: О чём мы будем сегодня говорить?
Дети: О задачах.
(На доске открывается часть темы.)
б) повторение изученного о задачах
Учитель: А теперь определим, что нового мы сегодня узнаем о задачах.
(На доске вывешивается схема краткой записи задачи на нахождение суммы.)
Учитель: Что можете сказать об этой задаче по схеме краткой записи.
Дети: Это задача на нахождение суммы.
Учитель: Сколько вопросов в этой задаче? Какой?
Дети: Один. Сколько всего? или Сколько вместе?
Учитель: Какая схема-модель подходит к этой задаче?
(Из схем-моделей выбирают.)
Учитель: Какое буквенное выражение подходит к решению этой задачи.
(Из буквенных выражений на доске дети выбирают: а + в.)
Учитель: Составьте подобную задачу.
(Дети предлагают свои варианты.)
(На доске вывешивается схема краткой записи задачи на уменьшение числа на несколько единиц.)
Учитель: Что можете сказать об этой задаче?
Дети: Это задача на уменьшение числа на несколько единиц.
Учитель: Сколько вопросов в этой задаче? Какой?
Дети: Один. Сколько единиц во второй части.
Учитель: Какая схема-модель подходит к этой задаче?
(Из схем-моделей выбирают.)
Учитель: Какое буквенное выражение подходит к решению этой задачи.
(Из буквенных выражений на доске дети выбирают: а – в.)
(На доске вывешивается схема краткой записи задачи на увеличение числа на несколько единиц.)
Учитель: Что можете сказать об этой задаче?
Дети: Это задача на увеличение числа на несколько единиц.
Учитель: Сколько вопросов в этой задаче? Какой?
Дети: Один. Сколько единиц во второй части.
Учитель: Какая схема-модель подходит к этой задаче?
(Из схем-моделей выбирают.)
Учитель: Какое буквенное выражение подходит к решению этой задачи.
(Из буквенных выражений на доске дети выбирают: а + в.)
Учитель: А теперь прочитайте выделенные задачи в учебнике на стр.54. Какая схема условия и схема-модель подходит к первой задаче? Почему?
Дети: На уменьшение числа на несколько единиц. Потому, что там сказано «на 5 флажков меньше».
Учитель: Какая схема условия и схема-модель подходит ко второй задаче? Почему?
Дети: На увеличение числа на несколько единиц. Потому, что там сказано «на 5 флажков больше».
III. Постановка учебной задачи
(На доске вывешивается схема краткой записи составной задачи на уменьшение числа на несколько единиц и на нахождение суммы.)
Учитель: Что можете сказать об этой задаче по схеме краткой записи.
(Дети в замешательстве.)
Учитель: Что вас смутило? Сколько вопросов в этой задаче? Какие?
Дети: В этой задаче два вопроса. Первый – сколько единиц во второй части, второй – сколько всего.
Учитель: Из каких двух задач составили эту задачу?
(Дети показывают схемы краткой записи задачи на уменьшение числа на несколько единиц и на нахождение суммы.)
Учитель: Эту задачу составили из двух простых задач. Догадайтесь, как называются такие задачи?
(Дети догадываются: составные задачи.)
Учитель: Вот мы и выяснили тему урока: Составные задачи. Попробуйте сформулировать теперь цели урока: что нового узнаем, чему мы сегодня будем учиться?
(На доске появляются вспомогательные слова:
Учитель: Узнаем, что такое составная задача, научимся отличать составные задачи от простых; будем учиться записывать условие составной задачи; решать составные задачи.
IV. «Открытие» нового знания
а) анализ и краткая запись условия задачи
Уч.стр.55 №140
Учитель: Прочитаем текст первого абзаца. Нужно ли выполнять арифметическое действие, чтобы ответить на поставленный вопрос? Почему?
Дети: Нет. Мы можем ответить без выполнения арифметических действий: если у Миши на 8 марок меньше, то у Коли на 8 марок больше.
Учитель: Поставьте к данному условию вопросы, на которые вы сможете ответить, выполнив арифметические действия.
Дети: Сколько марок у Миши? Сколько марок у обоих мальчиков?
Учитель: Посмотрите как записала решение Маша и скажите, какой вопрос она поставила к условию?
Дети: Сколько марок у Миши.
Учитель: Почему вы так считаете?
Дети: У Миши на 8 меньше, значит могло быть столько же, но без 8.
Учитель: А какой вопрос задал Миша?
(Дети находятся в замешательстве.)
Учитель: Очевидно, Миша поставил такой вопрос, на который не ответишь, выполнив только одно действие. Поэтому в его записи показано, что он выполнил сначала одно действие – 1), а потом второе – 2).
На доске записано:
1) 38 – 8 = 30(м.)
2) 38 + 30 = 68 (м.)
Учитель: Что Миша узнал, выполнив первое действие?
Дети: Сколько марок у Миши.
Учитель: Какой это вид задач?
Дети: На уменьшение числа на несколько единиц.
(На доске вывешивается схема-модель задачи на уменьшение числа на несколько единиц.)
Учитель: Что Миша находит вторым действием?
Дети: Сколько марок всего у Коли и у Миши.
Учитель: Какой это вид задач?
Дети: На нахождение суммы.
Учитель: Какой же главный вопрос задавал Миша к условию задачи?
Дети: Сколько всего марок у мальчиков.
Учитель: Какой ответ в этой задаче?
Дети: Всего 68 марок.
Учитель: Какую задачу получил Миша?
Дети: Миша получил составную задачу.
V. Первичное закрепление
Учитель: Запишем условие и решение следующей задачи. Прочитайте текст задачи.
Чем эта задача отличается от предыдущей?
Дети: Количеством марок у мальчиков. У Миши теперь марок больше.
Записывает на доске один из обучающихся.
а) краткая запись условия задачи
Учитель: О чём задача?
Дети: О марках.
Учитель: Какие главные слова выделим для записи условия?
Дети: «У Коли» и «У Миши».
Учитель: Знаем ли сколько марок у Коли?
Дети: Да, 3 марки.
Учитель: Запишем. Знаем ли сколько марок у Миши? Как это покажем?
Дети: Нет. Поставим знак вопроса.
Учитель: Что нам известно о количестве Мишиных марок? Как это покажем?
Дети: Их на 2 больше. Запишем после вопроса эту подсказку.
Учитель: Прочитайте вопрос задачи.
Дети: Сколько марок у Коли и у Миши вместе?
Учитель: Как покажем это в условии?
Дети: Фигурной скобкой со знаком вопроса.
б) составление схемы-модели
Учитель: Построим схему-модель. Как покажем Колины и Мишины марки?
Дети: Двумя отрезками.
Учитель: Какой отрезок будет больше? Почему?
Дети: Второй. Потому, что у Миши марок больше на 2
Учитель: Обозначьте отрезки данными.
(Дети обозначают.)
Учитель: Как покажем главный вопрос задачи?
Дети: Фигурной скобкой.
Учитель: Сколько вопросов в задаче?
Дети: Два.
Учитель: Какой вопрос главный?
Дети: Сколько всего марок у мальчиков.
Учитель: Как найти сколько всего?
Дети: Надо к Колиным маркам прибавить Мишины марки?
Учитель: Можем ли сразу выполнить это действие? Почему?
Дети: Нет. Мы не знаем сколько марок у Миши.
Учитель: Как найти сколько марок у Миши? Почему?
Дети: К 3 прибавить 2. Потому, что у Миши на 2 марки больше, а у Коли 3 марки.
Учитель: Сколько действий в решении задачи?
Дети: Два.
Учитель: Что найдём первым действием?
Дети: Сколько марок у Миши.
Учитель: Запишем первое действие. Что найдём вторым действием?
Дети: Сколько марок всего у мальчиков.
Учитель: Запишем второе действие.
1) 3 + 2 = 5 (м.) – у Миши.
2) 3 + 5 = 8 (м.)
Учитель: Как запишем ответ задачи?
Дети: Ответ: всего 8 марок.
Учитель: Запишем ответ.
VI. Включение в систему знаний
(Вывешивается схема-модель составной задачи на увеличения числа на несколько единиц и нахождение суммы)
Учитель: Давайте попробуем составить буквенное выражение к этой задаче по схеме-модели. Каков главный вопрос задачи?
Дети: Сколько всего.
Учитель: Как ответить на главный вопрос задачи?
Дети: К первой части прибавить вторую.
(На доске учитель пишет: «I + II»)
Учитель: Первая часть известна?
Дети: Да – а.
(На доске: «I + II»)
а
Учитель: Вторая часть известна?
Дети: Нет.
Учитель: Что сказано о второй части?
Дети: Она на в меньше.
Учитель: Каким буквенным выражением можем это показать?
Дети: а + в.
(На доске: « I + II »)
а а + в.
Учитель: Какое выражение мы получили?
Дети: а + (а + в).
VII. Итог урока, рефлексия
Учитель: С каким понятием мы сегодня познакомились?
Дети: Составные задачи.
Учитель: Посмотрите на задачи, которые мы сегодня ставили перед собой на уроке. Достигли ли мы этих целей?
Дети: Да.
Учитель: Что на уроке у вас получилось особенно хорошо? Проанализируйте свою работу на уроке и оцените её на шкале.
(Дети оценивают свою работу.)
Учитель: На следующем уроке мы продолжим знакомство с составными задачами и узнаем об особой записи хода рассуждений при решении задач, которая называется «дерево-рассуждений».