Приемы учебной работы при обучении решению задач на доказательство
Разделы: Математика
Обучение доказательствам – одна из важнейших целей обучения математике.
Именно при выполнении доказательств оттачивается логическое мышление учеников, разрабатываются логические схемы решения задач, возникает потребность учащихся в обосновании математических фактов.
Начиная изучать геометрию, учащиеся способны осознать необходимость доказательства, однако осуществлению доказательства им только предстоит научиться.
С задачами на доказательство учащиеся встречаются при изучении второй темы курса геометрии 7-го класса “Треугольники”. Опыт проведения доказательств отсутствует. Учащиеся не владеют геометрическим языком, многие не понимают смысла слова “доказать”, поэтому испытывают большие трудности. Я решаю эту проблему, предоставляя учащимся образцы (алгоритмы) доказательства. В ходе изучения теоретического материала вместе с учениками составляем алгоритмы решения задач каждого вида и красочно оформляем их в виде книжки.
Эта книга помогает учащимся в затруднительных случаях быстро найти сходную задачу, вспомнить алгоритм решения, составить план решения.
Обучение решению задач веду постепенно.
7-й класс
Тема “Параллельные прямые”
1.Алгоритм решение задачи: доказать, что прямая … параллельна прямой ….
Тема “Прямоугольный треугольник”
1.Алгоритм решение задачи: доказать, что прямоугольные треугольники … равны
8-й класс
Тема “Параллелограмм”.
1.Алгоритм решение задачи: доказать, что четырехугольник…. будет параллелограммом.
Тема “Подобие треугольников”.
1.Алгоритм решение задачи: доказать, что треугольник …. подобен треугольнику…
Принцип пошаговости формирует навыки решения задач и навыки построения логических цепочек доказательства.
Решение задач учу начинать с предложения “Чтобы доказать, что …”. Ученик называет то, что требуется доказать в конкретной задаче и ведет доказательство по соответствующему алгоритму. Такой ход решения позволяет учащимся понимать смысл поставленной задачи, выстраивать аргументацию, формирует умение анализировать, развивает логическое мышление.
Работая в дальнейшем по модели, ученик на каждом шагу контролирует свои действия, обращаясь к выведенному алгоритму. На любом этапе работы ученик может по сигналу учителя передать “эстафету” решения любому ученику. Этим достигается предельное внимание при решении задачи.
Красочно оформленные алгоритмы учащиеся запоминают быстро. И к концу изучения темы “Признаки равенства треугольников” многие учащиеся хорошо проводят доказательные рассуждения, точно и грамотно выражают свои мысли. Данные алгоритмы учащиеся применяют и при доказательстве теорем.
Разработанные алгоритмы позволили логически упорядочить материал, дать его компактное и наглядное изложение. Они способствуют как подсознательному запоминанию, так и осознанному усвоению материала. При пользовании алгоритмами учащиеся лучше осмысливают, осознают логические взаимосвязи. Это помогает им научиться решать задачи.
Пример решения задачи учениками 7-го класса по теме
“Признаки равенства треугольников”
Доказать BD – биссектриса 
(Устно). Чтобы доказать, что BD биссектриса, нужно доказать, что угол ABD равен углу DBC.Чтобы доказать, что два угла равны, нужно доказать, что равны треугольники, содержащие эти углы
Работа в тетради. Рассмотрим 

(Устно) Чтобы доказать, что два треугольника равны, найдем у них три равных элемента.
АВ = ВС по условию задачи,
АD = DC по условию задачи,
Значит 

В равных треугольниках соответственные элементы равны.
Значит, угол ABD равен углу DBC.
Следовательно, BD-биссектриса по определению биссектрисы угла.
Алгоритмы решения задач на доказательство.
Задача на доказательство – это утверждение, которое необходимо доказать с помощью аксиом и теорем.
Доказательство ведется на основе признаков равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Алгоритм решения задачи: доказать, что отрезок … равен отрезку ….
В равных треугольниках соответственные элементы равны.
Математика
Аксиома есть очевидная истина, не требующая доказательства.
Теорема или предложение есть истина, требующая доказательства.
Доказательство есть совокупность рассуждений, делающих данное предложение очевидным.
Доказательство достигает своей цели, когда при помощи его обнаруживается, что данное предложение есть необходимое следствие аксиом или какого-нибудь другого предложения, уже доказанного.
Всякое доказательство основано на том начале, что при правильном умозаключении из истинного предложения нельзя вывести ложного заключения.
Состав теоремы. Всякая теорема состоит из двух частей, a) условия и b) заключения или следствия.
Условие иногда называют предположением. Оно дано и поэтому иногда получает название данного.
Обратная теорема. Предложение, у которого заключение данной теоремы делается условием, а условие заключением, называется теоремой обратной данной.
В таком случае данная теорема называется прямой.
Две теоремы в совокупности, прямая и обратная, называются взаимно-обратными теоремами.
Они находятся в таком взаимном отношении, что, выбрав любую из них за прямую, можно другую принять за обратную.
В двух взаимно-обратных предложениях одно из них вытекает как необходимое следствие другого.
Если в теореме мы обозначим условие буквой, стоящей на первом месте, а заключение буквой, стоящей на втором месте, то прямую теорему можно схематически представить выражением (Aa), а обратную выражением (aA).
Выражение (Aa) схематически представляет предложение: если имеет место A, то имеет место a.
Если для данного предложения (Aa) имеет место и теорема (aA), то обе теоремы (Aa) и (aA) называются взаимно-обратными теоремами.
Примером двух таких взаимно-обратных теорем могут послужить теоремы:
Первая теорема. В треугольнике против равных сторон лежат равные углы.
Вторая теорема. В треугольнике против равных углов лежат равные стороны.
В первой теореме данным условием будет равенство сторон треугольника, а заключением равенство противолежащих углов, а во второй наоборот.
Не всякая теорема имеет свою обратную.
Примером арифметического предложения, не имеющего своего обратного, может послужить следующая теорема. Если в двух произведениях множители равны, то и произведения равны.
Обратное предположение несправедливо. Действительно, из того, что произведения равны, не следует, что множители равны.
Примером геометрического предложения, для которого обратное предложение не имеет места, может послужить теорема: во всяком квадрате диагонали равны.
Предложение обратное этому будет: если диагонали четырехугольника равны, то он будет квадратом.
Это предположение неверно, ибо диагонали бывают равными не в одном квадрате.
Так как обратное предположение не всегда справедливо, то каждый раз обратное предложение требует особого доказательства.
В теории геометрических доказательств весьма важно иногда знать, когда данное предложение допускает свое обратное.
Для этой цели может послужить следующее правило обратимости. Когда в предположении всем возможным и различным условиям соответствуют все возможные и различные заключения, обратное предложение имеет место.
Рассмотрим для примера.
Прямое предложение. Если два треугольника имеют по две равные стороны, то третья сторона будет больше, равна или меньше третьей стороны другого треугольника, смотря по тому, будет ли угол между равными сторонами больше, равен или меньше соответствующего угла другого треугольника.
В этом предложении трем различным и возможным предположениям об угле соответствуют три различных и возможных заключения о противолежащей стороне, поэтому, согласно с правилом обратимости, данная теорема допускает обратное предположение:
Когда два треугольника имеют по две равных стороны, угол между ними будет больше, равен или меньше соответствующего угла другого треугольника, смотря по тому, будет ли третья сторона больше, равна или меньше третьей стороны данного треугольника.
Кроме обратной прямая теорема может иметь свою противоположную.
Противоположная теорема есть такая, в которой из отрицания условия вытекает отрицание заключения.
Противоположная теорема может иметь свою обратную.
Чтобы обобщить все эти теоремы, мы их представим схематически в следующей общей форме:
Прямая или основная теорема. Если имеет место условие или свойство A, то имеет место заключение или свойство B.
Обратная. Если имеет место B, то имеет место A.
Противоположная. Если не имеет места A, то не имеет места B.
Обратная противоположной. Если не имеет места B, то не имеет места A.
Следующие примеры поясняют на частных случаях взаимное отношение этих теорем:
Прямая теорема. Если при пересечении двух данных прямых третьей соответственные углы равны, то данные прямые параллельны.
Обратная теорема. Если две прямые параллельны, то при пересечении их третье, соответственные углы равны.
Противоположная. Если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
Обратная противоположной. Если прямые не параллельны, соответственные углы не равны.
При геометрическом изложении теорем достаточно доказать только две из этих трех теорем, тогда остальные две теоремы справедливы без доказательства.
На этой связи теорем основан прием, по которому для доказательства обратной теоремы ограничиваются часто только доказательством теоремы противоположной.
Способы геометрических доказательств
Для доказательства геометрических теорем существует два основных способа: синтетический и аналитический.
Эти методы называют иногда сокращенно синтезом и анализом.
Синтез есть такой метод доказательства, в котором данное предложение является необходимым следствием другого, уже доказанного.
В синтезе цепь доказательств начинается с какого-нибудь известного предложения и оканчивается данным предложением. При доказательстве исходное предложение сопоставляется с аксиомой или с другим уже известным предложением. Синтетический способ удобен для вывода таких новых предложений, которые заранее не обозначены. Для доказательства же данного предложения он представляет много неудобств. В нем не видно: a) какую из известных теорем нужно выбрать для того, чтобы доказываемое предложение вытекало как ее необходимое следствие, и b) какое из следствий выбранного предложения приводит к доказываемому предложению.
Синтез называют поэтому не методом открытия новых истин, а методом их изложения.
Впрочем и при самом изложении теорем методом синтетическим является неудобство в том отношении, что не видно, почему за исходную истину в цепи доказательств выбрано то, а не другое предложение, то, а не другое его следствие.
Примером синтетического способа доказательства может послужить следующая теорема.
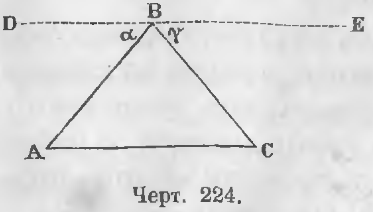
Теорема. Сумма углов треугольника равна двум прямым.
Дан треугольник ABC (черт. 224).
Требуется доказать, что A + B + C = 2d.
Доказательство. Проведем прямую DE параллельную AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно,
то, заменяя в предыдущем равенстве углы α и γ равными им углами, имеем:
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, лежащих по одну сторону прямой.
Она поставлена в связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною.
Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Анализ есть способ обратный синтезу. В анализе цепь рассуждений начинается доказываемой теоремой и оканчивается какой-нибудь другой уже известной истиной.
Анализ является в двух видах. От доказываемого предложения мы можем перейти к предложению, служащему его ближайшим основанием или его ближайшим следствием.
Переходя от данного предложения к предложению, служащему его ближайшим основанием, мы смотрим на данное предложение как на необходимое следствие.
Переходя от данного предложения к его ближайшему следствию, мы смотрим на данное предложение как на основание для цепи умозаключений.
Первый способ анализа. Совершая анализ переходом к основанию, отыскивают то первое ближайшее предложение, из которого данное вытекает как необходимое следствие. Если это предложение было прежде доказано, то доказано и данное предложение, если же нет, то отыскивают второе предложение, служащее основанием для первого.
Такой переход к основанию следует продолжать до тех пор, пока не дойдем до предложения вполне доказанного. Данное предложение явится как необходимое следствие последнего доказанного предложения.
Обозначая каждое предложение буквой и ставя ее впереди или позади другой, смотря по тому, будет ли оно служить основанием или следствием другого предложения, мы схематически можем этот прием анализа выразить в виде
где M есть данное предложение, L его ближайшее основание, а H предложение, вполне доказанное. Если верно предложение H, то верно предложение K; если верно K, то верно L; если верно L, то верно и M.
Второй способ анализа состоит в переходе от данного предложения к его следствию. Этот прием применяют чаще, потому что легче находить необходимое следствие, нежели отыскивать основание какой-нибудь истины. По этому способу выводят из данного предложения ту теорему, которая служит его ближайшим следствием. Если это следствие есть предложение прежде доказанное, то на нем и останавливаются; если же нет, переходят к следующему ближайшему следствию и вообще продолжают такой последовательный вывод следствий до тех пор, пока не дойдут до предложения, вполне доказанного.
Если последнее предложение не верно, то и данное не верно, ибо неверное следствие нельзя получить из верного предложения.
Если же последнее предложение верно, то для убеждения в верности данного предложения требуется, чтобы были соблюдены некоторые условия.
Схематически этот прием анализа можно представить в виде
M — N — O — P — Q — R — S
где M данное предложение, N предложение, служащее его ближайшим следствием, а S то последнее предложение, в справедливости которого мы вполне убеждены.
Из двух предложений R и S, стоящих в такой связи, что если справедливо R, то справедливо и предложение S, мы, как известно, не всегда можем обратно заключать, что если справедливо S, то справедливо и предложение R.
Чтобы последнее заключение имело место, требуется, чтобы теоремы R и S были взаимно-обратными предложениями.
Итак, для того, чтобы убедиться, что теоремы R и S стоят в такой связи, что она удовлетворяет схеме R — S и схеме S — R, требуется доказать, что предложения R и S взаимно-обратны.
Таким образом, чтобы можно было по верности последнего предложения S заключить о верности данного предложения M, требуется доказать, что каждые два рядом стоящие предложения R и S, P и R, O и P, N и O, M и N удовлетворяют закону обратимости.
Если это доказано, то цепь предложений можно обратить, и рядом со схемой M — N — O — P — Q — R — S справедлива и схема
S — R — Q — P — O — N — M
по которой мы имеем право заключить, что если справедливо предложение S, то справедливо и предложение M.
Так как затруднительно всякий раз доказывать обратимость двух предложений, то этого избегают, соединяя способ аналитический с синтетическим. После того, как из предложения M выведено предложение S как его следствие, смотрят, нельзя ли обратно вывести предложение M как необходимое следствие предложения S.
Если синтез есть способ, называемый дедукцией или выводом, то анализ можно назвать редукцией (приведение, наводка).
Примером аналитического способа доказательства может послужить следующая теорема.
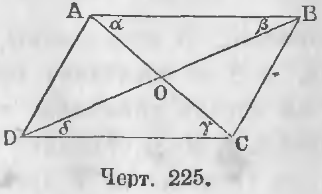
Теорема. Диагонали параллелограмма пересекаются пополам.
Доказательство. Если диагонали пересекаются пополам, то треугольники AOB и DOC равны (черт. 225). Равенство же треугольников AOB и DOC вытекает из того, что AB = CD как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до предложения уже доказанного.
Сравнение синтеза с анализом. Способ аналитический вернее ведет к доказательству данной теоремы, ибо от данной теоремы легче переходить к его ближайшему основанию или следствию.
Хотя анализ лучше синтеза объясняет, почему выбран тот или другой путь для доказательства теоремы, однако неопределенность при доказательствах не устраняется вполне в том смысле, что при последовательных заменах одного предложения другим, мы не всегда можем дойти до предложения нам известного, ибо иногда не видно, какое из следствий или какое из оснований данного предложения нужно выбрать для того, чтобы его доказать. Затруднения увеличиваются еще больше, когда приходится для доказательства проводить новые вспомогательные прямые. Иногда трудно дать верные указания, какие из них облегчают доказательство данной теоремы.
Анализ, как и все логические приемы, только облегчает и помогает находить доказательство данного предложения, но не всегда необходимо ведет к самому доказательству.
Кроме этих прямых существует непрямой способ доказательства, известный под именем доказательства от противного или способа приведения к нелепости.
Способ доказательства от противного состоит в том, что для доказательства данного предложения убеждают в невозможности предположения противоположного.
На этом основании это доказательство называется доказательством от противного. Оно достигает своей цели всякий раз, когда из двух предложений, данного и противоположного, одно непременно имеет место.
В этом случае для доказательства данного, допустив противоположное предложение, выводят из него такие следствия, которые противоречат аксиомам или теоремам, уже доказанным. Если одно из следствий этого предложения ложно, то и противоположное предложение ложно, а следовательно данное предложение справедливо.
Этот прием часто применяют для доказательства теорем обратных или противоположных данным.
Не трудно заметить, что этот способ есть второй способ анализа, в котором от данного предложения последовательно переходят к его следствиям.
Примером применения такого способа может послужить приведенное выше доказательство теоремы: против равных углов в треугольнике лежат равные стороны (теорема 26).
В геометрии также применяют способы, зависящие от самого содержания геометрических истин. Геометрические истины относятся к геометрическим протяжениям. Эти протяжения обладают определенными свойствами, подлежащим внешним чувствам. Геометрическое протяжение может рассматриваться как целое, доступное наблюдению внешними чувствами. Убедительности доказательства содействует и самое чувственное созерцание. Обойтись без него в геометрии невозможно.
К числу приемов, имеющих место в геометрии, принадлежат: способ наложения, способ пропорциональности и способ пределов.
Способ наложения состоит в том, что одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений, смотря по тому, совмещаются или не совмещаются ни при наложении.
Способ пропорциональности состоит в применении к геометрическим протяжениям свойств пропорций. Этот способ применяется при доказательстве теорем, относящихся к подобным фигурам и к пропорциональным отрезкам.
Способ пределов состоит в том, что вместо данных протяжений рассматривают свойства протяжений близких по своим свойствам к данному, и выводы, получаемые из рассмотрения одних, применяют к другим сходным протяжениям.
Способы решения геометрических задач
При решении геометрических задач синтез и анализ применяют точно так же как и при доказательстве теорем.
Решая задачу синтетически, берут такую другую задачу, которую умеют решить, потом из ее решения выводят решение следующей задачи, как ее необходимое следствие, и поступают так до тех пор, пока не доходят до решения данной задачи.
Синтетический метод решения задачи обладает всеми теми же недостатками, какими обладает и синтетический метод доказательства.
Поэтому чаще и успешнее для решения задач применяют анализ.
При решении задачи анализом заменяют данную задачу новой. Эту новую задачу будем называть заменяющей.
Если две задачи находятся в таком отношении, что условия второй есть необходимые следствия условий первой, то первую задачу будем называть начальной, а вторую — производной.
При анализе существуют два способа.
Первый способ. Заменяющую задачу выбирают так, чтобы условия данной задачи вытекали как необходимое следствие условий новой заменяющей задачи, т. е. по нашей терминологии от данной задачи переходят к первой начальной задаче. Если решение этой задачи известно, то решение данной является как необходимое следствие решения начальной задачи. Если же ее решение неизвестно, то от нее переходят ко второй, третьей начальной задаче и продолжают так поступать до тех пор, пока не получат задачу, решение которой известно.
Решив эту последнюю задачу, вместе с этим последовательно доходят и до решения данной задачи.
Второй способ. Можно переходить от данной задачи к такой другой, условия которой являются следствием условий данной, т. е. от данной задачи переходят к ее производной.
Заменяя таким образом последовательно одну задачу другой ее производной, мы можем дойти до задачи, решение которой уже известно. Решение этой задачи дает иногда возможность решить и данную задачу.
Такой переход от данной задачи к ее производной применяют чаще, ибо переходить к следствию легче, нежели подыскивать основание для какой-нибудь истины.
В этом частном случае анализа обыкновенно полагают, что задача решена, и из этого предположения выводят соотношения, дающие возможность решить данную задачу.
При переходе от данной задачи к ее заменяющей весьма важно обращать внимание на то, будут ли две задачи обладать свойством взаимной обратимости. Эта взаимность в условиях двух задач является тогда, когда одна задача, будучи начальной для другой, может быть в то же время и ее производной; иначе когда две задачи находятся в таком отношении, что условия одной могут быть и необходимыми следствиями другой и наоборот.
Если две задачи, данная и новая, обладают такими свойствами, то новая задача вполне заменяет данную. В этом случае все решения одной будут и решениями другой.
Если же условия двух задач не обладают свойствами взаимной обратимости, то, заменяя данную задачу новой, мы можем найти или лишние решения или иметь некоторые из решений потерянными.
Если заменяющая задача будет производной для данной, то мы можем найти некоторые лишние решения; если же она будет начальной для данной, то мы можем найти некоторые решения потерянными.
Так как чаще от данной задачи переходят к задаче производной, то чаще приходится получать решения лишние.
Чтобы отделить лишние решения и отыскать потерянные, поверяют все найденные решения.
Поверка есть способ отделения посторонних (лишних) решений. Она дополняет анализ.
Аналитическое решение задачи указывает на то построение, которое нужно сделать для решения задачи. Совершая это построение, поступают при решении задачи способом обратным анализу, т. е. прибегают к синтетическому способу. Этот синтетический способ часто может заменить и самую поверку найденных решений.
Совместное применение синтеза и анализа дает средство избегнуть тех ошибок, которые могут получиться при применении только одного из этих методов решения.
Решим одну и ту же задачу синтетически и аналитически. Для примера может послужить следующая задача.
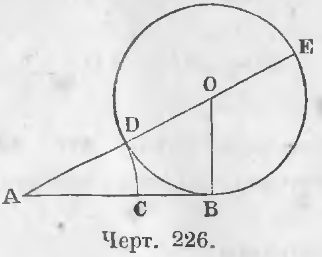
Задача. Разделить данный отрезок AB в крайнем и среднем отношении.
Решение. Восставим из конца отрезка AB перпендикуляр BO равный половине AB (черт. 226). Из центра O опишем окружность радиусом BO, соединим центр O с точкой A и отложим на отрезке AB отрезок AC равный AD, тогда отрезок AC или AD будет искомый.
Доказательство. Прямая AB — касательная к окружности, следовательно
Так как DE = AB и AD = AC, то в предыдущей пропорции имеем:
откуда имеем пропорцию
Это решение синтетическое. В нем мы отправляемся от известной теоремы о свойствах касательной и решение данной задачи вытекало как необходимое следствие этой теоремы.
Решение аналитическое. Допустим, что задача решена, а следовательно и отрезок AC найден, тогда
(AB + AC)/AB = (AC + CB)/AC
Из последней пропорции видно, что AB есть касательная, AB + AC пересекающаяся, AC ее внешний и AB внутренний отрезок.
Отсюда вытекает и само построение. Нужно из конца B восставить перпендикуляр равный ½AB, провести окружность, соединить O с A и отложить на отрезке AB часть AC = AD.
В этом аналитическом решении мы данную задачу, удовлетворяющую условию (1), заменяем задачей, удовлетворяющей условию (2).
Условие (2) указывает и путь для решения самой задачи построением.
Обыкновенно, найдя решение задачи способом аналитическим, совершают построение, в котором, применяя способ рассуждений синтетический, доказывают, что это построение действительно разрешает задачу и этим доказательством заменяют поверку, имеющую в виду устранить посторонние решения.
В данном примере между задачами, удовлетворяющим условиям (1) и (2), существует полная обратимость, ибо из условий (1) вытекают условия (2) как необходимое следствие и наоборот, поэтому здесь нет ни потерянных, ни посторонних решений.
Исследование второстепенных и вспомогательных приемов решения задач еще не достигло в своей обработке полной и совершенной законченности. Мы пока устраняемся от их подробного рассмотрения.