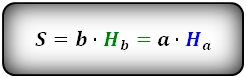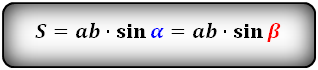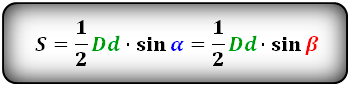Параллелограмм
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
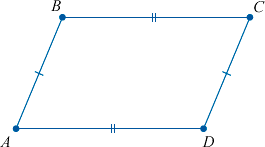
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Теорема (второй признак параллелограмма)
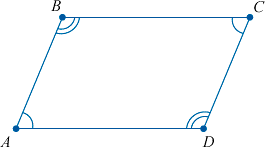
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Теорема (третий признак параллелограмма)
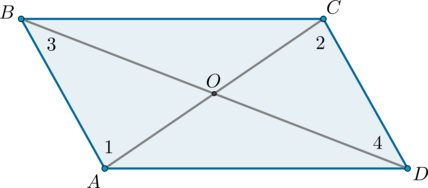
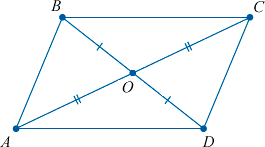
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
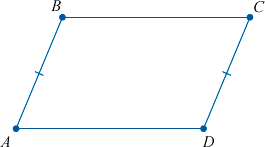
Итак, в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник \(ABCD\) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
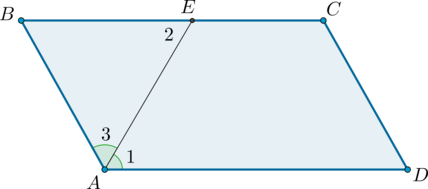
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
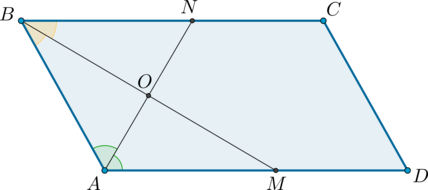
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
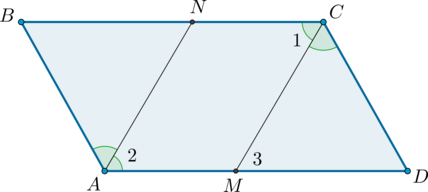
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
2) Пусть \(ABCD\) – параллелограмм, \(AN\) и \(BM\) – биссектрисы углов \(BAD\) и \(ABC\) соответственно.
Как правильно сокращать слова
При написании текстов рано или поздно каждый копирайтер сталкивается с сокращениями. Тогда возникают вопросы: как правильно сократить слово, можно ли его сокращать вообще, на какие правила ориентироваться при сокращении. Хорошо, если автор начинает задумываться над, казалось бы, такими незначительными моментами. Ведь любая неточность в тексте, опечатка или ошибка могут вызывать эффект отторжения у грамотного человека, разрушить атмосферу, которую вы пытаетесь создать.
Сегодня постараемся затронуть все вопросы, которые могут появиться при написании текстов для продажи товара, услуги. Также эта статья будет полезна для авторов блогов, администраторов сайтов, страниц социальных сетей и всех, кто желает разобраться в непростой теме сокращений слов.
Какими правилами руководствуемся
В первую очередь нужно сказать, что при написании любого текста (даже сообщения в мессенджере) следует ориентироваться на адресата. Если пишется сообщение другу, то, конечно, соблюдать общепринятые правила или нет — полностью решение автора. В SMS «и так далее» можно заметить «и тэдэ», а «килограмм» на «кэгэ», и никто не задаст вопроса об уместности такого сокращения. Допустимо ли оно при написании официального письма, статьи на сайт, при заполнении документов? Нет, нужно придерживаться правил.
Основные правила сокращения слов в русском языке
В любом информационном тексте, который предназначен для прочтения даже небольшой аудиторией, допускаются лишь общепринятые сокращения, понятные без расшифровок.
Основные правила сокращения:
Как сокращать существительные во множественном числе
Обратите внимание, что года, века, тысячелетия, а также любые числовые значения пишутся через тире (а не дефис) и без пробелов.
Частные случаи сокращений
Ниже рассмотрим варианты сокращения слов в русском языке, вопросы о правильности которых появляются особенно часто.
Как правильно сократить почтовые сведения
Сократить слово «район» можно только как « р-н» (без точки) и никак иначе.
Как правильно сокращать единицы измерения
При написании текстов на страницы товаров часто нужно указывать их размеры, мощность, массу. Единицы измерения пишут полностью редко, поскольку это не только не принято, но и отвлекает внимание от параметров. Чаще всего после единицы измерения точки не ставят: ее написание считается грубым нарушением правил. Однако здесь есть исключения. Рассмотрим основные сокращения.
| Измерение массы | |
| грамм | г (никаких гр.) |
| килограмм | кг |
| центнер | ц |
| тонна | т |
| Измерение времени | |
| секунда | с |
| минута | мин. мин (при написании текстов по ГОСТу) |
| час | ч. ч (при написании текстов по ГОСТу) |
| Измерение длины (расстояния) | |
| миллиметр | мм |
| сантиметр | см |
| дециметр | дм |
| метр | м |
| километр | км |
Другие единицы измерения сокращаются таким образом: ампер (А, международное — A), ватт (Вт, международное — W), вольт (В, международное — V).
Сокращение чисел
С. или стр.
Как правильно сократить слово « рубли »
Всем известны сокращения «и др.», «и пр.». Главное правило написания: сокращение ставим после определяемого слова. Так, « также для украшения свадебного зала вы можете приобрести цветы: розы, тюльпаны, хризантемы, ромашки, лилии и др.» — правильно, а «в нашем зоопарке вы сможете познакомиться с обезьянами, львами, тиграми, жирафами, волками и др. животными» — неправильно. В последнем случае возможно лишь полное написание слова.
Аббревиатуры
Часто встречается ошибка при сокращении сочетания «фамилия, имя, отчество». Ф. И. О. — верно, как и написание аббревиатуры строчными буквами ( ф.и.о. ), сокращение ФИО считается неправильным.
Немного о времени
Заключение
В статье были рассмотрены общие правила сокращения слов, а также частные случаи, с которыми чаще всего встречаются копирайтеры при написании текстов. Однако, чтобы полностью осветить тему, понадобилось бы слишком много времени. Поэтому в каждом конкретном случае автору придется углубиться в справочники для грамотного написания сокращений.
Соблюдение этих правил поможет создать приятный и легкий для прочтения текст.
Параллелограмм — это базовая геометрическая фигура с рядом важных свойств и признаков
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
В этой статье мы подробно расскажем о таком термине, как ПАРАЛЛЕЛОГРАММ.
С этой фигурой каждый из нас познакомился еще в школе – на уроках геометрии в 8 классе. Но если кто проболел в то время, прогулял занятия или просто не усвоил материал – мы поможем закрыть этот пробел.
Определение параллелограмма
Параллелограмм – это геометрическая фигура, которая является разновидностью четырехугольника. У него противоположные стороны лежат на параллельных линиях, а соответственно, являются параллельными по отношению друг к другу.
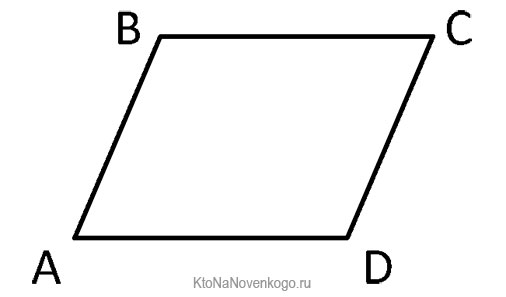
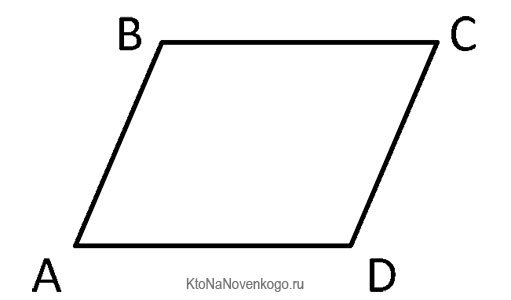
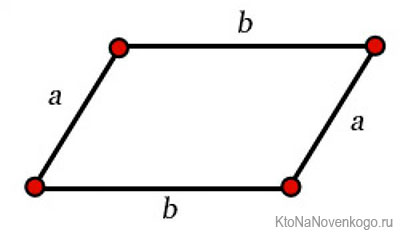
Выглядит эта фигура вот так:
Это классический вид параллелограмма, который в учебниках приводят всегда в первую очередь. В данной фигуре сторона AD параллельна стороне ВС, а АВ параллельна CD.
Интересно, что более известные всем нам фигуры – квадрат, прямоугольник и ромб – также являются параллелограммами.
Можно даже дать такие определения:
Происхождение термина «параллелограмм»
Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАММ пришло к нам из Древней Греции. И легко предположить, что оно как-то связано с самым известным в истории математиком – Евклидом.
Действительно, так и есть. Слово ПАРАЛЛЕЛОГРАММ впервые можно найти именно в трудах Эвклида, которые называются «Начала». Оно состоит из двух греческих слов – «Parallelos», что, естественно, означает «параллельный», и «Gramme» — «линия».
Таким образом, ПАРАЛЛЕЛОГРАММ можно перевести как «параллельные линии». Этот принцип и заложен в определении геометрической фигуры.
Еще любопытный факт, что именно Евклид поделил все четырехугольники на две большие категории. Первая – это параллелограммы, у которых противоположные стороны параллельны. И трапеции (что это?), у которых параллельна только одна пара сторон.
Свойства и признаки параллелограмма
Как понять, что перед нами ПАРАЛЛЕЛОГРАММ? Есть целый ряд признаков, который характерен только для этой геометрической фигуры.
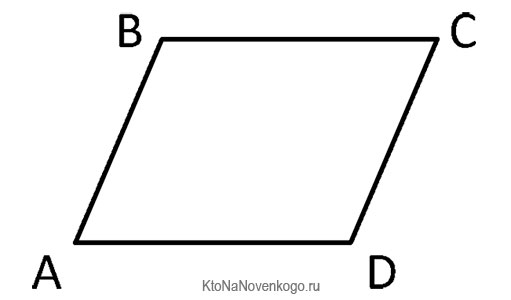
Возьмем в качестве примера еще раз нашу фигуру:
Чтобы этот четырехугольник ABCD можно было считать параллелограммом, должно выполняться одно из следующих условий:
AD II BC и AD =BC. Или AB II CD и AB = CD
∠А + ∠В = ∠В + ∠С = ∠С + ∠D = ∠D + ∠А = 180
Это самые простые признаки параллелограмма. Есть еще некоторые признаки, смысл которых поясняется в этом видео:
Причем, для того чтобы удостовериться в подлинности фигуры, достаточно доказать только одно из них.
Правило действует и в обратную сторону – если хоть один из признаков параллелограмма верен, то автоматически верны и все остальные, и они не нуждаются в отдельном доказательстве.
Соответственно, если хоть один признак не получил подтверждения, то фигуру нельзя считать параллелограммом. И все остальное также не совпадет.
Как посчитать периметр параллелограмма
Для подсчетов длины периметра четырехугольников обычно просто складывают длины его сторон. Но в случае с параллелограммом все несколько проще, так как стороны у него попарно равны.
Снова возьмем для примера нашу фигуру:
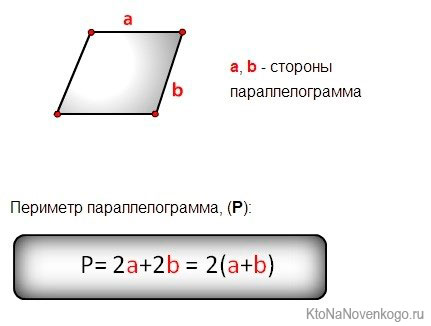
Только для удобства обозначим стороны по-другому. AD и ВС будет просто «а», а АВ и CD – «b». Получится вот так:
Чтобы рассчитать периметр, надо просто сложить все стороны:
Но эту же формулу можно переиначить и по-другому:
Это и есть формула периметра параллелограмма, которая записана во всех учебниках.
Как рассчитать площадь параллелограмма
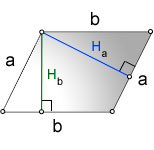
С площадью геометрических фигур всегда чуть сложнее, чем с периметрами. Но параллелограмм в какой-то мере уникален, потому что для расчета его площади существует сразу несколько формул.
Напомним, высотой называют линию, которая выходит из вершины геометрической фигуры и идет под прямым углом к противоположному основанию.
Вот и все, что мы хотели рассказать о ПАРАЛЛЕЛОГРАММЕ. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Сталкивалась с этим словом только в школе, на уроках геометрии, больше нигде ?
Как найти площадь параллелограмма
Онлайн калькулятор
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.
Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):
Подставьте значения в соответствующие поля и получите результат.
Зная длину стороны a и длину высоты h
Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?
Формула
Пример
Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:
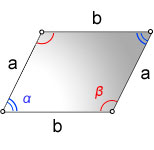
Зная длины сторон a и b, и угол α
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?
Формула
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:
S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см 2
Зная длины сторон a и b, и угол β
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?
Формула
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:
S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см 2
Зная длины сторон a и b, и длину диагонали (d1 или d2)
Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?
Формула
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:
S = 2 √ 12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅ √ 12⋅4⋅7⋅1 = 2⋅ √ 336 = 36.66 см 2
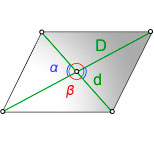
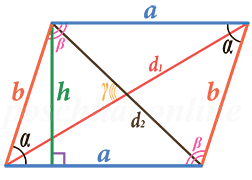
Зная длины диагоналей d1 и d2, и угол между ними γ
Чему равна площадь параллелограмма S если известны длины диагоналей d1 и d2, и угол между ними γ?
Формула
Пример
Если диагональ параллелограмма d1 = 11 см, диагональ d2 = 7 см, а ∠γ = 45° то:
S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см 2
Параллелограмм
Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Содержание
Свойства
пусть а — длина стороны AB, b — длина стороны BC, 


Наконец, углы, прилежащие к одной стороне, например ∠A и ∠D, дают в сумме 180°, так как это углы внутренние односторонние при параллельных прямых.
По теореме косинусов: 


Признаки параллелограмма
Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:
1. Если в четырёхугольнике противоположенные стороны попарно равны, то четырёхугольник параллелограмм 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник параллелограмм 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник параллелограмм
Площадь параллелограмма
См. также
Планигон
Полезное
Смотреть что такое «Параллелограмм» в других словарях:
ПАРАЛЛЕЛОГРАММ — всякий четырехугольник, противоположные стороны которого попарно равны и параллельны; преимуществ. так назыв. удлиненный четырехугольник, с двумя острыми и двумя тупыми углами; прочие же виды параллелогр. имеют свои особ. названия (ромб, квадрат … Словарь иностранных слов русского языка
параллелограмм — а, м. parallélogramme m. <лат. <гр. parallelogrammon. 1. мат. Четвероугольник, у которого все стороны попарно параллельны. БАС 1. Некоего четвероуголия не равнобочнаго именуемаго паралеллеграмма дан диагональ. Арифм. Магн. 214. // Сл. 18 6… … Исторический словарь галлицизмов русского языка
ПАРАЛЛЕЛОГРАММ — (от греч. parallelos параллельный и gramme линия) четырехугольник, у которого стороны попарно параллельны. Частные виды параллелограммов: прямоугольник параллелограмм, все углы которого прямые; ромб параллелограмм, все стороны которого равны;… … Большой Энциклопедический словарь
параллелограмм — прямоугольник, квадрат, ромб, четырехугольник, ромбоид Словарь русских синонимов. параллелограмм сущ. • ромбоид Словарь русских синонимов. Контекст 5.0 Информатик. 2012 … Словарь синонимов
ПАРАЛЛЕЛОГРАММ — ПАРАЛЛЕЛОГРАММ, четырехугольник (четырехсторонняя плоская фигура), у которого каждая пара противоположных сторон параллельна. У параллелограмма противоположные стороны и противоположные углы равны. Площадь параллелограмма равна произведению одной … Научно-технический энциклопедический словарь
ПАРАЛЛЕЛОГРАММ — ПАРАЛЛЕЛОГРАММ, параллелограмма, муж. (от греч. parallelos параллельный и gramma начертание) (мат.). Четыреугольник, противоположные стороны которого равны и параллельны. ❖ Параллелограмм сил или скоростей (геом.) способ нахождения… … Толковый словарь Ушакова
ПАРАЛЛЕЛОГРАММ — ПАРАЛЛЕЛОГРАММ, а, муж. В математике: четырёхугольник, у к рого стороны попарно параллельны. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Параллелограмм — четырехугольник, каждая пара противоположных сторонкоторого параллельны и равны между собой … Энциклопедия Брокгауза и Ефрона
ПАРАЛЛЕЛОГРАММ — плоская четырёхугольная геометрическая фигура, противоположные стороны которой взаимопараллельны. К П. относятся: квадрат, прямоугольник, ромб … Большая политехническая энциклопедия
параллелограмм — а; м. [от греч. parallēlos параллельный и grammē линия] Матем. Четырёхугольник, противоположные стороны которого параллельны. Построить, начертить п. П. сил (спец.; геометрическое построение, выражающее закон сложения сил). * * * параллелограмм… … Энциклопедический словарь