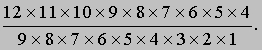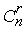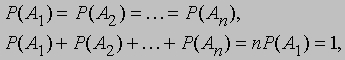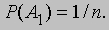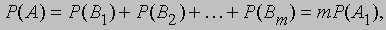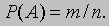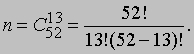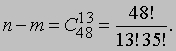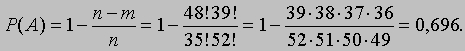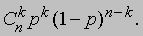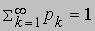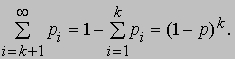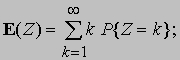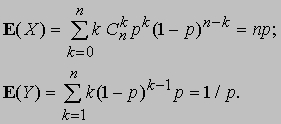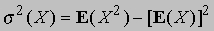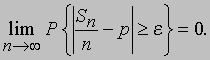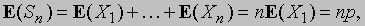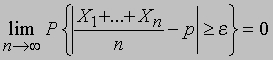«Вероятно». Обособляется или нет?
Слово «вероятно» употребляется как в роли вводного слова, так и члена предложения. В соответствии с его синтаксической ролью, которая обуславливается контекстом, расставляются запятые.
Вводное слово
Вводное слово «вероятно» помогает говорящему выразить оценку степени достоверности сообщаемой информации (предположение, возможность, уверенность и так далее). Используется в значении «по-видимому», «наверно (наверное)», «можно думать», «должно быть».
Оно не является членом предложения, поэтому выделяется запятыми. Вводное слово можно удалить из предложения без нарушения его структуры и потери смысла.
Запятые при вводном слове
Вводное слово «вероятно» выделяется запятыми с двух сторон, если оно находится в середине предложения. При расположении в начале или конце предложения оно отделяется одной запятой.
При встрече двух вводных слов, между ними должна стоять запятая.
Вводное слово обособляется запятыми с двух сторон, если оно находится в середине обособленного члена предложения. В начале или конце обособленного оборота вводное слово не отделяется запятой. В этом случае запятые ставятся лишь по границам оборота.
Если обособленный член предложения заключен в скобки, то вводное слово выделяется запятыми всегда.
Если вводное слово находится перед сравнительным оборотом с союзом «как» или целевым оборотом с союзом «чтобы», то обособляется запятыми, как обычно.
Между сочинительным союзом («а», «и», «но», «да») и вводным словом ставится запятая, если вводное слово можно изъять из предложения или переместить без нарушения его структуры.
Если изъятие вводного слова приводит к нарушению структуры и смысла предложения, то запятая между союзом и вводным словом не ставится.
Запятая между союзом и вводным словом не ставится также, если они находятся в начале предложения.
Однако автор может выделить вводное слово интонацией, поэтому запятая между союзом и вводным словом в начале предложения может присутствовать.
Член предложения
Слово «вероятно» может выступать в роли члена предложения, наречия, краткого прилагательного или предикатива. Выделять запятыми члены предложения не нужно.
Определительное (качественное) наречие «вероятно» отвечает на вопрос «как?» и является обстоятельством в предложении.
Краткое качественное прилагательное «вероятно» отвечает на вопрос «каково?» и выполняет функцию сказуемого.
Иногда «вероятно» выполняет роль предикатива, то есть сказуемого. В этой роли оно дает оценочную характеристику ситуации, чьих-либо предполагаемых действий.
Частица
Иногда слово «вероятно» встречается в роли частицы, которая придает утверждению интонацию неуверенности.
вероятно
Вероятно, лифт сегодня не починят. | Этот метеорит, вероятно, упал на Землю много миллионов лет назад.
Весьма вероятно, что в новой Думе корпус депутатов обновится на две трети. | Вполне вероятно, что к концу сезона цены на этот товар резко упадут.
Ты сможешь приехать к нам на дачу? — Вероятно.
Акции этого предприятия, вероятнее всего, упадут уже к январю.
Смотреть что такое «вероятно» в других словарях:
вероятно — По всей вероятности, по всему вероятию, по всем вероятиям, возможно, верно, может быть, быть может, может статься, надо полагать, надо быть, должно быть, значит, знать, правдоподобно; чай, поди, небось, пожалуй; чего доброго; того и жди, едва ли… … Словарь синонимов
ВЕРОЯТНО — ВЕРОЯТНО, вводное слово (разг.). По видимому, надо полагать, можно думать. В шесть часов я, вероятно, буду дома. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
вероятно не — См … Словарь синонимов
вероятно — вводное слово, в значении сказуемого и частица 1. Вводное слово. То же, что «наверное, должно быть, по видимому». Выделяется знаками препинания, обычно запятыми. Подробно о пунктуации при вводных словах см. в Приложении 2. (↑Приложение 2) Вот… … Словарь-справочник по пунктуации
вероятно — ▲ возможно ↑ какой л. степени вероятно возможно в какой то степени. наверное. наверно. верно. по всей вероятности. по всем вероятиям [вероятностям]. по видимому. видимо. по видимости. очевидно. видно. должно быть. надо думать [полагать]. должно… … Идеографический словарь русского языка
Вероятно — I предик. Оценочная характеристика ситуации, чьих либо действий как возможных, допустимых. II част. 1. Употребляется при выражении неуверенного подтверждения. 2. Употребляется как вводное слово, выражающее возможность или допустимость чего либо и … Современный толковый словарь русского языка Ефремовой
Вероятно — I предик. Оценочная характеристика ситуации, чьих либо действий как возможных, допустимых. II част. 1. Употребляется при выражении неуверенного подтверждения. 2. Употребляется как вводное слово, выражающее возможность или допустимость чего либо и … Современный толковый словарь русского языка Ефремовой
Вероятно — I предик. Оценочная характеристика ситуации, чьих либо действий как возможных, допустимых. II част. 1. Употребляется при выражении неуверенного подтверждения. 2. Употребляется как вводное слово, выражающее возможность или допустимость чего либо и … Современный толковый словарь русского языка Ефремовой
вероятно — веро ятно, вводн. сл … Русский орфографический словарь
вероятно — I. нареч., в функц. сказ. Возможно, допустимо. Вполне в., что ты прав. II. вводн. сл. По видимому, наверно. В., сегодня задержусь. Он, в., занят. III. частица. Выражает не совсем уверенное подтверждение. Вы вернётесь? В. ◁ Вероятнее всего, в зн.… … Энциклопедический словарь
«Вероятнее всего». Запятые ставятся или нет?
Устойчивое выражение «вероятнее всего» («вероятней всего») может выступать в роли вводного словосочетания или члена предложения. Запятые ставятся в зависимости от его роли в контексте предложения.
Вводное словосочетание
Вводное словосочетание «вероятнее всего» используется в значениях: «должно быть», «наверное», «скорее всего».
Вводное словосочетание не имеет ни синтаксических, ни грамматических связей с другими словами в предложении. Оно не отвечает на вопросы, и от него также нельзя сформировать вопрос.
Вводное словосочетание можно переставить или удалить из предложения. При этом смысл и структура высказывания не изменятся. Оно не является членом предложения и обычно обособляется запятыми, за исключением некоторых случаев.
Одиночное вводное словосочетание
Вводное словосочетание отделяется одной запятой, если расположено в начале или конце предложения. В средней части предложения оно обособляется запятыми с двух сторон.
В обособленном обороте
Вводное словосочетание не отделяется запятой в начале или конце обособленного оборота (причастного, деепричастного, уточняющего и т. д.). Запятые ставятся по границам всего оборота.
Вводное словосочетание выделяется запятыми с двух сторон в середине оборота. При этом запятые ставятся также в начале и конце оборота.
Если оборот обособлен при помощи тире или скобок, то вводное словосочетание выделяется запятыми всегда, в любом месте оборота.
С союзом
Между сочинительным союзом («и», «а», «но», «да») и вводным словосочетанием ставится запятая, если вводное словосочетание можно удалить или переместить без потери смысла или нарушения структуры предложения.
Если без вводного словосочетания предложение становится некорректным по смыслу и структуре, то после сочинительного союза запятая не ставится. Они объединяются в единую конструкцию и обособляются вместе.
Не отделяется запятой присоединительный союз от вводного словосочетания в начале предложения.
При интонационном выделении вводного словосочетания, а также при его включении в текст посредством подчинительного союза, между присоединительным союзом и вводным словосочетанием может ставиться запятая.
Вводное словосочетание всегда отделяется запятой от целевого оборота с союзом «чтобы» и сравнительного оборота с союзом «как».
При однородных членах
Если вводное словосочетание разделяет ряд однородных членов и обобщающее слово, то перед вводным словосочетанием ставится тире, а после него — запятая.
В сложном предложении перед тире необходимо поставить еще одну запятую, разделяющую его части.
Если вводное словосочетание находится после обобщающего слова, а за ним следует ряд однородных членов, то перед вводным словосочетанием ставится запятая, а после него — двоеточие.
Вводное словосочетание, расположенное между двумя однородными определениями, может объединяться со вторым определением в уточняющую конструкцию. Первая запятая ставится перед вводным словосочетанием, а вторая — в конце оборота.
В сложном бессоюзном предложении
Иногда становится неясно, к какой именно части бессоюзного сложного предложения или к какому однородному члену относится вводное словосочетание. Если оно связано по смыслу со следующим за ним предложением или словом, то не отделяется от него запятой.
Два вводных слова
Всегда разделяются запятой находящиеся рядом вводные слова или словосочетания.
С усилительной частицей
Не отделяется запятой усилительная частица («ведь», «все-таки», «все», «все же», «даже», уж«, «неужели», «разве» и т. д.) от вводного словосочетания.
Иногда неясно, к какой части сложного предложения относится вводное словосочетание. В этом случае оно обособляется двумя запятыми, а после первой запятой дополнительно ставится тире.
Тире перед вводным словосочетанием также используется, чтобы показать причинно-следственные связи или присоединительные отношения между частями сложного предложения.
Член предложения
Выражение «вероятнее всего» может быть обстоятельством, сказуемым. В редких случаях оно выступает в роли предикатива. В отличие от вводного словосочетания, член предложения нельзя переставить или удалить, так как нарушится структура и смысл высказывания.
Наречие
Наречие «вероятнее всего» используется в значении «почти наверняка». Оно обозначает признак действия, связано с глаголом и отвечает на вопрос «как?».
Наречие «вероятнее всего» выполняет функцию обстоятельства образа действия. Это второстепенный член предложения, не требующий обособления запятыми.
Прилагательное
Встречается также сочетание прилагательного в форме простой сравнительной степени «вероятнее» и определительного местоимения «всего». Оно связано с существительным, выполняет функцию сказуемого и не обособляется запятыми.
Предикатив
Выражение «вероятнее всего» выступает в роли предикатива (категории состояния), если используется в значении «наиболее вероятно». Оно выполняет функцию сказуемого в безличном предложении и не требует обособления запятыми.
«Вероятно» – выделяется запятыми или нет?
Обособление вводных конструкций и действительных грамматических членов предложения — чрезвычайно трудная тема. Ученикам 8–9 классов иногда приходится заучивать каждый конкретный случай. Например, в предложениях со словом вероятно запятые ставятся или нет? Чтобы узнать это, приходится изучить контекст высказывания и проверить грамматические связи между словами.
Обособление вводного слова
В большинстве случаев «вероятно» выступает в высказывании в качестве вводного слова, которое обозначает предположение. Его используют в речи, когда говорящий не уверен, что всё именно так, как ему представляется, а только лишь предполагает это. Его синонимами могут стать «возможно», «предположительно», «я думаю, что…», «наверное» и т.д. Кроме того, «вероятно» может входить в состав обособленных оборотов — нескольких тесно связанных друг с другом слов.
Вводное «Вероятно» может выделяться знаками препинания. Есть три варианта:
его выделяют запятыми справа и слева, если оно в середине высказывания;
после этого слова, если оно расположилось в начале;
перед словом, если оно замыкает предложение.
Для проверки можно временно закрыть или выбросить вводную конструкцию из текста и посмотреть, не утратится ли смысл фразы. Если на смысле и контексте удаление никак не отразилось, значит, можно смело обособлять это слово.
Нужны ли запятые, если это член предложения?
Благодаря внимательному исследованию контекста можно узнать, «вероятно» выделяется запятыми или нет. Оно может быть наречием или краткой формой имени прилагательного и исполнять важную функцию в высказывании. Оно может выступать в качестве обстоятельства или сказуемого, тогда обосабливать его не нужно. Это слово нельзя выкинуть из текста без утраты смысла.
Например, во фразе «Завтра вероятно потепление» сказуемое не отделяют знаками препинания от других слов, которые тесно связаны с ним по смыслу и грамматически. Это главный член предложения, без которого оно будет звучать бессмысленно, поэтому его никогда не обосабливают. Если перед нами слово или их сочетание, которое играет значимую роль в высказывании, то знаки препинания не нужны. Иные варианты оказываются ошибочными.
Обособляется ли на письме частица «вероятно»?
Крайне редко это слово может играть роль частицы. В этих случаях оно либо входит в состав других членов предложения, примыкая к ним, либо вовсе к ним не относится. В обоих случаях знаки препинания рядом не требуются.
Словари
Оценочная характеристика ситуации, чьих-либо действий как возможных, допустимых.
1. Употребляется при выражении неуверенного подтверждения.
2. Употребляется как вводное слово, выражающее возможность или допустимость чего-либо и соответствующее по значению сл.: по-видимому, наверное.
1. Вы используете слово вероятно, когда хотите предположить с определённой долей уверенности, что какая-то ситуация может иметь место.
Вероятно, лифт сегодня не починят. | Этот метеорит, вероятно, упал на Землю много миллионов лет назад.
Весьма вероятно, что в новой Думе корпус депутатов обновится на две трети. | Вполне вероятно, что к концу сезона цены на этот товар резко упадут.
3. Слово вероятно можно использовать в качестве ответной реплики, когда вы не вполне уверены в том, какова ситуация на самом деле.
4. Выражение вероятнее всего используется для того, чтобы показать, что вы говорите о самом правдоподобном варианте оценки событий.
Акции этого предприятия, вероятнее всего, упадут уже к январю.
ВЕРОЯ́ТНО, вводное слово (разг.). По-видимому, надо полагать, можно думать. В шесть часов я, вероятно, буду дома.
I. нареч., в функц. сказ. Возможно, допустимо. Вполне в., что ты прав.
II. вводн. сл. По-видимому, наверно. В., сегодня задержусь. Он, в., занят.
◁ Вероя́тнее всего, в зн. вводн. словосоч. Скорее всего, почти наверняка. Вероятнее всего, дома никого нет.
Улеглись мы удобно, уютно и, вероятно, крепко бы заснули, но в самом начале сладостной дремоты нас разбудил хозяин. Гл. Успенский, Кой про что.
вводное слово, в значении сказуемого и частица
1. Вводное слово. То же, что «наверное, должно быть, по-видимому». Выделяется знаками препинания, обычно запятыми. Подробно о пунктуации при вводных словах см. в Приложении 2. (Приложение 2)
2. В значении сказуемого. Не требует постановки знаков препинания.
Очень вероятно, что рядом жертв стали неинициированные или неизвестные Темным Иные. С. Лукьяненко, Ночной дозор. Вполне вероятно, что чрезвычайные проверочные и охранные мероприятия, осуществляемые в Москве и ее окрестностях, вынудят Мищенко, Зубкова и Тулина покинуть район столицы. В. Богомолов, Момент истины. Отсутствие Федора на лекции вполне вероятно и закономерно.
3. Частица (в ответной реплике). Оформляется как отдельное предложение.
вероя́тно, вводн. сл.
нареч, кол-во синонимов: 76
возможно, видимо, по-видимому, по всей видимости (или вероятности), судя по всему, очевидно, скорее (или вернее) всего, может случиться, (очень) может быть, должно быть, верно, наверно, наверное, надо думать (или полагать), кажется, (как) видно; может, вроде (бы), пожалуй (что), как будто, думается, похоже (разг.); поди, видать, слыхать, знать, чай, считай, почитай, небось, должно, надо быть (прост.); эвентуально (книжн.); чаятельно, может статься, должно статься, должно полагать (устар.)
не исключено, что. есть шансы на что. (или что. )
/ о будущем: к тому (дело) идёт, того и гляди (разг.)
по всей вероятности
по всем видимостям
По всей вероятности, по всему вероятию, по всем вероятиям, возможно, верно, может быть, быть может, может статься, надо полагать, надо быть, должно быть, значит, знать, правдоподобно; чай, поди, небось, пожалуй; чего доброго; того и жди, едва ли не.
наверное. наверно. верно.
по всей вероятности. по всем вероятиям [вероятностям].
по-видимому. видимо. по видимости.
должно быть. надо думать [полагать]. должно (прост).
должно статься (устар).
прост: видать. знать. поди. чай. небось. надо быть.
называется биномиальным коэффициентом
(см. также НЬЮТОНА БИНОМ). Еще один полезный принцип состоит в
утверждении, что n предметов можно разложить в r коробок rn различными способами, если в любой коробке может
находиться любое число предметов. Чтобы убедиться в этом, заметим, что первый предмет можно положить в любую из r
коробок, после чего второй предмет также можно положить в любую из r коробок и т.д. Таким образом, n предметов
можно разложить 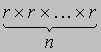
Обратимся теперь к некоторым приложениям этих принципов. 1) Какова вероятность выпадения ровно двух шестерок при пяти
бросаниях игральной кости (или, что то же, при одном бросании пяти костей)? Пять костей могут выпасть 65 способами.
Две кости, на которых выпали шестерки, можно выбрать способами (сочетания появляются потому, что порядок, в котором
выпадают шестерки, несуществен), т.е. (5*4*3*2*1)/((2*1) * (3*2*1)) = 10 способами.
Не шестерки (их 5: 1, 2, 3, 4 и 5 очков) на остальных 3 костях могут выпасть 53 способами. Следовательно, мы
получаем ровно две шестерки из пяти бросаний 10*53 способами; искомая вероятность, таким образом, равна 10*53/65
или 1250/7776, т.е. ок. 1/6. Вероятность выпадения не менее двух шестерок при пяти бросаниях кости несколько больше;
бросаниях. 2) Какова вероятность получить ровно два туза, если из колоды, состоящей из 52, извлекаются 5 карт?
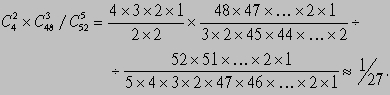
Последовательное применение такого рода рассуждений иногда приводит к удивительным заключениям.
3) Какова вероятность совпадения дней рождения по крайней мере у двух из 23 случайно выбранных людей?
Если предположить, что существует 365 равновероятных возможных дней рождения, то дни рождения 23 людей могут
распределиться (365)23 способами. Число способов, которыми можно распределить по дням года не совпадающие
на который приходится день рождения первого из них, у нас останется только 364 дня для выбора дня рождения
второго, и т.д. Вероятность несовпадения всех 23 дней рождения равна отношению второго числа к первому.
Вероятность же совпадения по крайней мере двух дней рождения равна 1 минус вероятность полного несовпадения
всех 23 дней рождения. Таким образом, ответ нашей задачи равен
При больших значениях n эта величина почти не зависит от n и равна 0,632 (с точностью до трех цифр после запятой) при n >= 6; 0,633 при n = 5; 0,625 при n = 4 и 0,667 при n = 3. Таким образом (переходя к другой, аналогичной задаче), если выкладывать по одной на стол карты из двух тщательно перетасованных колод, то выкладываемые на стол карты совпадут с вероятностью почти 2/3 по крайней мере один раз. Это утверждение верно, если в каждой колоде более двух карт.
СОВРЕМЕННАЯ ТЕОРИЯ ВЕРОЯТНОСТЕЙ
в силу чего окончательно получаем
Этот результат сводит исходную задачу к чисто комбинаторной задаче нахождения чисел m и n. Последняя легко решается с помощью теории перестановок и сочетаний, некогда бывшей существенной частью теории вероятностей, но ныне таковой не являющейся. Число n есть просто число способов, которыми можно выбрать 13 карт из 52. Используя стандартные обозначения, находим
Подобно тому, как в геометрии для строгой формулировки задачи необходимо построить пространство неопределяемых далее объектов, называемых точками, прямыми и т.д., которые удовлетворяют определенным аксиомам, формулировка вероятностной задачи требует введения пространства, называемого пространством элементарных событий, элементы которого могут быть произвольной природы и различными в разных задачах. (Хотя мы используем геометрический язык, пространство элементарных событий, как правило, не является пространством в обычном смысле;
Решение нашей задачи о вероятности того, что первый исход У наступает после k
испытаний, дается формулой
E(Z) называется «математическим ожиданием» случайной величины Z. Например, определенные выше случайные величины X и Y имеют математические ожидания
На интуитивном уровне понятие случайной величины достаточно ясно, так что оно довольно часто возникает еще до построения пространства элементарных событий. Ученый может заниматься изучением некоторой величины X, значения которой случайны либо из-за наличия экспериментальной ошибки (как в физических измерениях), либо потому, что эксперимент проводится на одном случайно выбранном элементе некоторой совокупности, состоящей из многих аналогичных элементов (например, рост какого-либо представителя расово однородной популяции взрослых или срок службы одного из изделий, выбранных из партии изделий массового производства, например плавких предохранителей, произведенных в одинаковых условиях). Возникает необходимость построить пространство элементарных событий, содержащее любое событие вида X Ј x, где x принимает действительные значения. Это можно сделать, и вероятность такого события F (x) = P
и служит удобной мерой разброса, так как равна нулю тогда и только тогда, когда случайная величина X постоянна. Две случайные величины X1 и X2, определенные на одном и том же пространстве элементарных событий, называются «независимыми», если каждое событие вида X1 Ј x не зависит от любого события вида X2 = 0
Эту теорему можно обобщить, если представить Sn как сумму независимых случайных величин
где Xk равна 1 или 0 в зависимости от того, будет ли исход k-го испытания благоприятным или неблагоприятным. Кроме того,
что позволяет записать теорему Бернулли в виде