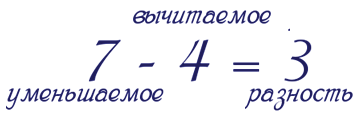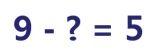Вычитание или вычетание? Как правильно и почему?
Как правильно писать: Вычитание или вычетание? Какое правило действует?
Какое проверочное слово к слову вычитание или вычетание?
Вычитание потраченных средств следует сделать сейчас.
Вычитание или вычетание?
При произношении этого слова ударным является гласный суффикса:
В написании слова «вычитание» применю орфографическое правило, согласно которому в слове пишется буква «и», если за корнем следует гласная «а», обозначающая словообразовательный суффикс.
Это условие имеется в интересующем нас слове, следовательно правильно пишется «вычитание» с буквой «и» в корне чит-.
Под данным термином подразумевают математическое действие, обратное сложению.
правописание сомнительной гласной в корне слова объясняется правилом русского языка, согласно которому в безударных корнях ЧЕТ и ЧИТ пишется буква А, если следом за корнем идёт ударный суффикс А, в противном случае пишется буква Е.
Данное правило применимо к глаголу «вычитать», а также ко всем словоформам, произошедшим от него.
По аналогии пишутся следующие слова: считать, рассчитать, высчитать, насчитать, пересчитать.
В том случае, если после корня следует суффикс «а», тогда в корне слова нужно писать гласную «и».
Правильно писать «вычитание».
Существительное пастбищего в форме родительного падежа множественного числа оканчивается на шипящий:
Правильно напишем слово «пастбищ» без мягкого знака после шипящего.
В форме родительного падежа множественного числа существительные женского рода первого склонения и существительные среднего рода второго склонения пишутся без мягкого знака, например:
В современных орфографических словарях, в частности в «Русском орфографическом словаре» РАН
под редакцией В.В. Лопатина, строго зафиксировано правописание суффикса -ОВК- после шипящих в именах существительных, образованных от других однокоренных имен существительных и прилагательных, так называемых отыменных существительных. Раньше такие слова считались исключениями и писались через гласную Ё.
Сейчас правописание таких производных слов подведено под общее правило.
Таким образом, и слово МЕЛОЧОВКА правильно писать через О, как и другие отыменные существительные, например, хрычовка, плащовка, грушовка.
Слово »добАвление» как раз относится к категории слов, проверяемых при помощи проверочного слова.
Таким проверочным словом может быть слово »добАвка», а так же глагол »добАвить».
Основное правило написания сложных слов, т.е. таких, которые образованы соединением двух основ, такое. Если новое слово образовано от равноправных слов, между которыми мы можем представить союз И, тогда пишем через дефис. Например: русско-английский словарь (в нём русские И английские слова), вогнуто-выпуклые линзы (они вогнутые И выпуклые) и т.п.
Если же новое слово образовано соединением слов из словосочетания, слов, среди которых одно главное, а второе зависимое, и мы это можем установить, задав вопрос, тогда пишем слитно. Например: многоэтажный дом (много чего? этажей), белоснежный (снег какой? белый), многовековой (веков сколько? много).
Краткие формы прилагательных пишутся с частицей «не» раздельно, если они в полной форме либо не употребляются, либо имеют другое значение.
Например, такие формы, как: не готов, не склонен, не должен пишутся только раздельно.
Пример предложения. Я не склонен менять свое мнение. Лена не склонна к полноте.
П. 7 Вычитание натуральных чисел и их свойства
Вычитание натуральных чисел
Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.

Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.
Связь вычитания и сложения
Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.
Свойства разности натуральных
чисел
Свойства разности натуральных чисел состоят из:
Рассмотрим каждый пункт подробнее.
Правила вычитания суммы из числа и числа из суммы
Как вычесть сумму из числа
Рассмотрим это на примере из урока сложение чисел.
325 +( 12 + 64 + 5 ) = 325 +81 = 406
Я запишу это в виде разности:
и покажу, что результат будет равен первому слагаемому:
Как видите, все верно.
Как вычесть число из суммы
Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.
Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:
325 +81 = ( 191 + 65 + 150 )
Превращаю выражение в разность:
( 191 + 65 + 150 )-81 = 325
и покажу, что результат также будет равен первому слагаемому:
Как меняется разность при изменении вычитаемого или уменьшаемого
Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.
Правила вычитания разности
Это свойство выводится из предыдущих, рассмотренных нами.
22 — 17 = 5
5+ 3 = 8
22 +3-( 17 +3- 3 )
25- 17 +0 = 8
Как видите, оба способа показали верный результат.
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Вычитание
Познакомимся с вычитанием.
Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
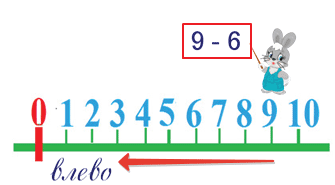
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Вычитает число 6.
Из какого числа он вычитает число 6?
Из числа 9. Мы поставили зайчика на число 9.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 6.
На каком делении он остановится? На числе 3.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
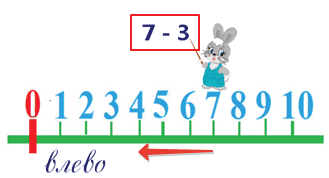
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Вычитает число 3.
Из какого числа он вычитает число 3?
Из числа 7. Мы поставили зайчика на число 7.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 3.
На каком делении он остановится? На числе 4.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
Как называются числа при вычитании?
Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют «уменьшаемое».
Число, которое вычитают, называют «вычитаемое».
Число, которое получается в результате вычитания, называют «разность».
У жонглёра было 9 шариков.
Когда несколько шариков упало, осталось ещё 5 шариков.
Сколько шариков упало?
Каким действием будем находить? Вычитанием.
Как называются числа при вычитании?
Как найти неизвестное вычитаемое
У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.
Решаем вычитанием. Что нужно найти?
Нужно найти вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Как найти неизвестное уменьшаемое
Нужно найти уменьшаемое.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
5 + 4 = 9
Проверка вычитания
Если к разности прибавить вычитаемое, получится уменьшаемое.
Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.
Правильно ли произведено вычисление? Можно проверить так:
20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.
Поделись с друзьями в социальных сетях:
Как правильно пишется слово «вычитаемое»
Источник: Орфографический академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база 2020)
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: приёмопередатчик — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «вычитаемое»
Синонимы к слову «вычитаемое»
Предложения со словом «вычитаемое»
Значение слова «вычитаемое»
Отправить комментарий
Дополнительно
Значение слова «вычитаемое»
Предложения со словом «вычитаемое»
Отложенные налоговые активы отражаются в учёте в оценке суммы, полученной как произведение вычитаемых временных разниц, возникших в отчётном периоде, на ставку налога на прибыль.
Отложенные налоговые активы принимаются к бухгалтерскому учёту в размере величины, определяемой как произведение вычитаемых разниц, возникших в отчётном периоде, на ставку налога на прибыль, действующую на отчётную дату.
Но поскольку вычитаемая величина не выражается в деньгах, проф.