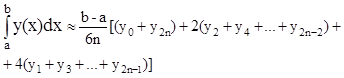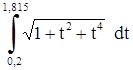Pascal: Вычисление интеграла методом Симпсона
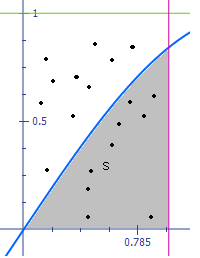
Для того, что бы понять, как это работает нужно обратиться к геометрическому смыслу интеграла. 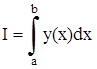
Интеграл численно равен площади криволинейной трапеции, ограниченной кривой y(x), прямыми x=a, x=b и отрезком [a; b] оси Ox.
с геометрической точки зрения означает, что график функции y(x) заменен другой кривой j(x), состоящей из дуг парабол: каждая сдвоенная дуга кривой y(x) заменяется параболой. За приближенное значение интеграла I принимается площадь криволинейной трапеции, ограниченной кривой j(x), прямыми x=x0, x=x2n и отрезком [x0, x2n]. Таким образом, решение сводится к программированию алгоритма вычисления площади криволинейной трапеции.
Программа, которая вычисляет такой интеграл:
program Simpson;
uses crt;
var
x,a,b,h,s:real;
n:integer;
8 Responses
Найдена ошибка аргумента. Исправлено.
Слишком маленькими отрезки делать тоже не стоит. Я сделал отрезкок 1/1000000, вычисления дали большую погрешность; а при отрезке 1/100000 все было приемлемо.
Может у тебя округлило?
все понял кроме этой части
begin
s:=s+4*Y(x);
x:=x+h;
s:=s+2*Y(x);
x:=x+h;
end;
s:=h/3*(s+Y(a)-Y(b));
writeln;
можешь объяснить?
С вами согласен!
C3:=h/3*(C3+y(a)+y(b));
должен быть плюс
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Вычисление определённого интеграла
Способы приближенных вычислений определенных интегралов на ЭВМ. Понятие множества в языке Паскаль, построение конкретного множественного типа. Вычисление таблицы значений функции одной переменной в среде Delphi. Особенности создания справочных систем.
| Рубрика | Программирование, компьютеры и кибернетика |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 27.07.2016 |
| Размер файла | 407,2 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru
Министерство образования Республики Беларусь
Учреждение образования «Гомельский государственный университет имени Франциска Скорины»
Кафедра вычислительной математики и программирования
ОСНОВЫ АЛГОРИТМИЗАЦИИ И ПРОГРАМММИРОВАНИЯ
студентка группы ПОСз-11
На практике часто возникает необходимость вычислить определённый интеграл. Если интеграл берётся в алгебраических функциях, то всё в порядке и взять его вручную не представляет труда. А если интеграл не берётся в алгебраических функциях или просто их очень много, то приходится прибегать к помощи компьютерной техники.
Существуют несколько способов вычисления определённых интегралов на ЭВМ, причем абсолютно все эти способы получают лишь приближённые значения:
1 формулы левых прямоугольников;
2 формулы правых прямоугольников;
3 формулы центральных прямоугольников;
4 формулы трапеций;
5 формулы Симпсона (формула парабол);
В курсовом проекте используется данные типа множества.
Понятие множества в языке Паскаль основывается на математическом представлении о конечных множествах: это ограниченная совокупность различных элементов. Для построения конкретного множественного типа используется перечисляемый или интервальный тип данных. Тип элементов, составляющих множество, называется базовым типом.
Также в курсовой работе необходимо создать файл справки. Основу справочной системы составляют темы с пояснительным текстом.
Содержание справочной системы включает список тем, доступных в системе. Каждая тема имеет заголовок и уникальный символьный идентификатор. Дополнительно каждой теме можно поставить в соответствие уникальный индекс темы, который должен быть целым числом.
Для поиска темы в справочной системе служат ключи, содержащие название темы и ссылку на нее. Каждая тема может иметь более одного ключа поиска. Кроме того, один ключ может содержать ссылку на несколько тем. интеграл множество паскаль переменная справочный
Для организации контекстного вызова темы из справочной системы вы можете использовать числовые значения индексов или значения ключа. Употребление идентификаторов тем для контекстного вывода справочной информации не допускается.
Чтобы связать между собой отдельные темы, применяются перекрестные ссылки.
При этом текст, используемый для организации перекрестной ссылки, выделяется зеленым цветом и подчеркиванием.
1. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
1.1 Основные формулы вычисления определенных интегралов
При приближённом нахождении значения определённого интеграла:
1 формула левых прямоугольников:
2 формула правых прямоугольников:
3 формула центральных прямоугольников:
4 формула трапеций:
5 формула Симпсона (формула парабол):
6 формула Ньютона (правило ):
1.2 Индивидуальное задание
Написать программу на языке Паскаль (можно и в среде Delphi), реализующую нахождение приближенного значения интеграла (согласно варианту) указанным методом.
Для проверки полученного результата необходимо найти точное значение интеграла (первообразной) и сравнить его с приближенным.
С помощью формулы центральных прямоугольников вычислить интеграл:
«Численное интегрирование в Pascal»
Государственное профессиональное образовательное учреждение
«Усинский политехнический техникум»
Научная конференция студентов
Направление: Информационные технологии
Название исследования: «Численное интегрирование в Pascal »
Хворост Мария Григорьевна
ГПОУ «УПТ», преподаватель
Появление и непрерывное совершенствование быстродействующих электронных вычислительных машин (ЭВМ) привело к подлинно революционному преобразованию науки. Изменилась технология научных исследований, колоссально увеличились возможности теоретического изучения, прогноза сложных процессов, проектирования инженерных конструкций. Решение крупных научно-технических проблем, примерами которых могут служить проблемы овладения ядерной энергией и освоения космоса, стало возможным лишь благодаря применению математического моделирования и новых численных методов, предназначенных для ЭВМ.
Многие задачи для нахождения площадей поверхностей, объемов тел и длин приводят к вычислению определенных интегралов, которые могут быть образованы очень сложной функцией или вовсе первообразная функции отсутствует. Следовательно, невозможно аналитически вычислить значение определённого интеграла по формуле Ньютона-Лейбница.
Можем ли мы найти решение данной задачи? Обратимся к численным методам.
Предмет моего исследования – решение интегралов с помощью ЭВМ.
Из цели вытекают следующие задачи:
Изучить методы численного интегрирования.
Составить алгоритм программы для вычисления поставленной задачи методом прямоугольников и трапеций.
Описание методов вычислительной математики, которые будут использованы при решении поставленной задачи.
Методы численного интегрирования, основаны на замене подынтегральной функции интерполяционным многочленом. Это позволяет приближенно заменить определенный интеграл интерполяционной суммой. В зависимости от способа ее вычисления получаются разные методы численного интегрирования:
• метод трапеций и т.д.;
На практике используют следующие методы прямоугольников:
При вычислении интеграла используют формулу трапеций
Разработка алгоритма решения задачи и написание программы
Рассмотрим задачу нахождения интеграла функции 
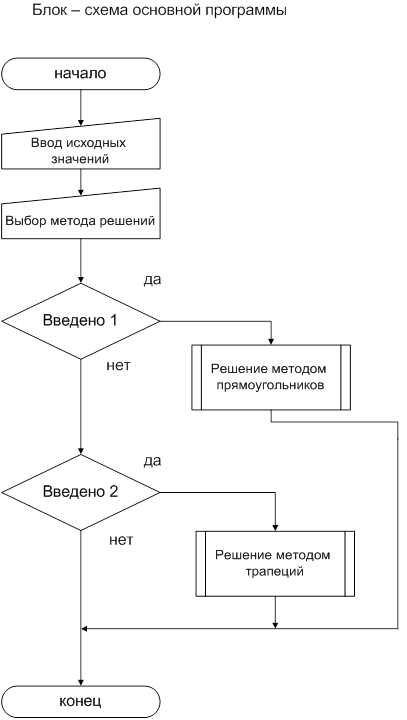
В основной программе необходимо предусмотреть ввод необходимых данных и реализацию контрольно примера, а также удобное управление элементами программы и команду выхода.
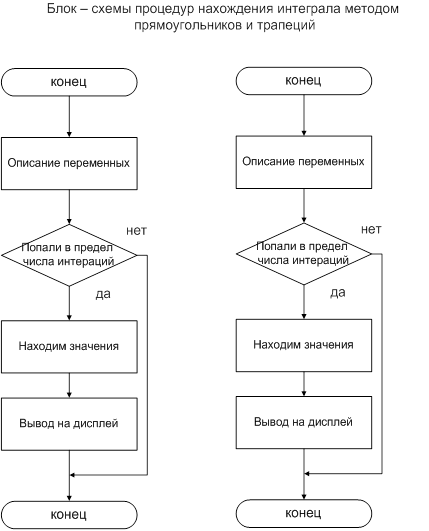
Подпрограммы реализованы в виде функций. Существует главная функция, которая вызывается из основной программы и которая выполняет основные действия (подсчет значения интеграла и вывод на экран результата, вывод графика на экран), вызывая другие подпрограммы.
Главная функция вызывает функцию подсчета интеграла с заданной точностью вычислений, которая в свою очередь на каждом шаге вызывает функцию подсчета значения функции.
Вычислите по формуле прямоугольников интеграл от функции 
Программа вычисления интеграла по методу левых прямоугольников на языке
Нахождение интегралов в среде Pascal
Нахождение интегралов в среде Pascal
Текст задания: найти интеграл функции sin (x+10)+x 4 =0 используя два метода: метод прямоугольников и метод трапеций; пользователь вводит значения и выбирает метод решения.
dx, x1, x2, e, i, c, s:real;
function Fx (x:real):real;
writeln (‘–>MEthod PRYAMOUGOL»NIKOVVVV’);
writeln (‘vsego interaciy:’, round (abs(x2-x1)/e));
for c:=1 to round (abs(x2-x1)/e) do begin
write (‘integration ‘, c, chr(13));
writeln (‘INTEGRAL=’, i);
writeln (‘–>MEthod TRAPECIY’);
writeln (‘vsego interaciy:’, round (abs(x2-x1)/e));
for c:=1 to round (abs(x2-x1)/e) do begin
write (‘Integration ‘, c, chr(13));
if xx2>xx1 then xx3:=xx1 else xx3:=xx2;
writeln (‘INTEGRAL=’, i);
writeln (‘vvedite ishodniye zna4eniya:’);
write (‘NA4AL»NOYE ZNE4ENIYE x (x1)=’); Readln(x1);
write (‘KONE4NOYE ZNA4ENIYE x (x2)=’); Readln(x2);
write (‘TO4NOST» VbI4ISLENIY (e)=’); Readln(e);
writeln (‘DLYA METODA PRYAMOUGOL»NIKOV VVEDITE 1, DLYA METODA TRAPECIY VVEDITE 2’);
//writeln (‘DLYA METODA TRAPECIY VVEDITE 2’);
Похожие работы
Вычисление интеграла, использующее начальные значения разбиений
Объясните, пожалуйста, как вычислить интеграл, используя начальные значения разбиений? В подавляющем большинстве примеров в интернете я увидел, что общее количество разбиений известно, в отличии от моего случая.
Задание: Вычислить значение определенного интеграла от выбранной подынтегральной функции и заданных с клавиатуры интервала интегрирования, точности и двух значений начальных разбиений. Например, методом левых прямоугольников.
Если более конкретно, то мне не понятно, как связать начальные значения разбиений и общее количество разбиений.

Здравствуйте! помогите пожалуйста) Вычисление значения интеграла для заданной функции на заданном.
Вычисление значения интеграла
Помогите, люди добрые. В долгу не останусь
Вычисление значения интеграла
Поомогите написать программу в C++, полную программу и если можно с объяснениями, знаю что не.

Помогите создать программу для вычисления значения интеграла от 0 до а (arctg(x)/x)dx Для.
FFPowerMan, сейчас код исправил, но все равно результата нет. Подскажите, пожалуйста, что нужно еще исправить?
Сейчас проблема в том, что если вводимые данные такие: a = 0.5, b = 5.2, e = 0.001, n1 = 2, n2 = 3, то в выводе получается: «0.58750; 20.46850; 0.39167; 7.30502; 32.12627;». То есть цикл является бесконечным, следовательно программа не заканчивается.
FFPowerMan, я написал в своей программе,
так как пользователь вводит значения начальных разбиений.
Объясните, пожалуйста, почему Вы написали так:
FFPowerMan, в последней моей версии кода, что неправильно в данном фрагменте?
Я указал на недостатки, читаем мой код и исправляем ошибки.
В Вашем коде:
не надо каждый раз умножать на h1, оно вынесено за скобки и также write не надо выводить на каждой итерации, здесь не надо, writeln потом;
по поводу 0, что это ширина поля я уже сказал;
все тоже самое для второй части.
Добавлено через 35 секунд
Не забываем про тэги кода [PASCAL][/PASCAL].
FFPowerMan, скажите, пожалуйста, что у меня неправильно в приведенном ниже коде? Я полагаю, что шаг, так как я изменяю в цикле n, от которого обратно пропорционально зависит h.
Некоторое время назад я задавал этот вопрос на этом же форуме, но собеседник не понял того, что мне не понятно, поэтому задаю вопрос второй раз.
Есть такое задание: Вычислить значение определенного интеграла от выбранной подынтегральной функции и заданных с клавиатуры интервала интегрирования, точности и значения начального разбиения методом левых прямоугольников.
Объясните, пожалуйста, чем является начальное разбиение? (например, начальным значением int или n)
В интернете я нашел много примеров, где дается значение разбиения как константа, а не значение, которое вводит пользователь и которое судя по всему может изменяться.