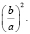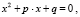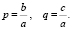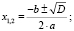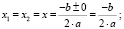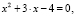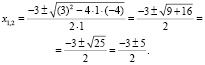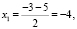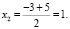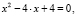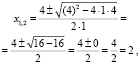Программирование на Паскале. Тема: «Решение квадратного уравнения с использованием конструкции IF–THEN–ELSE»
2. Математическое решение
Давайте вспомним, что понимают под квадратным уравнением?
Что из себя представляют числа a,b,c и как их называют?
С чего начинают решение квадратного уравнения?
Как мы решаем далее квадратное уравнение? (сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D 0, то два корня)
Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного уравнения сведу к условию D
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Сравнить его с нулём
Х1=
X2 =
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
4. Закрыть программу.
1. За простое воспроизведение (набор программы) без проверки оценка «3»
2. За проверку работы программы на примерах, представленных учителем оценка «4»
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка «5»
4. Закрыть программу.
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | 0 |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
7. Подведение итогов урока.
На сегодня наш урок закончен. До свидания.
Как написать квадратное уравнение в паскале
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений, неравенств и их систем.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Практически все, что окружает современного человека – это все так или иначе связано с математикой. Последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в дальнейшем данная тенденция сохранится. Решение многих практических задач сводится к решению различных видов уравнений. При этом актуальным является использование ЭВМ и специального ПО при решении уравнений.
Цель работы: Разработка программы нахождения корней уравнения второй степени в среде программирования Паскаль-ABC.
1) Ознакомиться с историей квадратных уравнений и методами их решения.
2) Освоить приемы программирования в интегрированной среде Паскаль-ABC.
3) Разработать алгоритм и блок-схему нахождения корней квадратных уравнений.
4) Создать программу нахождения корней и протестировать её.
Объект исследования: уравнения второй степени.
Предмет исследования: Паскаль-программа решения уравнений второй степени в среде Паскаль-ABC.
История квадратных уравнений и методы их решений
Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии, военного дела и нуждами самой математики. Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся ко второму тысячелетию до н.э. Это эпоха расцвета Вавилона и Древнего Египта.
Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и полные квадратные уравнения. Правила решения этих уравнений, изложенные в вавилонских источниках, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Герон Александрийский – греческий математик и механик. Время жизни предположительно отнесено ко второй половине I века н.э. «Метрика» Герона и извлечённые из неё «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике. Среди содержащихся в «Метрике» сведений: формулы для площадей правильных многоугольников, формула Герона для расчёта площади треугольника по длинам его сторон, правила численного решения квадратных уравнений, алгоритмы извлечения квадратных и кубических корней. В основном изложение в математических трудах Герона догматично – правила часто не выводятся, а только показываются на примерах. Герон вывел формулу для решения квадратного уравнения a•x2 + b•x = c умножением всех членов на а и прибавлением к обеим половинам уравнения выражения
Древнегреческие математики могли решать некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). В дошедших до нас шести из 13 книг «Арифметика» содержатся задачи с решениями. Способ решение полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились. Его трактат «Арифметика» содержит ряд задач, решаемых при помощи квадратных уравнений. В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.). Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: a•x 2 + b•x = c; притом предполагалось, что в нём все коэффициенты, кроме a, могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.
Абу Абдуллах (или Абу Джафар) Мухаммад ибн Муса аль-Хорезми (ок. 783-ок. 850) – один из крупнейших средневековых персидских учёных IX века, математик, астроном, географ и историк. Аль-Хорезми впервые представил алгебру как самостоятельную науку об общих методах решения линейных и квадратных уравнений, дал классификацию этих уравнений. Труды аль-Хорезми переводились с арабского на латинский язык, а затем на новые европейские языки. На их основе создавались различные учебники по математике. Аль-Хорезми известен, прежде всего, своей «Книгой о восполнении и противопоставлении» («Аль-китаб аль-мухтасар фи хисаб аль-джабр ва-ль-мукабала»), которая сыграла важнейшую роль в истории математики. От названия этой книги произошло слово «алгебра». Подлинный арабский текст утерян, однако содержание известно по латинскому переводу 1140 года английского математика Роберта Честерского. Рукопись, которую Роберт Честерский озаглавил как «Книга об алгебре и ал-мукабале» хранится в Кембридже. Другой перевод книги выполнен испанским евреем Иоанном Севильским. Задумывавшаяся как начальное руководство по практической математике «Китаб аль-джабр …» в первой (теоретической) своей части начинается с рассмотрения уравнений первой и второй степени, а в двух заключительных разделах переходит к практическому применению алгебры. Словоаль-джабр («восполнение») означало перенесение отрицательного члена из одной части уравнения в другую, а аль-мукабала («противопоставление») – сокращение равных членов в обеих частях уравнения.
Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи(он же Леонардо из Пизы или Леонардо Пизанский 1180-1240). Этот объемистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17 вв. и частично 18.
В XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет (1540-1603) впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Франсуа Виет – замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчисления. Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие математики эпохи Возрождения и подготовил почву для появления результатов Ферма, Декарта, Ньютона.
Общее правило решения квадратных уравнений, было сформулировано немецким математиком М. Штифелем (1487-1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г. Однако свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А. Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Перечислим десять способов решения квадратных уравнений:
Решение квадратных уравнений по формуле корней
Квадратное уравнение – алгебраическое уравнение общего вида
Выражение a•x2 + b•x + c называют квадратным трёхчленом.
Элементы квадратного уравнения имеют собственные названия:
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент:
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Квадратное уравнение с вещественными коэффициентами a, b cимеет ровно два комплексных корня, о чём гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта 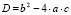
4. Если D = 0, то вычислить и напечатать значение x1 = x2 = x и перейти к п. 6. Иначе перейти к п. 5.
5. Вычислить действительную и мнимую части комплексных корней и напечатать значения пары комплексно сопряженных корней.
6. Прекратить вычисления.
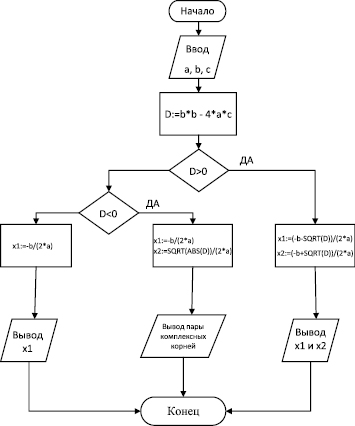
Представим разработанный выше алгоритм в виде блок-схемы.
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур – блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19.701-90.
Интегрированная среда программирования Паскаль-ABC. Разработка и тестирование программы
Наиболее распространенным в настоящее время языком программирования для компьютеров серии IBM PC является Паскаль. Это язык высокого уровня, отличающийся простотой синтаксиса, структурированный и удобный для начального обучения программированию.
Система Паскаль-ABC предназначена для обучения программированию на языке Паскаль и ориентирована на школьников и студентов младших курсов. По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близки к стандартным и иметь богатые и современные библиотеки подпрограмм.
Система программирования Паскаль-ABC представляет собой единство компилятора языка программирования Паскаль и инструментальной программной оболочки, называемой средой. Среда предоставляет необходимые сервисные услуги и способствует повышению эффективности процессов разработки, отладки и испытаний программ, что облегчает труд программиста.
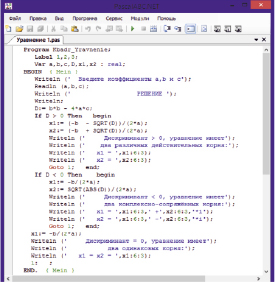
Рис. 2. Скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC
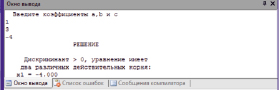
Рис. 3. Скриншот результата вычислений действительных различных корней
На рис. 2 представлен скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC. Т.к. программа имеет три разветвления, то протестируем каждую из ветвей.
Решим квадратное уравнение, имеющее два действительных корня (D > 0):
Здесь 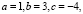
Тогда, вычисленные корни имеют вид:
Скриншот полученного результата представлен на рис. 3.
Решим квадратное уравнение, имеющее один действительный корень (D = 0):
Здесь 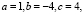
Скриншот полученного результата представлен на рис. 4.
Решим квадратное уравнение, имеющее пару комплексно сопряженных корней (D
Как написать квадратное уравнение в паскале
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений, неравенств и их систем.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Практически все, что окружает современного человека – это все так или иначе связано с математикой. Последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в дальнейшем данная тенденция сохранится. Решение многих практических задач сводится к решению различных видов уравнений. При этом актуальным является использование ЭВМ и специального ПО при решении уравнений.
Цель работы: Разработка программы нахождения корней уравнения второй степени в среде программирования Паскаль-ABC.
1) Ознакомиться с историей квадратных уравнений и методами их решения.
2) Освоить приемы программирования в интегрированной среде Паскаль-ABC.
3) Разработать алгоритм и блок-схему нахождения корней квадратных уравнений.
4) Создать программу нахождения корней и протестировать её.
Объект исследования: уравнения второй степени.
Предмет исследования: Паскаль-программа решения уравнений второй степени в среде Паскаль-ABC.
История квадратных уравнений и методы их решений
Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии, военного дела и нуждами самой математики. Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся ко второму тысячелетию до н.э. Это эпоха расцвета Вавилона и Древнего Египта.
Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и полные квадратные уравнения. Правила решения этих уравнений, изложенные в вавилонских источниках, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Герон Александрийский – греческий математик и механик. Время жизни предположительно отнесено ко второй половине I века н.э. «Метрика» Герона и извлечённые из неё «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике. Среди содержащихся в «Метрике» сведений: формулы для площадей правильных многоугольников, формула Герона для расчёта площади треугольника по длинам его сторон, правила численного решения квадратных уравнений, алгоритмы извлечения квадратных и кубических корней. В основном изложение в математических трудах Герона догматично – правила часто не выводятся, а только показываются на примерах. Герон вывел формулу для решения квадратного уравнения a•x2 + b•x = c умножением всех членов на а и прибавлением к обеим половинам уравнения выражения
Древнегреческие математики могли решать некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). В дошедших до нас шести из 13 книг «Арифметика» содержатся задачи с решениями. Способ решение полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились. Его трактат «Арифметика» содержит ряд задач, решаемых при помощи квадратных уравнений. В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.). Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: a•x 2 + b•x = c; притом предполагалось, что в нём все коэффициенты, кроме a, могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.
Абу Абдуллах (или Абу Джафар) Мухаммад ибн Муса аль-Хорезми (ок. 783-ок. 850) – один из крупнейших средневековых персидских учёных IX века, математик, астроном, географ и историк. Аль-Хорезми впервые представил алгебру как самостоятельную науку об общих методах решения линейных и квадратных уравнений, дал классификацию этих уравнений. Труды аль-Хорезми переводились с арабского на латинский язык, а затем на новые европейские языки. На их основе создавались различные учебники по математике. Аль-Хорезми известен, прежде всего, своей «Книгой о восполнении и противопоставлении» («Аль-китаб аль-мухтасар фи хисаб аль-джабр ва-ль-мукабала»), которая сыграла важнейшую роль в истории математики. От названия этой книги произошло слово «алгебра». Подлинный арабский текст утерян, однако содержание известно по латинскому переводу 1140 года английского математика Роберта Честерского. Рукопись, которую Роберт Честерский озаглавил как «Книга об алгебре и ал-мукабале» хранится в Кембридже. Другой перевод книги выполнен испанским евреем Иоанном Севильским. Задумывавшаяся как начальное руководство по практической математике «Китаб аль-джабр …» в первой (теоретической) своей части начинается с рассмотрения уравнений первой и второй степени, а в двух заключительных разделах переходит к практическому применению алгебры. Словоаль-джабр («восполнение») означало перенесение отрицательного члена из одной части уравнения в другую, а аль-мукабала («противопоставление») – сокращение равных членов в обеих частях уравнения.
Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи(он же Леонардо из Пизы или Леонардо Пизанский 1180-1240). Этот объемистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17 вв. и частично 18.
В XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет (1540-1603) впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Франсуа Виет – замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчисления. Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие математики эпохи Возрождения и подготовил почву для появления результатов Ферма, Декарта, Ньютона.
Общее правило решения квадратных уравнений, было сформулировано немецким математиком М. Штифелем (1487-1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г. Однако свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А. Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Перечислим десять способов решения квадратных уравнений:
Решение квадратных уравнений по формуле корней
Квадратное уравнение – алгебраическое уравнение общего вида
Выражение a•x2 + b•x + c называют квадратным трёхчленом.
Элементы квадратного уравнения имеют собственные названия:
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент:
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Квадратное уравнение с вещественными коэффициентами a, b cимеет ровно два комплексных корня, о чём гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта 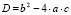
4. Если D = 0, то вычислить и напечатать значение x1 = x2 = x и перейти к п. 6. Иначе перейти к п. 5.
5. Вычислить действительную и мнимую части комплексных корней и напечатать значения пары комплексно сопряженных корней.
6. Прекратить вычисления.
Представим разработанный выше алгоритм в виде блок-схемы.
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур – блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19.701-90.
Интегрированная среда программирования Паскаль-ABC. Разработка и тестирование программы
Наиболее распространенным в настоящее время языком программирования для компьютеров серии IBM PC является Паскаль. Это язык высокого уровня, отличающийся простотой синтаксиса, структурированный и удобный для начального обучения программированию.
Система Паскаль-ABC предназначена для обучения программированию на языке Паскаль и ориентирована на школьников и студентов младших курсов. По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близки к стандартным и иметь богатые и современные библиотеки подпрограмм.
Система программирования Паскаль-ABC представляет собой единство компилятора языка программирования Паскаль и инструментальной программной оболочки, называемой средой. Среда предоставляет необходимые сервисные услуги и способствует повышению эффективности процессов разработки, отладки и испытаний программ, что облегчает труд программиста.
Рис. 2. Скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC
Рис. 3. Скриншот результата вычислений действительных различных корней
На рис. 2 представлен скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC. Т.к. программа имеет три разветвления, то протестируем каждую из ветвей.
Решим квадратное уравнение, имеющее два действительных корня (D > 0):
Здесь 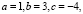
Тогда, вычисленные корни имеют вид:
Скриншот полученного результата представлен на рис. 3.
Решим квадратное уравнение, имеющее один действительный корень (D = 0):
Здесь 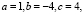
Скриншот полученного результата представлен на рис. 4.
Решим квадратное уравнение, имеющее пару комплексно сопряженных корней (D