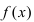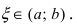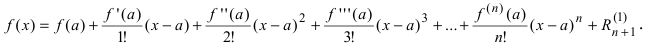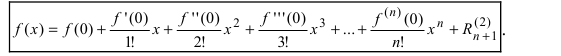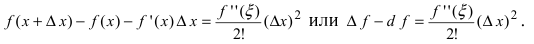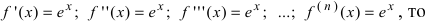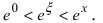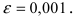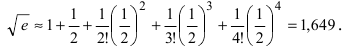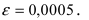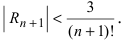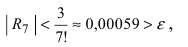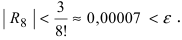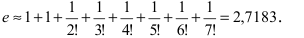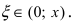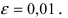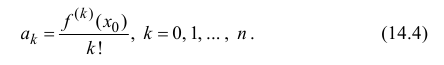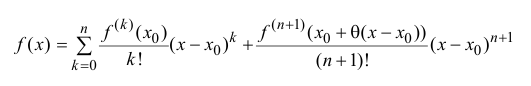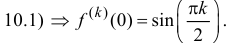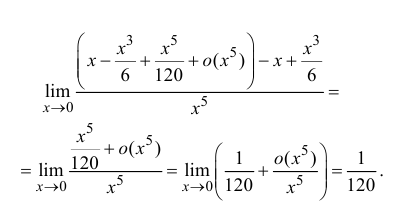Слово Как написать многочлен тейлора - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Формула Тейлора и ее применение с примерами решения

Содержание:

Формула Тейлора и ее применение

Формула Тейлора

Теорема: Если функция

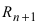
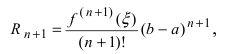
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора называется остаточным членом, вид которого установил Лагранж: величина

В этой формуле неизвестной является только величина 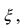причем в указанном интервале согласно теореме Лагранжа такая точка всегда присутствует, хотя бы в единственном числе. Если зафиксировать начало интервала, а его конец считать переменной величиной, то формула Тейлора принимает вид:

При a = 0 формула Тейлора переходит в формулу Маклoрена:

Пример:

Представить по формуле Маклорена функцию 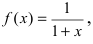ограничившись n=2.

Решение:

Вычислим три первых производных заданной функции:

При х = 0 получим Остаточный член имеет вид Следовательно, при n = 2 заданная функция по формуле Маклорена имеет вид: Отметим, что полученное выражение справедливо при Решим найденное равенство относительно величины Отсюда получаем Следовательно, Так как выражение под радикалом 4-ой степени должно быть неотрицательным и Таким образом, из двух корней теореме Тейлора удовлетворяет только корень который действительно лежит между нулем и х.

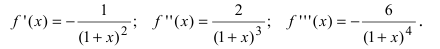
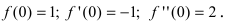
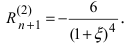
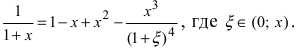
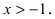
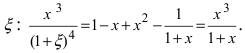
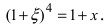
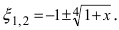
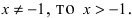
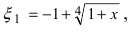
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:

(см. теорему Лагранжа ТЗ Лекции №18). При n = 1 получаем Если положить то получим формулу

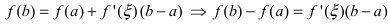
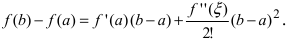
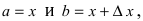
Применение формулы Тейлора

Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 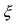в остаточном члене в форме Лагранжа лежит в пределах от а до х.

Пример:

Представить функцию 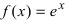по формуле Маклорена.

Решение:

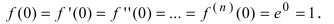
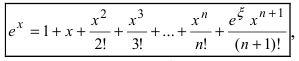
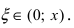
Так как Следовательно, где Отсюда следует,

Пример:

Вычислить 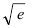с точностью

Решение:

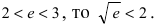
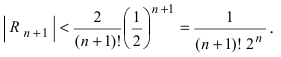
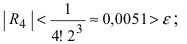
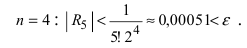
Так как основание Следовательно, при х = 1/2 остаточный член равен При n = 3: остаточный член Следовательно, удерживая пять первых слагаемых в формуле Маклорена, получим с требуемой точностью, что

Пример:

Вычислить число е с точностью

Решение:

Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа

При n = 6 имеем

при n = 7 получаем

Итак,

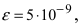
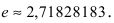
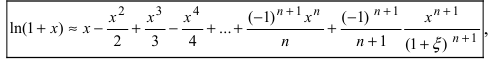
Если вычислять значение числа е с точностью то потребуется взять 13 первых слагаемых, при этом Аналогично формула Маклорена-Тейлора применяется для вычисления и других функций. Например, для вычисления натуральных логарифмов используется формула:причем

Пример:

Вычислить 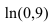с точностью

Решение:

Формула тейлора

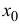
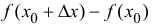
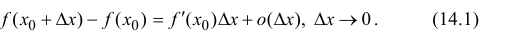
Пусть функция y=f(x) дифференцируема в точке . Тогда (см. формулу (9.5)) ее приращение

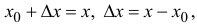
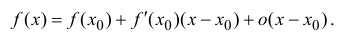
Пусть тогда (14.1) перепишется в виде
Рассмотрим многочлен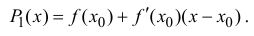
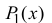
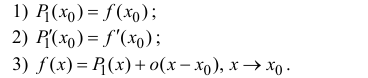
Многочлен обладает следующими свойствами:

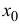
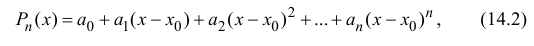
Пусть функция y=f(x) n раз дифференцируема в точке . Найдем многочлен

обладающий аналогичными свойствами: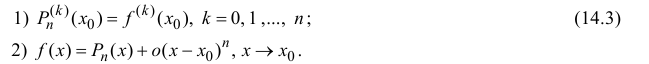

Из (14.2), (14.3) следует, что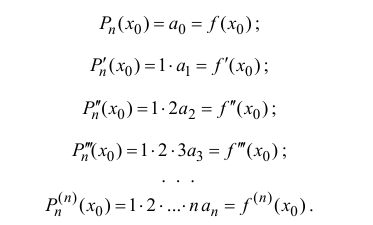

Поэтому коэффициенты 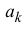многочлена (14.2) задаются формулой

Далее

Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 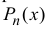задаются формулами (14.4)). Тем самым теорема доказана.
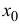
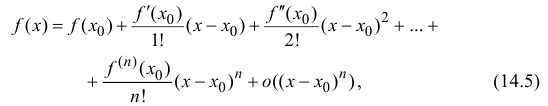
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке , тогда

где 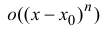– бесконечно малая функция более высокого порядка
малости, чем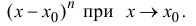
Формула (14.5) называется формулой Тейлора, многочлен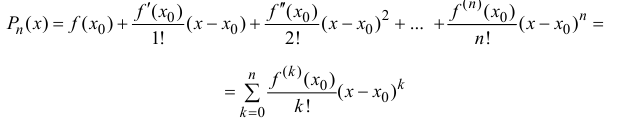

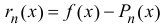
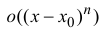
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности в виде – остаточным членом в форме Пеано.
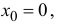
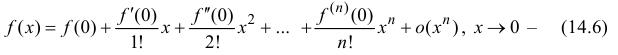
Если функция то (14.5) перепишется в виде

формула Маклорена.
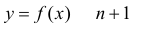
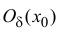
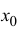
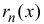
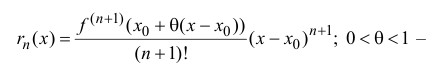
Если функция раз дифференцируема в некоторой окрестности
точки , то остаточный член можно представить в виде
остаточный член в форме Лагранжа и формула

называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.

Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений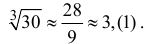
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа: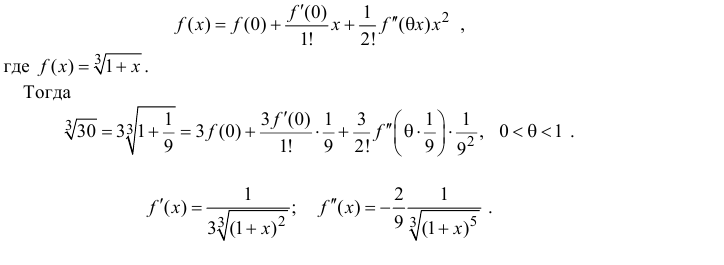

Поэтому

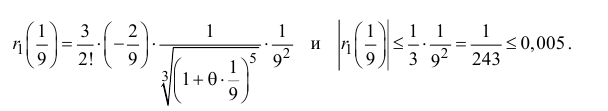
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.

Пример 14.2
Запишем формулу Маклорена n-го порядка для функции y=sin x: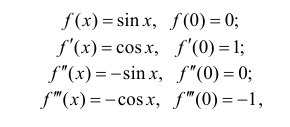

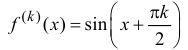
(см. упражнение 10.1)

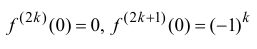
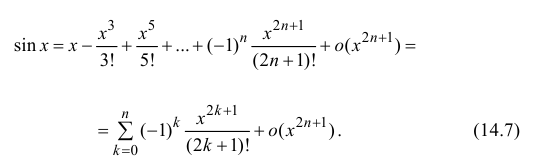
Таким образом, и по формуле (14.6)

Аналогично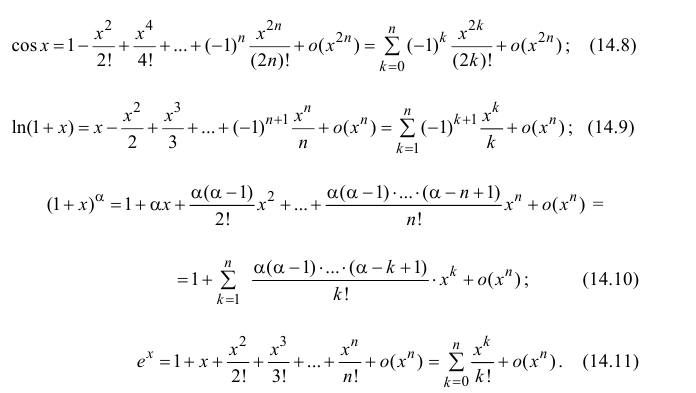

Формулы (14.7)–(14.11) называются основными разложениями.

Пример 14.3
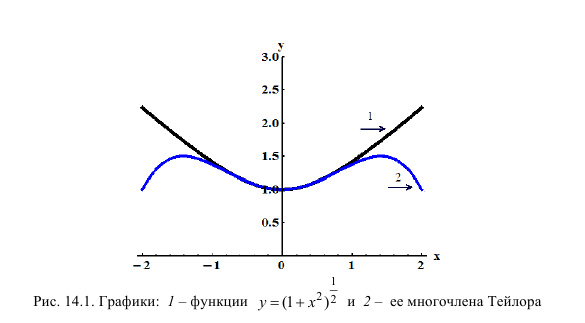
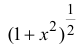
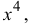
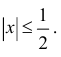
Разложить по формуле Маклорена до члена используя основные разложения. Оценить погрешность при
Решение
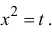
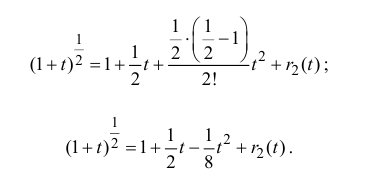
Пусть Тогда (см. формулу (14.10))

Остаточный член запишем в форме Лагранжа: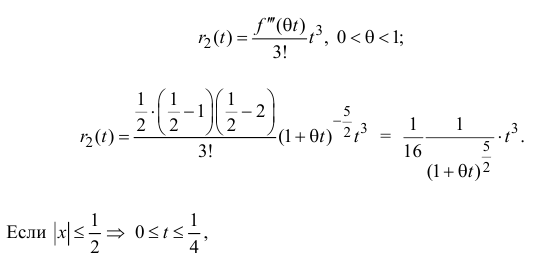

поэтому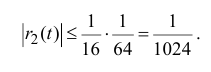
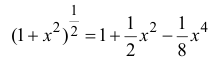
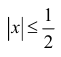
Таким образом, и погрешность при меньше чем

Пример 14.4
Найти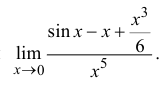
Решение
Воспользуемся разложением (14.7):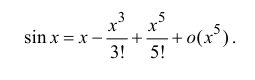

Тогда

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Формула Тейлора

Формула Тейлора с остаточным членом в форме Лагранжа.

Если функция \(f(x)\) имеет в точке \(x_<0>\) производную n-го порядка, то существует многочлен \(P_(x)\) степени не выше n такой, что
$$
P_n(x_0)=f(x_<0>),\ P_^<(k)>(x_<0>)=f^<(k)>(x_<0>),\ k=\overline<1,n>.\label
$$
Этот многочлен представляется в виде
$$
P_n(x)=f(x_<0>)+\frac)><1!>(x-x_0)+\frac<2!>(x-x_0)^2+\ldots+\frac(x_0)>(x-x_0)^n.\label
$$

\(\circ\) Пусть \(\varphi(x)=(x-x_0)^m\), где \(m\in\mathbb\). Тогда \(\varphi(x_0)=0\),
$$
\varphi^<(k)>(x_<0>)=\left\<\begin
0, & если \ k\neq m,\\
k!, & если \ k=m.
\end\right.\label
$$
Из \eqref следует, что многочлен \(P_n(x)\), заданный формулой \eqref, удовлетворяет условиям \eqref. Этот многочлен называют многочленом Тейлора n-го порядка для функции \(f(x)\) в точке \(x_<0>\). \(\bullet\)

Пусть функции \(f(x)\) и \(\psi(x)\) определены в \(\delta\)-окрестности точки \(x_0\) и удовлетворяют следующим условиям:

Тогда для каждого \(x\in\dot_<\delta>(x_<0>)\) существует точка \(\xi\), принадлежащая интервалу с концами \(x_0\) и \(x\) такая, что
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi^<(n+1)>(\xi)><\psi^<(n+1)>(\xi)>.\label
$$

\(\circ\) Пусть, например, \(x\in(x_0,x_0+\delta)\). Тогда, применяя к функциям \(\varphi\) и \(\psi\) на отрезке \([x_0,x]\) теорему Коши и учитывая, что \(\varphi(x_0)=\psi(x_0)=0\) в силу условий \eqref, получаем
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi(x)-\varphi(x_0)><\psi(x)-\psi(x_0)>=\frac<\varphi'(\xi_1)><\psi'(\xi_1)>\quad x_0 Теорема 1.

Пусть существует \(\delta >0\) такое, что функция \(f(x)\) имеет в \(\delta\)-окрестности точки \(x_0\) производные до \((n+1)\)-го порядка включительно.

Тогда для любого \(x\in\dot_\delta(x_0)\) найдется точка \(\xi\), принадлежащая интервалу \(\Delta\) с концами \(x_<0>\) и \(x\), такая, что
$$
f(x)=f(x_0)+\frac)><1!>(x-x_0)+\ldots+\frac(x_<0>)>(x-x_0)^n+\frac(\xi)><(n+1)!>(x-x_<0>)^.\label
$$

\(\circ\) Пусть \(x\in\dot_\delta(x_0)\), \(P_n(x)=\displaystyle \sum_^\frac(x_<0>)>(x-x_0)^k\) — многочлен Тейлора для функции \(f(x)\). Обозначим
$$
r_(x)=f(x)-P_n(x).\label
$$
Так как многочлен \(P_(x)\) удовлетворяет в силу леммы 1 условиям \eqref, то из равенства \eqref следует, что
$$
r_n(x_0)=r_n'(x_0)=\ldots=r_^<(n)>(x_<0>)=0.\label
$$
Рассмотрим функции \(\varphi(x)=r_n(x)\), \(\psi(x)=(x-x_0)^\). Эти функции удовлетворяют условиям леммы 2, и поэтому для них выполняется равенство \eqref, то есть
$$
\frac<\varphi(x)><\psi(x)>=\frac<(x-x_0)^>=\frac(\xi)><(n+1)!>=\frac(\xi)><(n+1)!>,\quad\xi\in\Delta,\label
$$
так как \(P_n^<(n+1)>(x)\equiv 0,\ \psi^<(n+1)>(x)=(n+1)!\) Из равенств \eqref и \eqref следует формула \eqref. \(\bullet\)

Функцию \(r_n(x)=\displaystyle \frac(\xi)><(n+1)!>(x-x_0)^\) называют остаточным членом формулы Тейлора в форме Лагранжа. Формула \eqref справедлива и при \(x=x_<0>\).

Если функции \(\varphi\) и \(\psi\) дифференцируемы \(n\) раз при \(x\geq x_<0>\) и удовлетворяют условиям \(\varphi^<(k)>(x_<0>)=\psi^<(k)>(x_<0>)\), \(k=\overline<0,n-1>\), \(\varphi^<(n)>(x)>\psi^<(n)>(x)\) при \(x > x_0\), то \(\varphi(x) > \psi(x)\) при \(x > x_<0>\).

\(\circ\) Для \(n=1\) утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим \(f(x)=\varphi(x)-\psi(x)\). Тогда \(f^<(k)>(x_<0>)=0\) при \(k=\overline<0,n-1>0\), и по формуле \eqref получаем
$$
f(x)=\frac<1>(x-x_<0>)^f^<(n)>(\xi).\nonumber
$$
Если \( x> x_<0>\), то \(\xi > x_0\), \(f^<(n)>(\xi)=\varphi^<(n)>(\xi)-\psi^<(n)>(\xi) > 0\), и поэтому \(f(x) > 0\), то есть \(\varphi(x) > \psi(x)\) при \(x > x_<0>\). \(\bullet\)

Формула Тейлора с остаточным членом в форме Пеано.

Из существования \(f^<(n)>(x_0)\) следует, что функция \(f(x)\) определена и имеет производные до \((n-1)\)-го порядка включительно в \(\delta\)-окрестности точки \(x_0\). Обозначим \(\varphi(x)=r_n(x)\), \(\psi(x)=(x-x_0)^n\), где функция \(r_n(x)\) определяется формулой \eqref. Функции \(\varphi(x)\) и \(\psi(x)\) удовлетворяют условиям леммы 2, если заменить номер \(n+1\) на номер \(n-1\) (см. равенства \eqref). Используя лемму 2 и учитывая, что \(r_n^<(n-1)>(x_0)=0\), получаем
$$
\frac<(x-x_0)^n>=\frac(\xi)-r_n^(x_0)>)>,\label
$$
где \(\xi=\xi(x)\) и
$$
x_0 Замечание 2.

Формулу \eqref часто называют формулой Тейлора с остаточным членом в форме Пеано или локальной формулой Тейлора.

Разложить функцию \(f(x)\) по формуле Тейлора в окрестности точки \(x_0\) до \(o((x-x_0)^n)\) — значит представить ее в виде \eqref.

\(\circ\) По теореме 2 справедлива формула \eqref, и так как по условию выполняется равенство \eqref, то
$$
a_0+a_1(x-x_0)+\ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\\=f(x_<0>)+f'(x_<0>)(x-x_0)+\ldots+f^<(n)>(x_<0>)\frac<(x-x_<0>)^>+o((x-x_0)^n).\label
$$
Переходя к пределу при \(x\rightarrow x_<0>\) в равенстве \eqref, получаем \(a_<0>=f(x_<0>)\). Отбросив в левой и правой частях этого равенства одинаковые слагаемые \(a_<0>\) и \(f(x_<0>)\) и разделив обе части полученного равенства на \(x-x_0\), имеем
$$
a_1+a_2(x-x_0)+\ldots+a_n(x-x_0)^+o((x-x_0)^)=\\=f'(x_0)+\frac)><2!>(x-x_0)+\ldots+\frac(x_<0>)>(x-x_0)^+o((x-x_0)^).
$$
Переходя в этом равенстве к пределу при \(x\rightarrow x_0\), находим \(f'(x_<0>)=a_<1>\). Продолжая эти рассуждения, получаем равенства \eqref. \(\bullet\)

Теорема 3 означает, что представление в виде \eqref функции, имеющей в точке \(x_<0>\) производную \(n\)-го порядка, единственно: коэффициенты разложения \eqref выражаются по формулам \eqref.

Разложить функцию \(\displaystyle \frac<1><1-x>\) по формуле Тейлора в окрестности точки \(x_<0>=0\) до \(o(x^)\).

\(\triangle\) Воспользуемся равенством \((1+x+\ldots+x^)(1-x)=1-x^\), откуда \(\displaystyle \frac<1><1-x>=1+x+\ldots+x^n+r_n(x)\), где \(r_n(x)=\displaystyle \frac><1-x>=o(x^)\) при \(x\rightarrow 0\). Таким образом,
$$
\frac<1><1-x>=1+x+\ldots+x^n+o(x^n).\label
$$
Так как функция \(\displaystyle \frac<1><1-x>\) бесконечно дифференцируема при \(x\neq 1\) (имеет производные любого порядка), то по теореме 3 формула \eqref дает искомое разложение. \(\blacktriangle\)

Разложение основных элементарных функций по формуле Тейлора.

Если \(x_<0>=0\) и существует \(f^<(n)>(0)\), то равенство \eqref принимает вид
$$
f(x)=\sum_^\frac>x^k+o(x^n),\ x\rightarrow 0.\label
$$
Формулу \eqref называют формулой Маклорена.

Пусть, функция \(f(x)\) бесконечно дифференцируема на интервале \((-l,l)\). Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции \(f\) выполняются условия \(f^<(2k)>(0)=0\), \(k\in\mathbb\), а для четной функции \(f\) — условия \(f^<(2k-1)>(0)=0\), \(k\in\mathbb\), так как любая непрерывная нечетная функция принимает при \(x=0\) значение нуль.

Поэтому формулу \eqref для бесконечно дифференцируемой четной функции можно записать в виде
$$
f(x)=\sum_^\frac(0)><(2k)!>x^<2k>+o(x^<2n+2>),\quad x\rightarrow 0,\label
$$
а для нечетной функции — в виде
$$
f(x)=\sum_^\frac(0)><(2k+1)!>x^<2k+1>+o(x^<2n+2>),\quad x\rightarrow 0,\label
$$
В формуле \eqref остаточный член записан в виде \(o(x^<(2n+1)>)\), а не в виде \(о(x^<2n>)\), так как для четной функции \(f\) выполняется условие \(f^<(2n+1)>(0)=0\), и поэтому член многочлена Тейлора, который следует за слагаемым \(\displaystyle\frac(0)><(2n)!>x^<2n>\) равен нулю. Аналогично рассматривается вопрос о записи остаточного члена формулы \eqref.

Показательная функция.

Гиперболические функции.

Так как \(\operatornamex=\displaystyle \frac-e^<-x>><2>\), \(\operatornamex=\displaystyle \frac+e^<-x>><2>\), то формулы \eqref и \eqref можно получить, используя равенство \eqref и равенство \(e^<-x>=\displaystyle \sum_^\frac<(-1)^x^>+о(x^),\ x\rightarrow 0\).

Источник