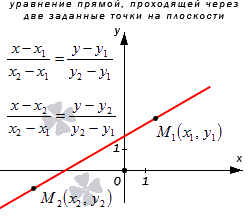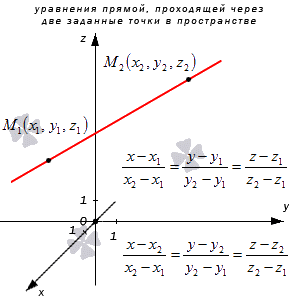Слово Как написать общее уравнение прямой по двум точкам в пространстве - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Уравнение прямой, проходящей через две точки онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Уравнение прямой, проходящей через две точки − примеры и решения

Подставив координаты точек A и B в уравнение (1), получим:

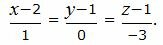(Здесь 0 в знаменателе не означает деление на 0).

Составим параметрическое уравнение прямой:

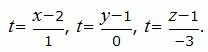Выразим переменные x, y, z через параметр t :

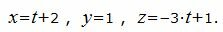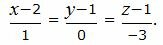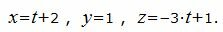Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).

Подставив координаты точек A и B в уравнение (2), получим:

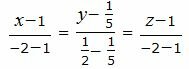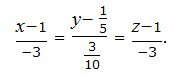Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :

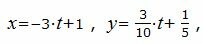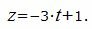Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

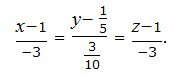Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

Источник

Уравнение прямой, которая проходит через две заданные точки: примеры, решения

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим рисунок, приведенный ниже.

Рассмотрим подробней на решении нескольких примеров.

При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Приведем каноническое уравнение к искомому виду, тогда получим:

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

При подстановке получаем, что

Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

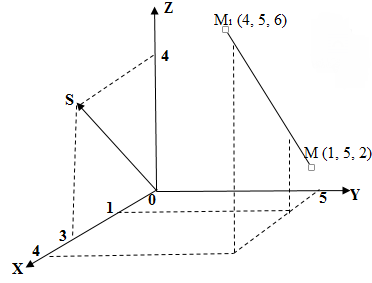
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.

Источник

Уравнение прямой

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

Уравнение прямой в отрезках на осях

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки M( x ₁, y ₁) и N( x ₂, y ₂), такие что x ₁ ≠ x ₂ и y ₁ ≠ y ₂, то уравнение прямой можно найти, используя следующую формулу

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x ₀ y = m t + y ₀

Каноническое уравнение прямой на плоскости

Если известны координаты точки N( x ₀, y ₀) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки

Упростив это уравнение получим каноническое уравнение прямой

Выразим y через x и получим уравнение прямой с угловым коэффициентом

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Если прямая проходит через две точки M( x ₁, y ₁, z ₁) и N( x ₂, y ₂, z ₂), такие что x ₁ ≠ x ₂, y ₁ ≠ y ₂ и z ₁ ≠ z ₂, то уравнение прямой можно найти используя следующую формулу

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x 0
	y = m t + y 0
	z = n t + z 0

Каноническое уравнение прямой в пространстве

Если известны координаты точки M( x ₀, y ₀, z ₀) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу

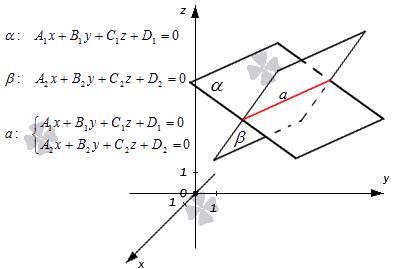
Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

	A1 x + B1 y + C1 z + D1 = 0
	A2 x + B2 y + C2 z + D2 = 0

при условии, что не имеет место равенство

A1	=	B1	=	C1	.
A2		B2		C2

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Уравнения прямой, виды уравнений прямой в пространстве

Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.

Уравнение прямой в пространстве: общие сведения

Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей

Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.

Рассмотрим это утверждение в алгебраическом толковании.

Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Резюмируем: прямая в пространстве в прямоугольной системе координат O x y z может быть задана системой уравнений двух плоскостей, которые пересекаются:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Приведем пример описания прямой линии в пространстве при помощи системы уравнений:

Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.

Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.

Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.

Параметрические уравнения прямой в пространстве

x = x 1 + a x · 0 y = y 1 + a y · 0 z = z 1 + a z · 0 ⇔ x = x 1 y = y 1 z = z 1

Рассмотрим конкретный пример:

Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.

Канонические уравнения прямой в пространстве

Если разрешить каждое из параметрических уравнений прямой

Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.

Источник

Прямая в пространстве – виды уравнения прямой в пространстве

Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.

Параметрическое и каноническое уравнение прямой в пространстве

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку параллельно направляющему вектору .

Пусть, – произвольная точка прямой, тогда векторы и коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

это и есть канонические уравнения прямой.

Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки и можно не только геометрично провести линию, но и сложить её уравнения.

За направляющий вектор возьмём , тогда по формуле (1) у нас получается:

уравнение прямой в пространстве, которые проходят через две заданные точки.

Нужна помощь в написании работы?

Общее уравнение прямой – переход к каноническому уравнению

Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

Пусть известны их уравнения:

Тогда система (4) называется общим уравнением прямой.

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку этой прямой.

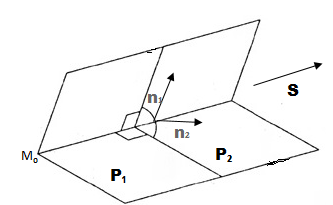
Точку находим, как один из решений системы (4). Например, положив в (4) находим , тогда и точку . Направляющий вектор , который параллелен к каждой из плоскостей и и перпендикулярен к их нормальным векторам и , то есть , . (см. рис. 1). Поэтому вектор можно найти при помощи векторного произведения и

= x =

Найдены координаты и подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём . Нормальные векторы и . Тогда направляющий вектор

x = ,

и канонические уравнения станут:

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми :

и

равен углу между их направляющими векторами и , поэтому

=

Условия параллельности и перпендикулярности прямых соответственно запишутся:

и .

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

Задача

При точке и направляющем векторе необходимо:

Решение

1) По формуле (1) запишем каноническое уравнение прямой :

= .

2) Рассмотрим два способа построения прямой .

Первый способ

В системе координат строим вектор и точку и проводим через точку прямую параллельную вектору .

Второй способ

По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:

На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой . Так при находим координаты . Через две точки и проводим прямую .

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

Задача

Найти острый угол между прямыми:

,

Решение

По формуле (7) получаем:

= = =

Так как , тогда угол тупой, , а острый угол .

Ответ

.

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

Задача

Составить уравнение прямой , которая проходит через точку и параллельна прямой .

Решение

От параметрического уравнения переходим к каноническому При условии параллельности прямых то есть направляющим вектором новой прямой может служить известный вектор и по формуле (1) у нас получается:

.

Ответ

.

Источник