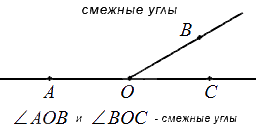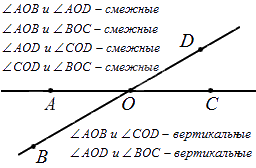Слово Как написать острый угол - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Острый угол

Острый угол — это угол, меньший прямого.

Градусная мера острого угла больше нуля, но меньше 90 градусов.

∠ABC, ∠MNK, ∠DEF — острые углы.

Чтобы построить острый угол заданной градусной меры, пользуются транспортиром.

Построить с помощью транспортира угол 72º.

1) Отмечаем точку — вершину угла.

2) От точки проводим луч — сторону угла.

3) Совмещаем вершину угла с отметкой в центре транспортира (у разных моделей транспортира положение этой отметки может быть разным) так, чтобы отметка 0º была расположена на стороне угла.

4) Находим 72º на той шкале, где находится 0º, и ставим точку.

5) От вершины угла через отмеченную точку проводим луч — вторую сторону угла.

На рисунках изображено построение угла 72º с началом отсчёта по нижней шкале и с началом отсчёта по верхней шкале.

∠ABC=72º

∠CDE=72º

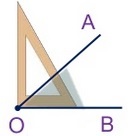
Чтобы определить по рисунку, является ли угол острым, можно воспользоваться угольником. Если приложить вершину угольника к вершине угла так, чтобы сторона угольника прошла через одну сторону угла, то другая сторона угольника закроет вторую сторону угла:

Источник

Как написать острый угол

Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.

Лучи называются сторонами угла, а их общее начало − вершиной угла.

Обозначение угла

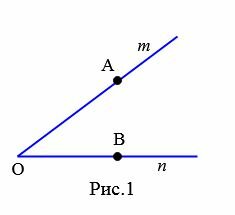
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)

Развернутый угол. Внутренняя и внешняя область угла

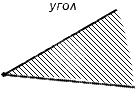
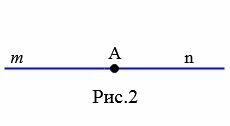
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.

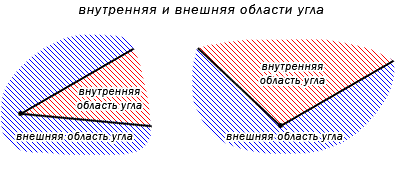
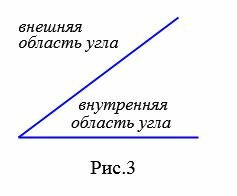
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).

Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.

Фигуру, состоящую из угла и его внутренней области также называют углом.

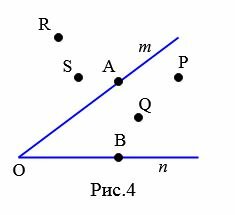
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.

Типы углов

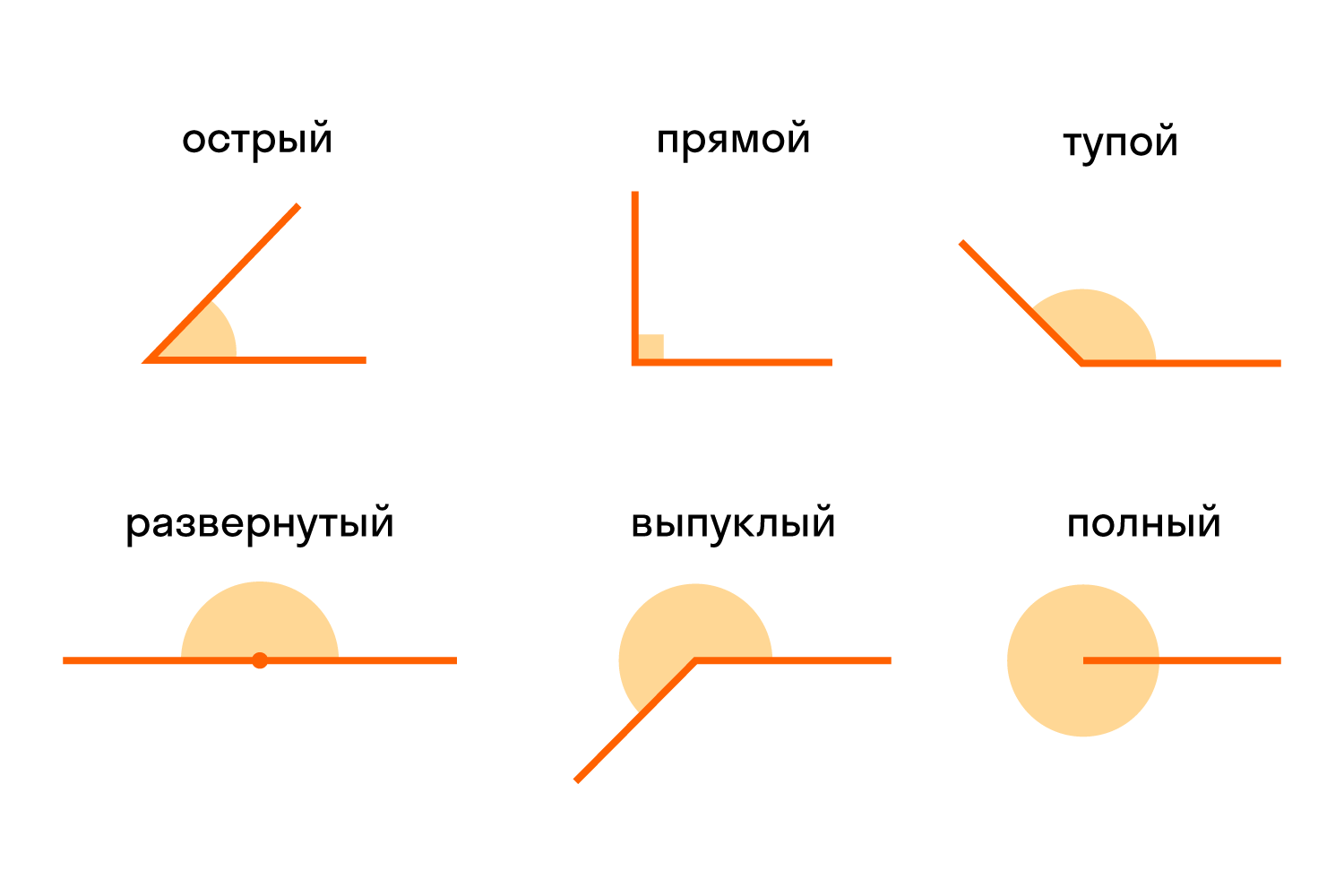
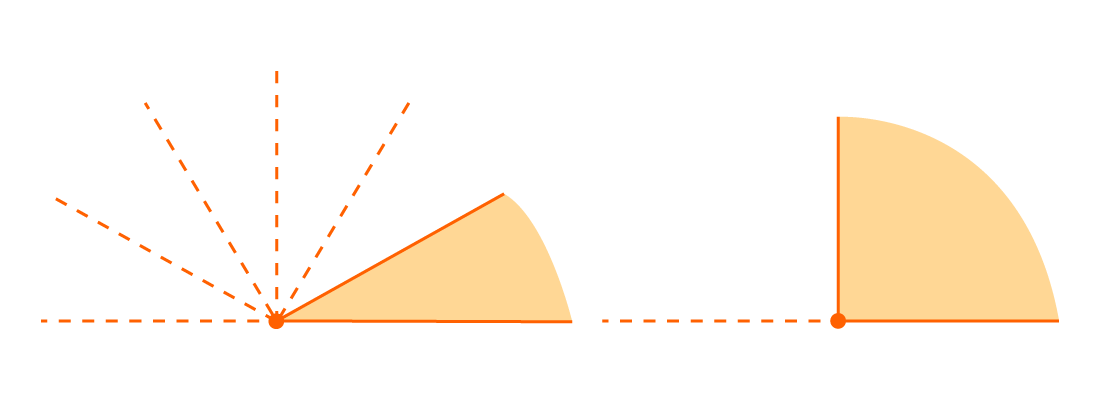
В зависимости от величин, углы бывают следующих типов (Рис.5):

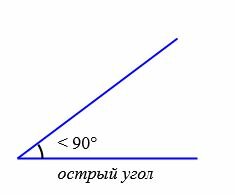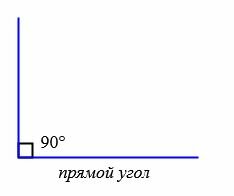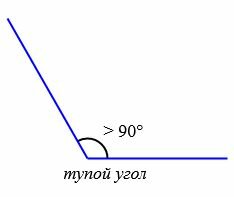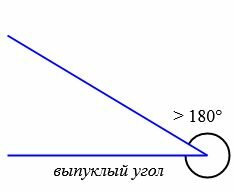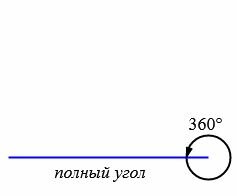Сравнение углов

Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.

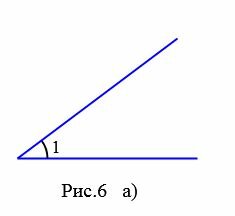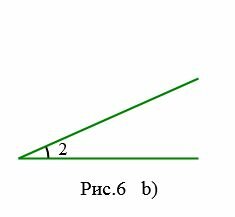На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)

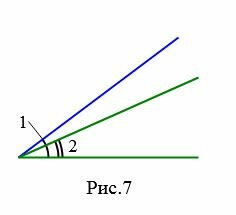Градусная мера угла

Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).

Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)

Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.

Источник

Острый угол

Какой угол называется острым в математике

Угол представляет собой геометрическую фигуру, которая образована с помощью пары лучей. Данные линии называют сторонами. Они берут начало в одной точке, называемой вершиной. Согласно основным признаком геометрической фигуры, можно сформулировать ее понятие.

Угол является геометрической фигурой, состоящей из пары лучей в виде ее сторон, которые выходят из одной точки или вершины.

Данные фигуры в геометрии подразделяют на типы в зависимости от градусной величины, расположению относительно друг друга и относительно окружности. Основными видами являются:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Градусная мера, которой обладает острый угол, менее 90 градусов. Данный вид геометрической фигуры можно встретить в каждом четырехугольнике, если он не является прямоугольным квадратом или произвольным параллелограммом. Острый угол можно полностью вписать во внутреннее пространство прямого, а одна из его сторон является биссектрисой. Пример острого угла АОВ изображен на рисунке:

Определение, основные признаки и свойства

Острый угол – это геометрическая фигура, градусная мера которой составляет менее 90 градусов.

Для всех острых углов характерна градусная мера в интервале от 0 до 90 градусов. Простым способом распознавания типа угла является использование предмета, который имеет прямой угол. Его прикладывают к искомому элементу таким образом, чтобы их вершины были совмещены. Примером такого инструмента является линейка. Возможно два варианта результата измерений:

Точным инструментом для измерения градусной меры является транспортир, который состоит из линейки и полуокружности. Пользоваться им несложно. Достаточно приложить центр транспортира к вершине фигуры таким образом, чтобы любой из его сторон совпадал с гранью линейки. Второй луч покажет градусы, соответствующие геометрической фигуре.

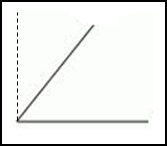
Транспортир также применяют, когда необходимо начертить тупой или острый угол:

Особенности рассматриваемой геометрической фигуры:

Примеры решения задач

Задача 1

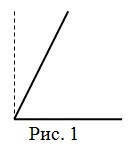
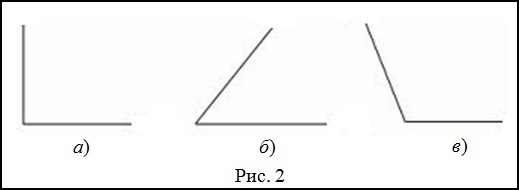
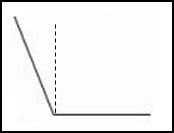
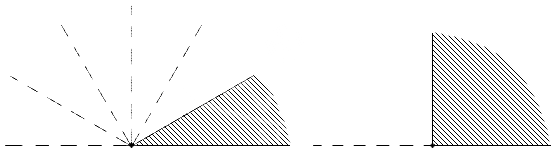
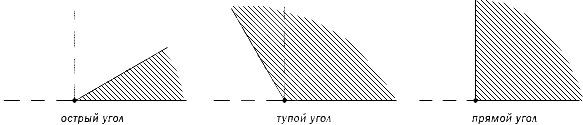
С помощью рисунка необходимо найти острые углы.

Решение

Стороны фигуры, изображенной на первом рисунке, перпендикулярны друг другу. Поэтому его нельзя назвать острым. На втором рисунке начерчен угол, который меньше, чем прямой.

Согласно определению, данный угол является острым. Если сравнить угол, который изображен на третьем рисунке, с прямым, то можно сделать вывод, что он тупой, так как его градусная мера составляет больше, чем 90 градусов.

Ответ: острым является угол, который изображен на втором рисунке.

Задача 2

Имеется пара смежных углов. Один из них больше, чем второй на 30 градусов. Требуется определить, какой из этих углов является острым.

Решение

Обозначим меньший угол буквой х. Тогда (х+30) является большим углом. Известно, что сумма смежных углов составляет 180 градусов. Можно записать справедливое равенство:

Источник

Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

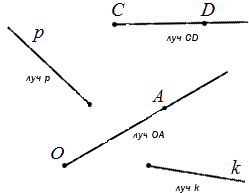
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Внутренняя область угла – элемент, служащий для второго определения угла.

Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.

Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.

Определение смежных и вертикальных углов

Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.

На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.

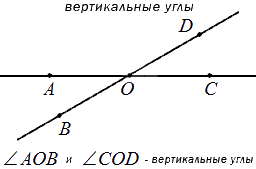
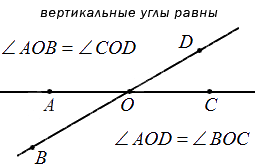
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.

При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.

Сравнение углов

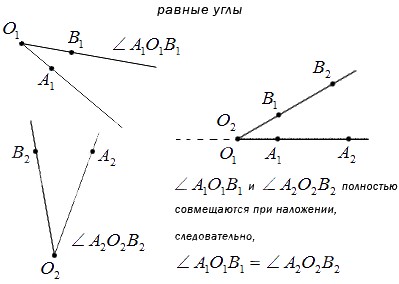
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.

Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.

Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.

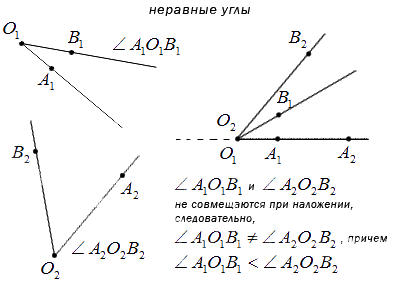
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.

Развернутые углы являются равными.

Измерение углов

Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.

Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.

Чаще всего используют понятие градус.

Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.

Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.

Минутой называют одну шестидесятую часть градуса.

Секундой называют одну шестидесятую часть минуты.

Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « » ». Имеет место обозначение:

Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.

Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.

Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.

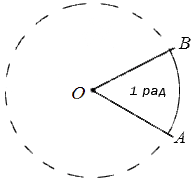
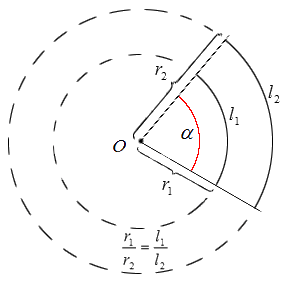
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.

Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.

Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.

На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.

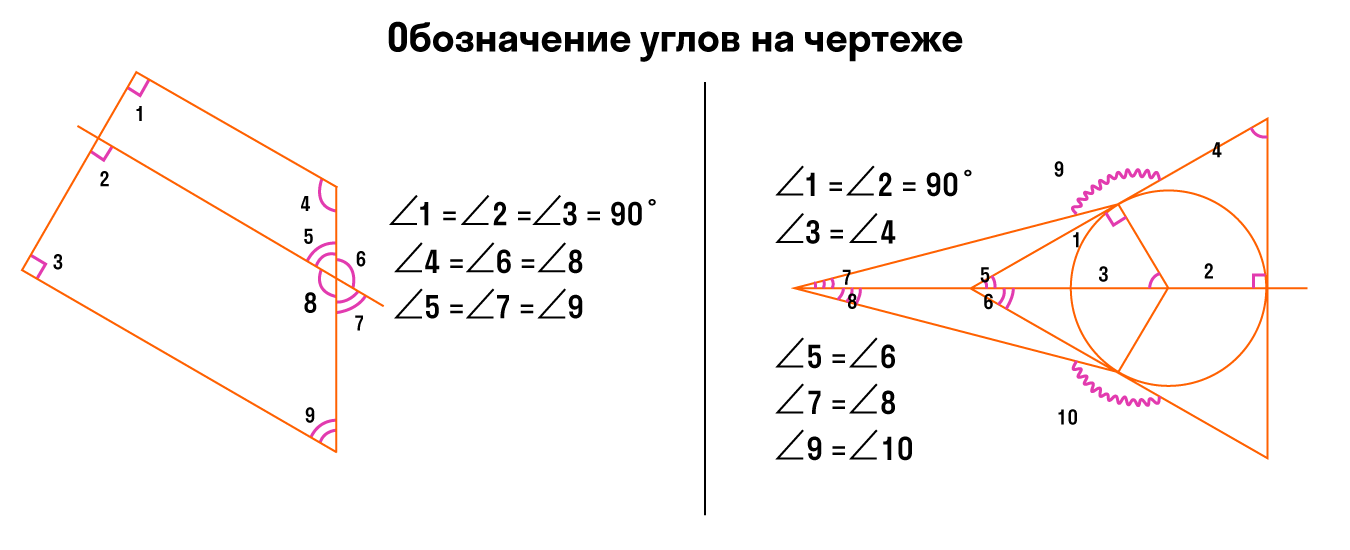
Обозначение углов на чертеже

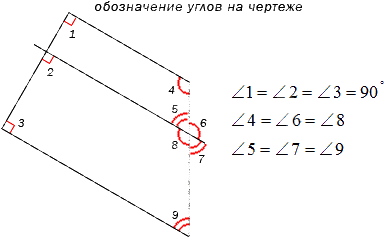
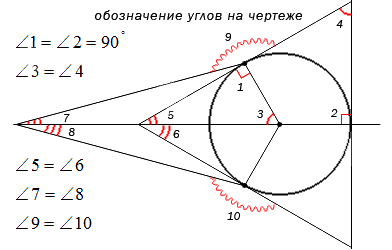
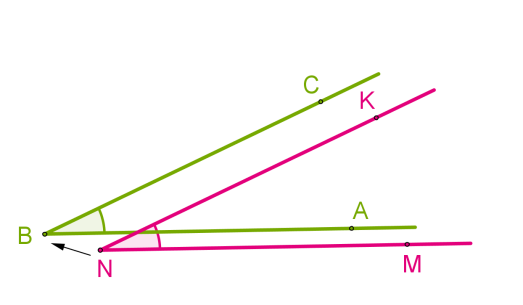
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.

Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.

Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.

Источник

Что такое угол? Виды углов

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

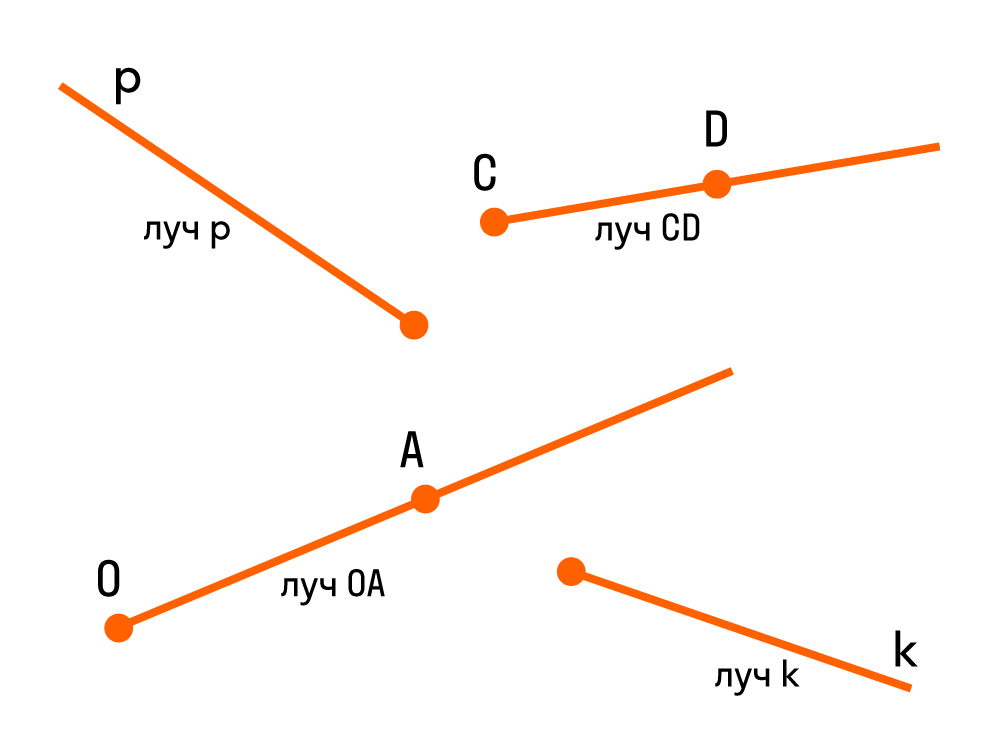
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

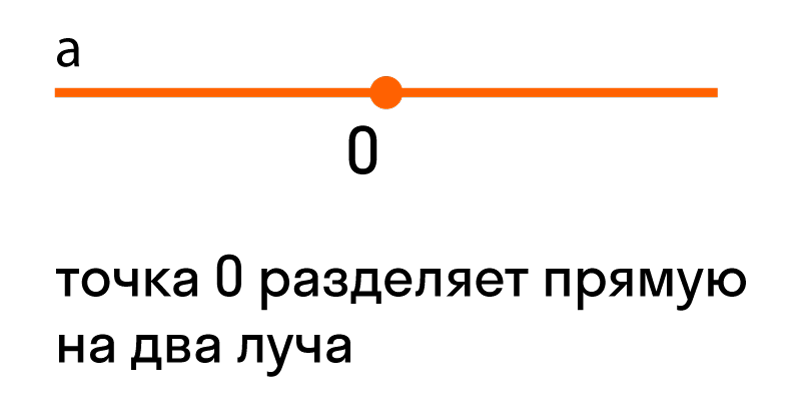
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

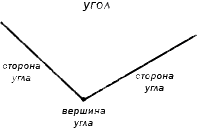
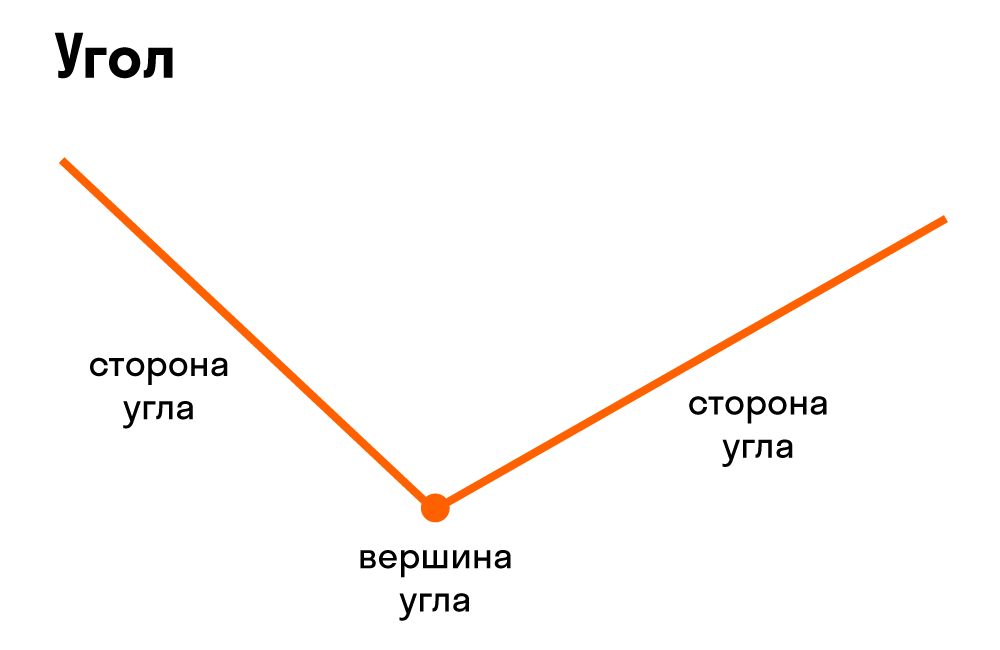
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

Что такое вершина и стороны угла

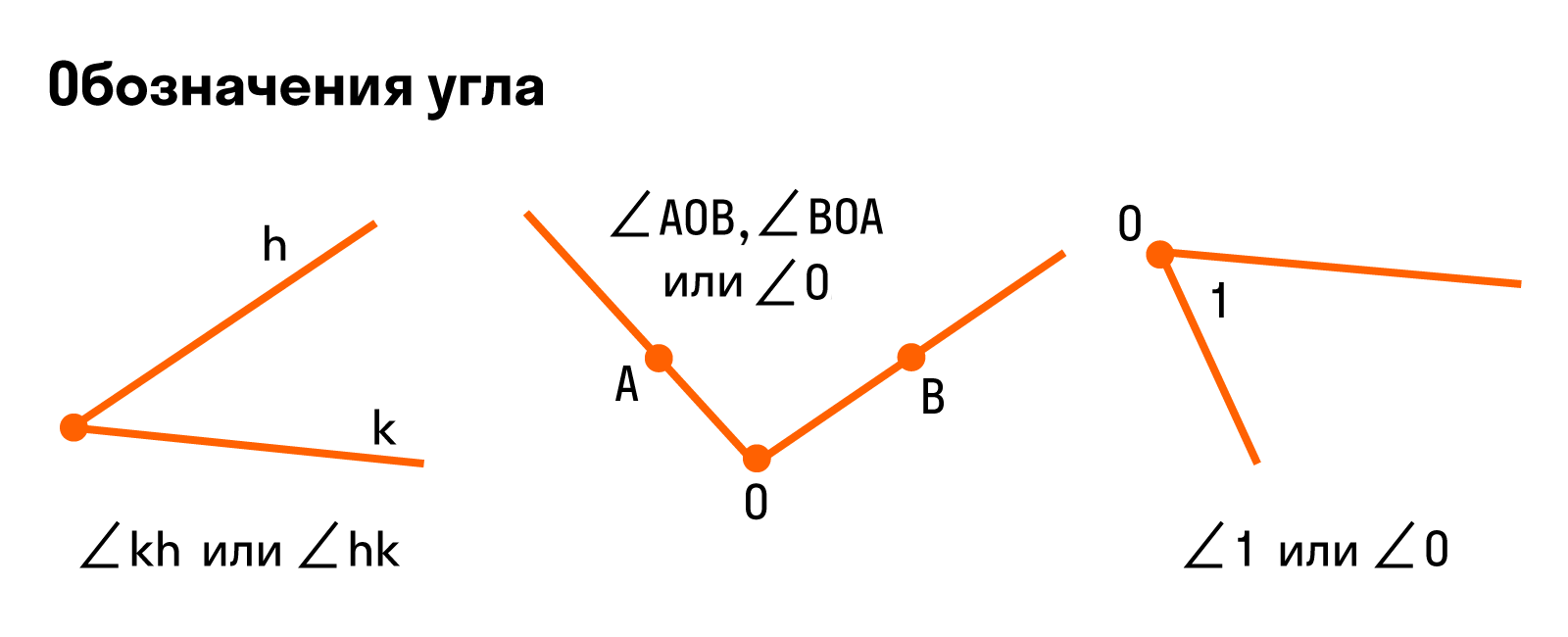
В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

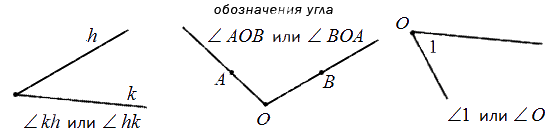
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.

Иногда встречается обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

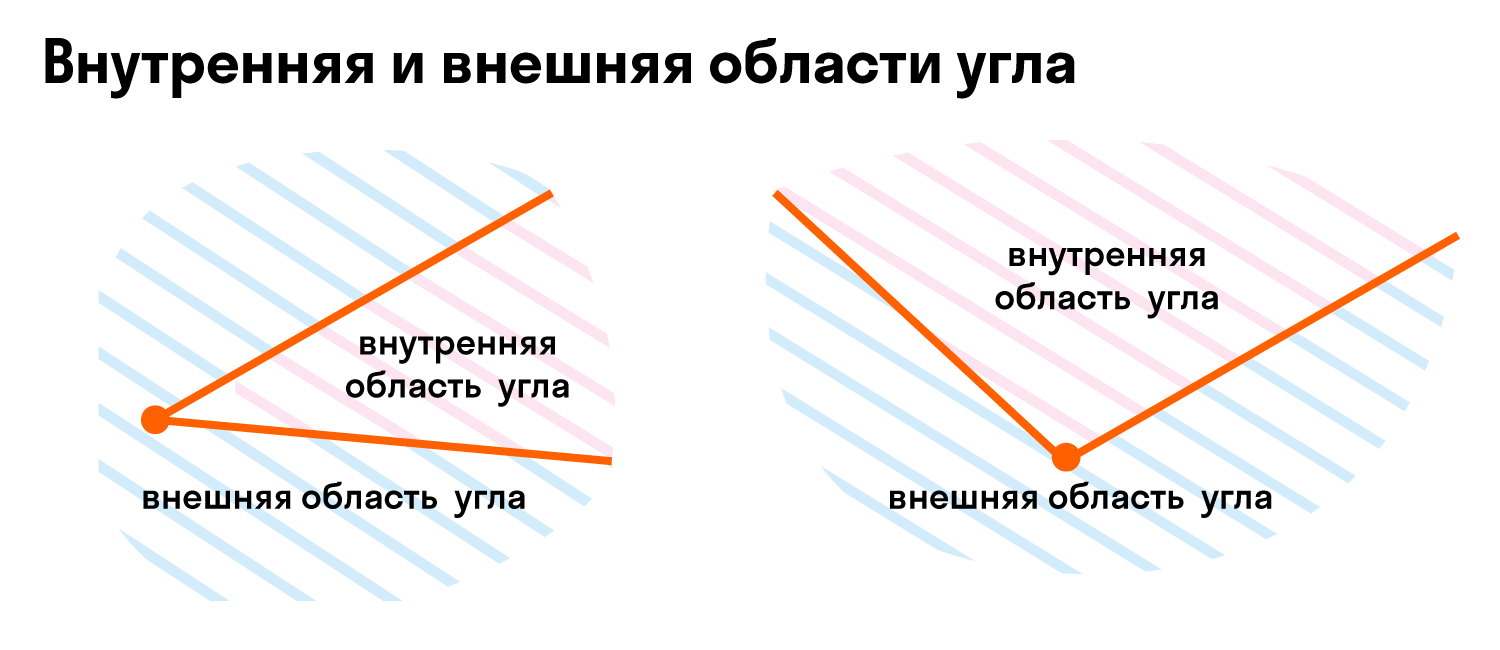
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Виды углов

Есть разные типы углов и у каждого своё название:

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

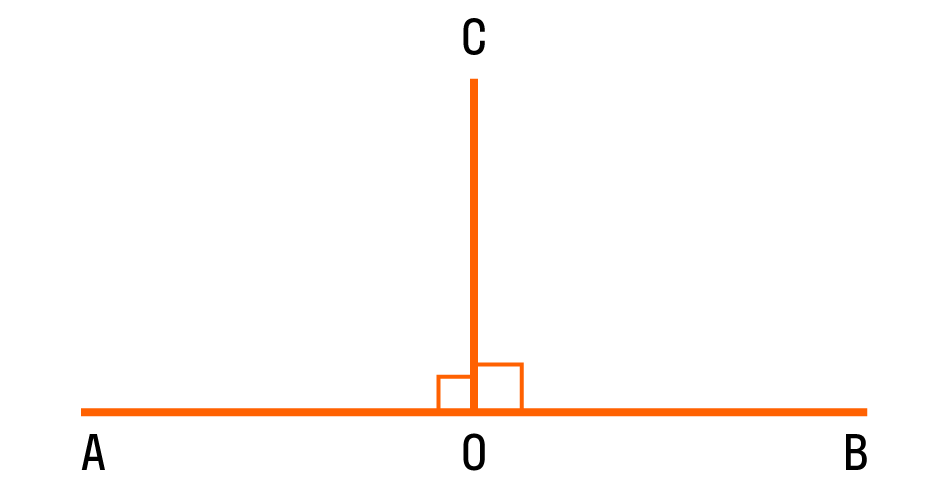
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Острый угол — это угол, который меньше прямого угла, то есть

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

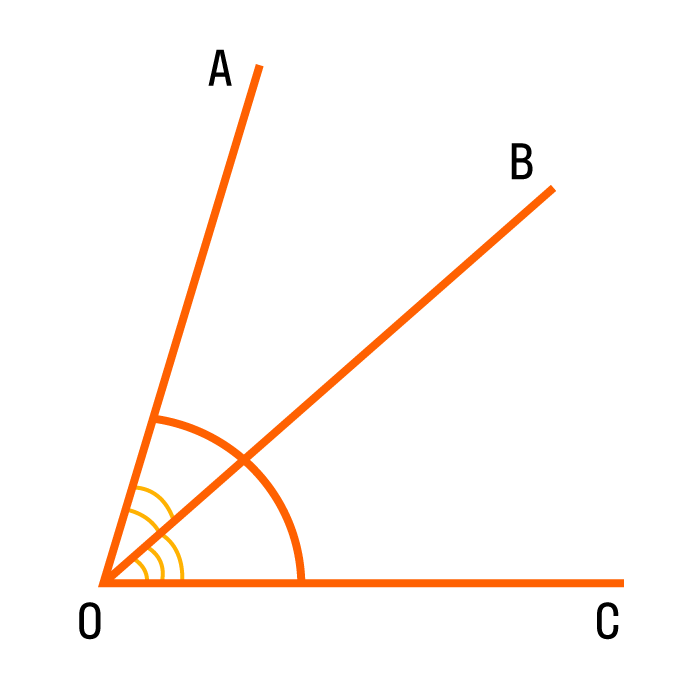
Сравнение углов

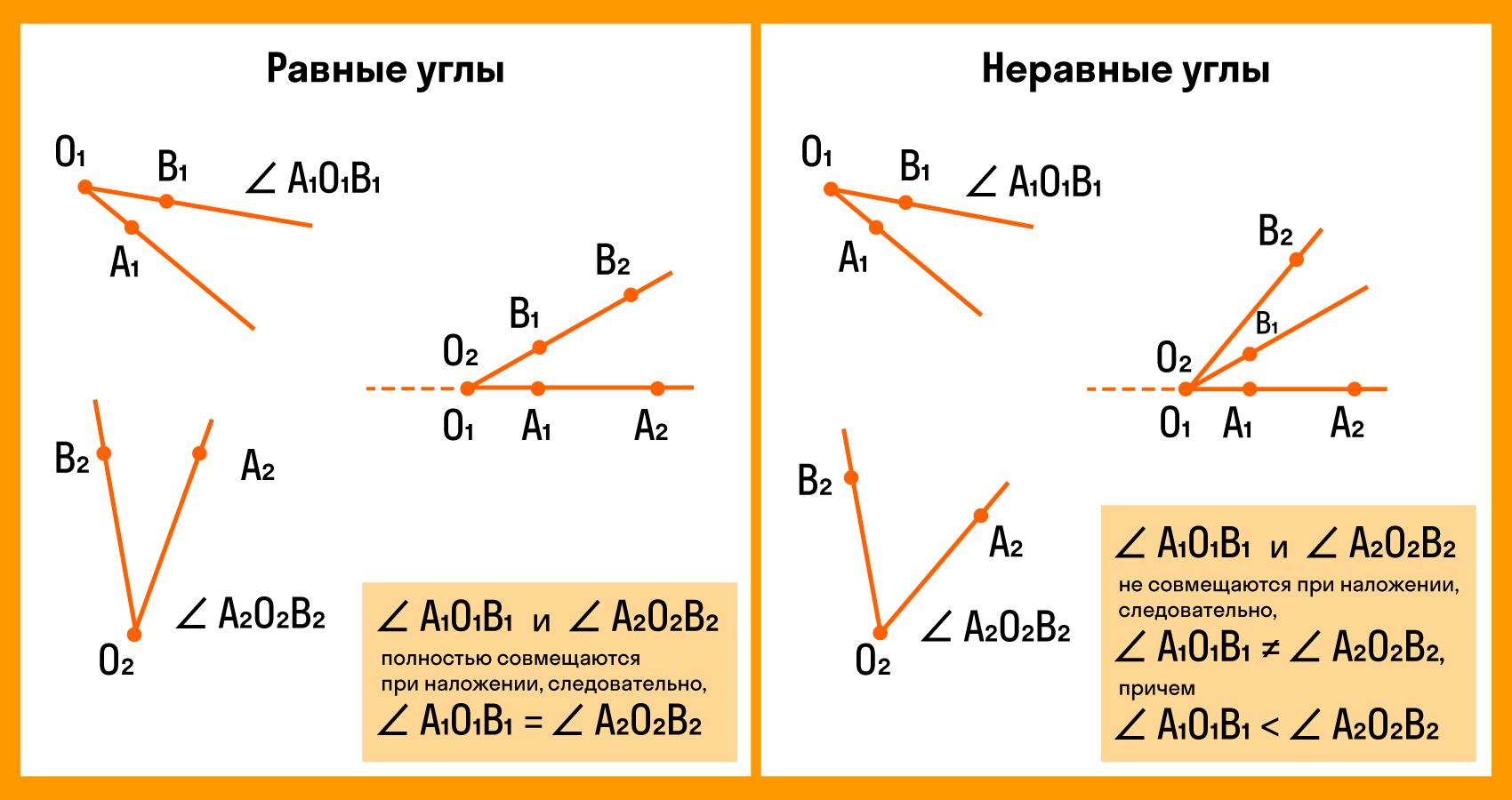
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠??? и ∠??? происходит следующим образом:

Если совпадут и другие стороны, то углы равны: ∠??? = ∠???.

Если нет, то один угол — меньше другого: ∠???

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается ´.

Секунда — 1/60 часть минуты. Обозначается ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.

Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

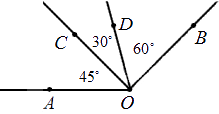
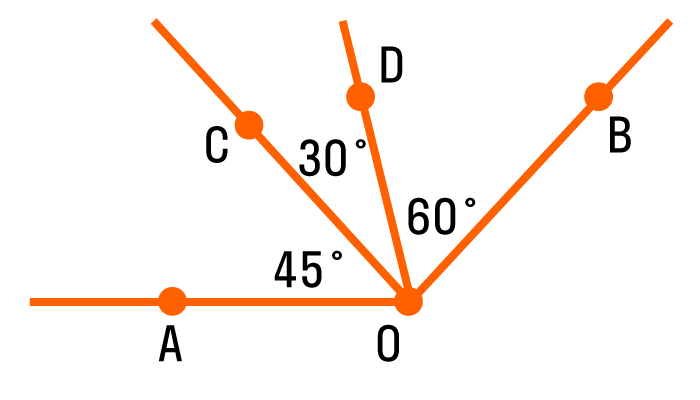
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.

Равные углы имеют равную градусную меру.

Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:

На чертеже отмечены три неравных угла:

Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Источник