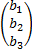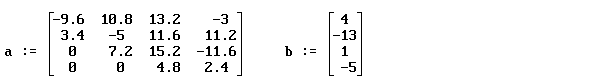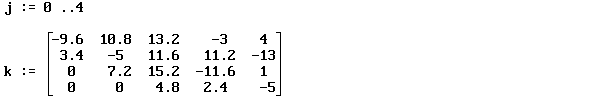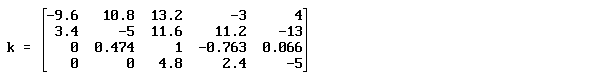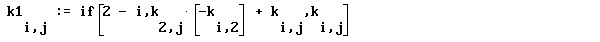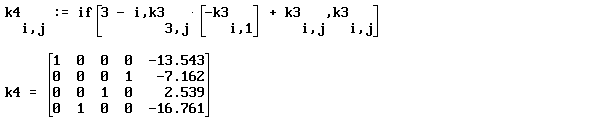Слово Как написать расширенную матрицу - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.

Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.

Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему

Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной, если же решений нет – несовместной. Если совместная СЛАУ имеет ровно одно решение, её именуют определённой, если бесконечное множество решений – неопределённой.

Естественно, возникает вопрос том, является ли проверенное решение единственным. Вопрос о количестве решений СЛАУ будет затронут в соответствующей теме.

$$4x_1+2x_2-x_3=4\cdot 0+2\cdot 0-0=0.$$

Подстановка в иные уравнения делается аналогично.

Матричная форма записи систем линейных алгебраических уравнений.

С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков (см. пример №4).

Чтобы была нагляднее взаимосвязь между матрицей системы и самой системой, я запишу рядом заданную СЛАУ и ее матрицу системы:

Как видите, изменение порядка следования неизвестных равносильно перестановке столбцов матрицы системы. Но каким бы этот порядок расположения неизвестных ни был, он должен совпадать во всех уравнениях заданной СЛАУ.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Система линейных алгебраических уравнений

В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.

Определение системы линейных уравнений

Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:

Индексы коэффициентов ( a_ij ) формируются следующим образом:

Виды СЛАУ

В зависимости от количества решений, СЛАУ может быть:

Матричная форма записи системы

СЛАУ можно представить в матричной форме:

Пример
Представим систему уравнений ниже в матричном виде:

Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.

Полная запись заданной системы уравнений в матричном виде:

Расширенная матрица СЛАУ

Для примера выше получается так:

– обозначение расширенной матрицы.

Источник

Примеры решения СЛАУ

Методы решения систем линейных уравнений широко используются в задачах математики, экономики, физики, химии и других науках. На практике, они позволяют не делать лишних действий, а записать систему уравнений в более компактной форме и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять основные методы решения и научиться выбирать оптимальный.

Перед изучением примеров решения задач советуем изучить теоретический материал по СЛАУ, прочитать все теоремы и методы решения. Список тем находится в правом меню.

Примеры по темам:

СЛАУ: основные понятия, виды

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Примеры решения СЛАУ не по зубам? Тебе ответит эксперт через 10 минут!

вектор-столбец свободных коэффициентов:

то есть, запись СЛАУ в матричной форме:

Критерий совместности системы

и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от второй строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:

Третью строку складываем с первой:

и меняем первую и вторую строки матрицы местами

Квадратные СЛАУ. Матричный метод решения

Решение. Запишем данную систему в матричной форме:

Отсюда искомая матрица

Метод / Теорема Крамера

Решение. Вычисляем определитель матрицы системы:

$$\Delta=\left|\begin 5 & 2 \\ 2 & 1 \end\right|=5 \cdot 1-2 \cdot 2=1 \neq 0$$

$$\Delta_<1>=\left|\begin 7 & 2 \\ 9 & 1 \end\right|=7-18=-11$$

$$\Delta_<2>=\left|\begin 5 & 7 \\ 2 & 9 \end\right|=45-14=31$$

Тогда получаем, что

Решение. Вычисляем определитель матрицы системы:

Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:

Метод Гаусса. Метод последовательного исключения неизвестных

Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

От третьей строки отнимаем вторую, умноженную на 3:

Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:

Полученной матрице соответствует система

Однородные СЛАУ. Фундаментальная система решений

Решение. Вычислим определитель матрицы системы:

Ответ. Система имеет только нулевое решение.

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

Нулевые строки можно далее не рассматривать, тогда получаем, что

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

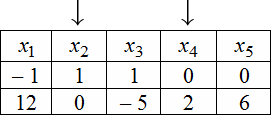
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

Общее решение является линейной комбинацией частных решений:

Источник

Расширенная матрица СЛАУ. Элементарные преобразования расширенной матрицы СЛАУ.

Расширенная матрица СЛАУ:

[A_B] – расширенная матрица-система

А= X= B=

А_В =

Элементарные преобразования расширенной матрицы СЛАУ:

1 – перемены местами любых столбцов матрицы А и любых строк расширенной матрицы А_В всегда допустимо.

2 – можно удалять нулевые строки, одну из одинаковых строк, и строки, элементы которых пропорциональны.

3 – любую строку расширенной матрицы А_В можно умножить на отличное от 0 число.

4 – допустимо прибавлять к элементам строки элементы другой строки, умноженные на произвольное число.

Вопрос №11
Метод Гаусса для решения СЛАУ.

Метод Гаусса – метод последовательного исключения переменных, заключающийся в том, что с помощью элементарных преобразований система приводится к ступенчатому виду, из которой по порядку, начиная с самого последнего номера, находятся все переменные.

При решении системы методом Гаусса выполняется прямой и обратный ход, а затем следует проверка:

1) При прямом ходе: расширенная матрица-система приводится к ступенчатому виду;

2) При обратном ходе последовательно находятся переменные;

Вопрос №12

Ранг матрицы. Теорема Кронекера-Капелли.

Ранг матрицы:

Рангом произвольной матрицы А, приведенной к каноническому виду, называется минимальное число из не нулевых строк или столбцов.

где m – кол-во ненулевых строк, n – кол-во ненулевых столбцов.

Теорема Кронекера-Капелли:

Система уравнений является совместной тогда и только тогда, когда ранг расширенной матрицы А_В равен рангу матрицы А.

1. Если ранг матрицы А (Rang A) = числу совместных неизвестных переменных, то система определенная

Если длина вектора =0, то он называется нулевым. Его направление можно считать произвольным.

Вектор «–а» можно считать противоположным вектором для вектора «а», если он имеет такую же длину, но противоположное направление.

Модуль – длина вектора.

Если 2 вектора лежат на 1 прямой или на параллельных прямых, то они называются коллинеарными.

Вектора называются компланарными, если они лежат на 1 плоскости или на параллельных плоскостях.

Источник

Пример. Записывается расширенная матрица

Записывается расширенная матрица

В матрице a выбирается максимальный по модулю элемент, который называется главным. На этот элемент делится строка расширенной матрицы, содержащая главный элемент.

Полученный результат записывается в матрицу k.

Из каждой строки матрицы k вычитается строка, содержащая главный элемент, умноженная на элемент, стоящий на пересечении текущей строки и столбца, содержащего главный элемент.

В результате коэффициенты при 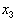обращаются в нуль.

Дальнейшие вычисления производятся аналогично.

В результате получается расширенная матрица, состоящая из единичной матрицы и вектора-столбца.

Вектор-столбец является решением исходной системы.

Решение системы линейных уравнений можно найти, используя операторы пакета для работы с матрицами.

1.3. Итерационные методы решения систем уравнений

1.3.1. Решение систем линейных алгебраических уравнений методом Зейделя.

Тема: Решение системы линейных уравнений методом Зейделя с точностью .

Источник